Optimizing Shortfall Risk Metric for Learning Regression Models

We consider the problem of estimating and optimizing utility-based shortfall risk (UBSR) of a loss, say $(Y - \hat Y)^2$, in the context of a regression problem. Empirical risk minimization with a UBSR objective is challenging since UBSR is a non-linear function of the underlying distribution. We first derive a concentration bound for UBSR estimation using independent and identically distributed (i.i.d.) samples. We then frame the UBSR optimization problem as minimization of a pseudo-linear function in the space of achievable distributions $\mathcal D$ of the loss $(Y- \hat Y)^2$. We construct a gradient oracle for the UBSR objective and a linear minimization oracle (LMO) for the set $\mathcal D$. Using these oracles, we devise a bisection-type algorithm, and establish convergence to the UBSR-optimal solution.

Concentration Bounds for Optimized Certainty Equivalent Risk Estimation

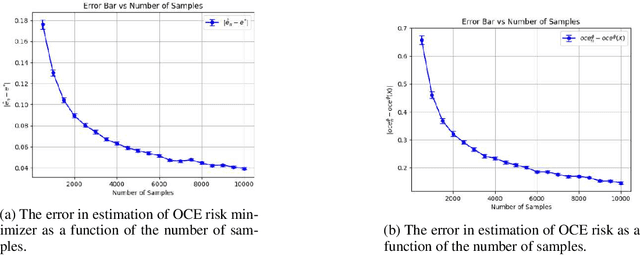
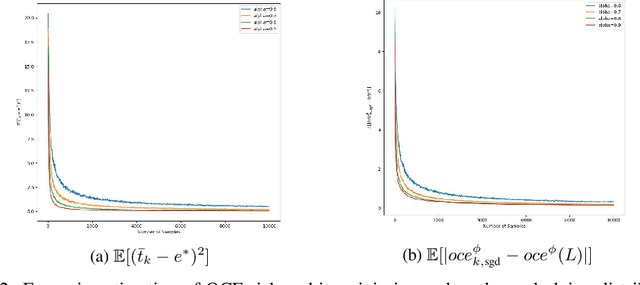
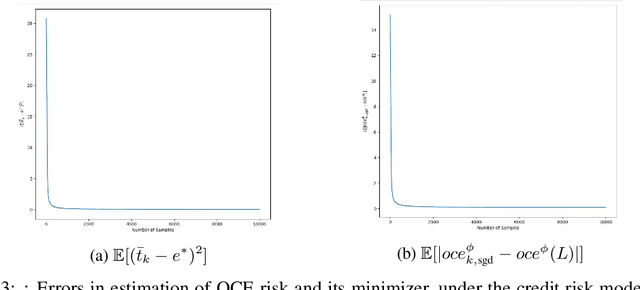
We consider the problem of estimating the Optimized Certainty Equivalent (OCE) risk from independent and identically distributed (i.i.d.) samples. For the classic sample average approximation (SAA) of OCE, we derive mean-squared error as well as concentration bounds (assuming sub-Gaussianity). Further, we analyze an efficient stochastic approximation-based OCE estimator, and derive finite sample bounds for the same. To show the applicability of our bounds, we consider a risk-aware bandit problem, with OCE as the risk. For this problem, we derive bound on the probability of mis-identification. Finally, we conduct numerical experiments to validate the theoretical findings.

Stochastic approximation for speeding up LSTD (and LSPI)

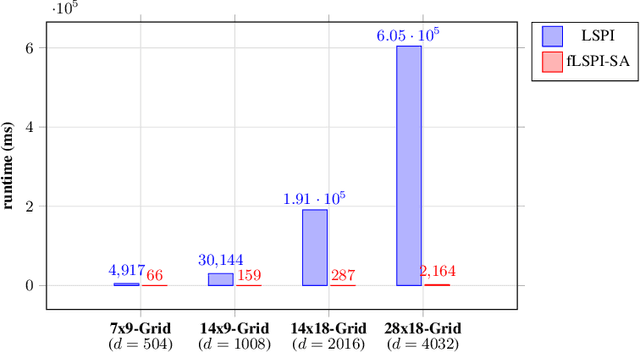
We propose a stochastic approximation (SA) based method with randomization of samples for policy evaluation using the least squares temporal difference (LSTD) algorithm. Our method results in an $O(d)$ improvement in complexity in comparison to regular LSTD, where $d$ is the dimension of the data. We provide convergence rate results for our proposed method, both in high probability and in expectation. Moreover, we also establish that using our scheme in place of LSTD does not impact the rate of convergence of the approximate value function to the true value function and hence a low-complexity LSPI variant that uses our SA based scheme has the same order of the performance bounds as that of regular LSPI. These rate results coupled with the low complexity of our method make it attractive for implementation in big data settings, where $d$ is large. Furthermore, we analyze a similar low-complexity alternative for least squares regression and provide finite-time bounds there. We demonstrate the practicality of our method for LSTD empirically by combining it with the LSPI algorithm in a traffic signal control application. We also conduct another set of experiments that combines the SA based low-complexity variant for least squares regression with the LinUCB algorithm for contextual bandits, using the large scale news recommendation dataset from Yahoo.

Weighted bandits or: How bandits learn distorted values that are not expected

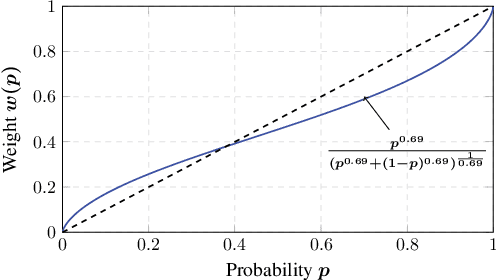
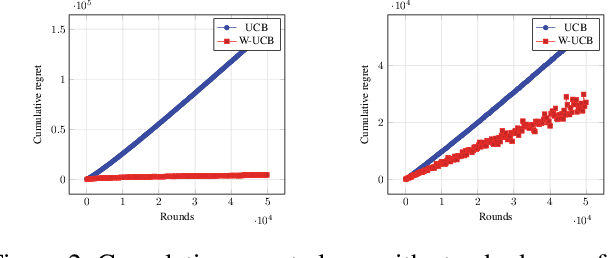
Motivated by models of human decision making proposed to explain commonly observed deviations from conventional expected value preferences, we formulate two stochastic multi-armed bandit problems with distorted probabilities on the cost distributions: the classic $K$-armed bandit and the linearly parameterized bandit. In both settings, we propose algorithms that are inspired by Upper Confidence Bound (UCB), incorporate cost distortions, and exhibit sublinear regret assuming \holder continuous weight distortion functions. For the $K$-armed setting, we show that the algorithm, called W-UCB, achieves problem-dependent regret $O(L^2 M^2 \log n/ \Delta^{\frac{2}{\alpha}-1})$, where $n$ is the number of plays, $\Delta$ is the gap in distorted expected value between the best and next best arm, $L$ and $\alpha$ are the H\"{o}lder constants for the distortion function, and $M$ is an upper bound on costs, and a problem-independent regret bound of $O((KL^2M^2)^{\alpha/2}n^{(2-\alpha)/2})$. We also present a matching lower bound on the regret, showing that the regret of W-UCB is essentially unimprovable over the class of H\"{o}lder-continuous weight distortions. For the linearly parameterized setting, we develop a new algorithm, a variant of the Optimism in the Face of Uncertainty Linear bandit (OFUL) algorithm called WOFUL (Weight-distorted OFUL), and show that it has regret $O(d\sqrt{n} \; \mbox{polylog}(n))$ with high probability, for sub-Gaussian cost distributions. Finally, numerical examples demonstrate the advantages resulting from using distortion-aware learning algorithms.

On TD(0) with function approximation: Concentration bounds and a centered variant with exponential convergence

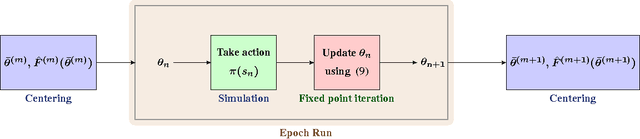
We provide non-asymptotic bounds for the well-known temporal difference learning algorithm TD(0) with linear function approximators. These include high-probability bounds as well as bounds in expectation. Our analysis suggests that a step-size inversely proportional to the number of iterations cannot guarantee optimal rate of convergence unless we assume (partial) knowledge of the stationary distribution for the Markov chain underlying the policy considered. We also provide bounds for the iterate averaged TD(0) variant, which gets rid of the step-size dependency while exhibiting the optimal rate of convergence. Furthermore, we propose a variant of TD(0) with linear approximators that incorporates a centering sequence, and establish that it exhibits an exponential rate of convergence in expectation. We demonstrate the usefulness of our bounds on two synthetic experimental settings.

Actor-Critic Algorithms for Learning Nash Equilibria in N-player General-Sum Games

We consider the problem of finding stationary Nash equilibria (NE) in a finite discounted general-sum stochastic game. We first generalize a non-linear optimization problem from Filar and Vrieze [2004] to a $N$-player setting and break down this problem into simpler sub-problems that ensure there is no Bellman error for a given state and an agent. We then provide a characterization of solution points of these sub-problems that correspond to Nash equilibria of the underlying game and for this purpose, we derive a set of necessary and sufficient SG-SP (Stochastic Game - Sub-Problem) conditions. Using these conditions, we develop two actor-critic algorithms: OFF-SGSP (model-based) and ON-SGSP (model-free). Both algorithms use a critic that estimates the value function for a fixed policy and an actor that performs descent in the policy space using a descent direction that avoids local minima. We establish that both algorithms converge, in self-play, to the equilibria of a certain ordinary differential equation (ODE), whose stable limit points coincide with stationary NE of the underlying general-sum stochastic game. On a single state non-generic game (see Hart and Mas-Colell [2005]) as well as on a synthetic two-player game setup with $810,000$ states, we establish that ON-SGSP consistently outperforms NashQ ([Hu and Wellman, 2003] and FFQ [Littman, 2001] algorithms.

Simultaneous Perturbation Algorithms for Batch Off-Policy Search

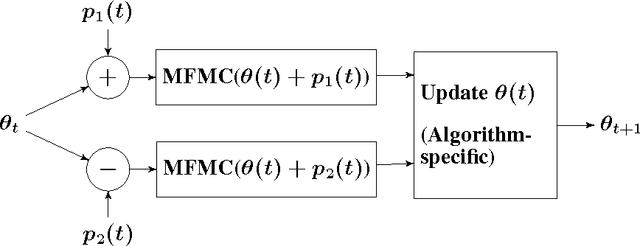
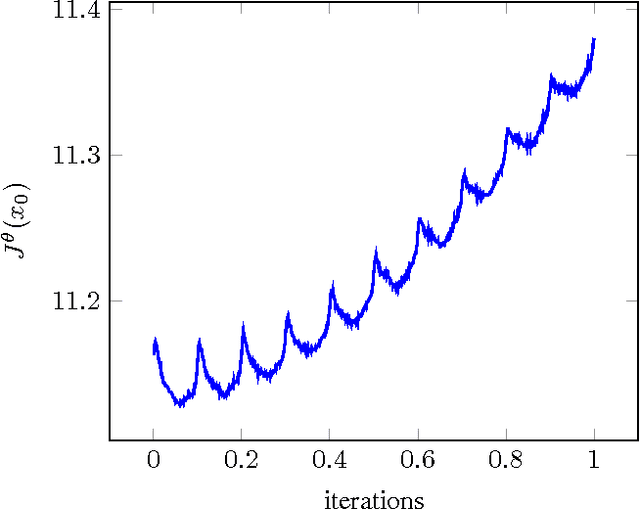
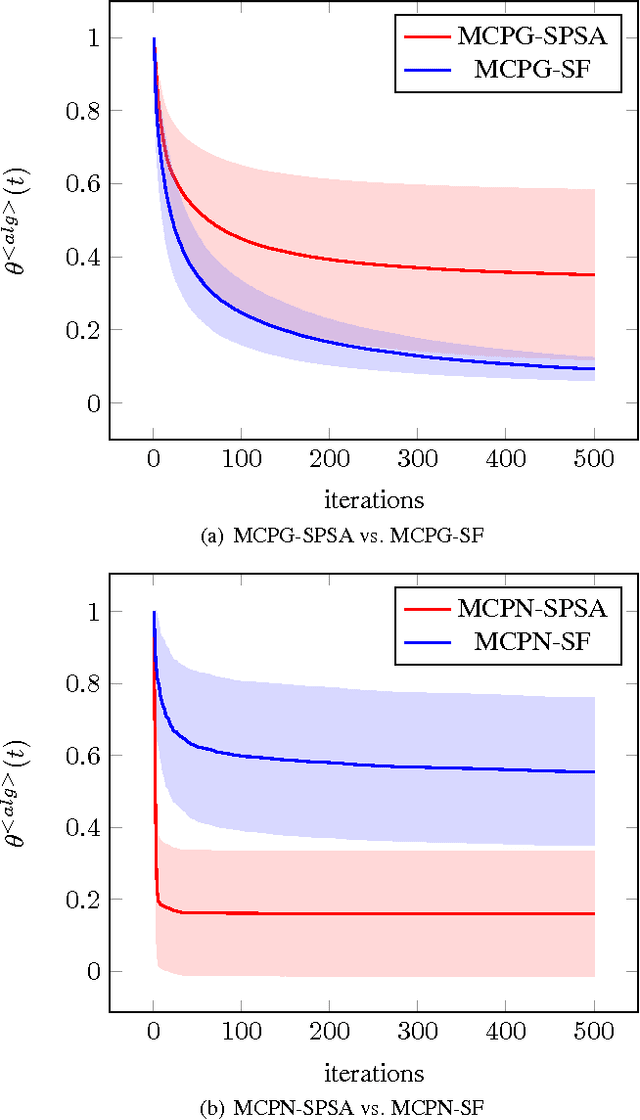
We propose novel policy search algorithms in the context of off-policy, batch mode reinforcement learning (RL) with continuous state and action spaces. Given a batch collection of trajectories, we perform off-line policy evaluation using an algorithm similar to that by [Fonteneau et al., 2010]. Using this Monte-Carlo like policy evaluator, we perform policy search in a class of parameterized policies. We propose both first order policy gradient and second order policy Newton algorithms. All our algorithms incorporate simultaneous perturbation estimates for the gradient as well as the Hessian of the cost-to-go vector, since the latter is unknown and only biased estimates are available. We demonstrate their practicality on a simple 1-dimensional continuous state space problem.