AI for DevSecOps: A Landscape and Future Opportunities

DevOps has emerged as one of the most rapidly evolving software development paradigms. With the growing concerns surrounding security in software systems, the DevSecOps paradigm has gained prominence, urging practitioners to incorporate security practices seamlessly into the DevOps workflow. However, integrating security into the DevOps workflow can impact agility and impede delivery speed. Recently, the advancement of artificial intelligence (AI) has revolutionized automation in various software domains, including software security. AI-driven security approaches, particularly those leveraging machine learning or deep learning, hold promise in automating security workflows. They reduce manual efforts, which can be integrated into DevOps to ensure uninterrupted delivery speed and align with the DevSecOps paradigm simultaneously. This paper seeks to contribute to the critical intersection of AI and DevSecOps by presenting a comprehensive landscape of AI-driven security techniques applicable to DevOps and identifying avenues for enhancing security, trust, and efficiency in software development processes. We analyzed 99 research papers spanning from 2017 to 2023. Specifically, we address two key research questions (RQs). In RQ1, we identified 12 security tasks associated with the DevOps process and reviewed existing AI-driven security approaches. In RQ2, we discovered 15 challenges encountered by existing AI-driven security approaches and derived future research opportunities. Drawing insights from our findings, we discussed the state-of-the-art AI-driven security approaches, highlighted challenges in existing research, and proposed avenues for future opportunities.

Learning to Quantize Vulnerability Patterns and Match to Locate Statement-Level Vulnerabilities

Deep learning (DL) models have become increasingly popular in identifying software vulnerabilities. Prior studies found that vulnerabilities across different vulnerable programs may exhibit similar vulnerable scopes, implicitly forming discernible vulnerability patterns that can be learned by DL models through supervised training. However, vulnerable scopes still manifest in various spatial locations and formats within a program, posing challenges for models to accurately identify vulnerable statements. Despite this challenge, state-of-the-art vulnerability detection approaches fail to exploit the vulnerability patterns that arise in vulnerable programs. To take full advantage of vulnerability patterns and unleash the ability of DL models, we propose a novel vulnerability-matching approach in this paper, drawing inspiration from program analysis tools that locate vulnerabilities based on pre-defined patterns. Specifically, a vulnerability codebook is learned, which consists of quantized vectors representing various vulnerability patterns. During inference, the codebook is iterated to match all learned patterns and predict the presence of potential vulnerabilities within a given program. Our approach was extensively evaluated on a real-world dataset comprising more than 188,000 C/C++ functions. The evaluation results show that our approach achieves an F1-score of 94% (6% higher than the previous best) and 82% (19% higher than the previous best) for function and statement-level vulnerability identification, respectively. These substantial enhancements highlight the effectiveness of our approach to identifying vulnerabilities. The training code and pre-trained models are available at https://github.com/optimatch/optimatch.

FeatherNets: Convolutional Neural Networks as Light as Feather for Face Anti-spoofing

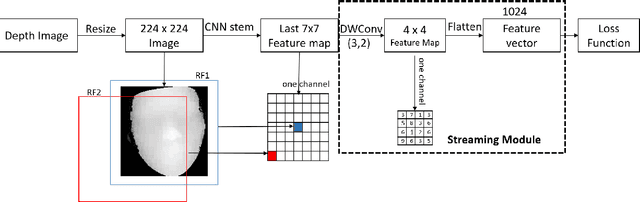
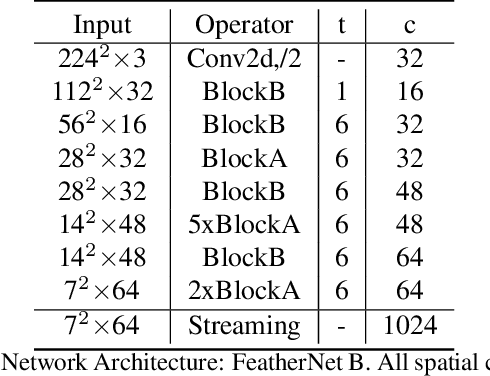
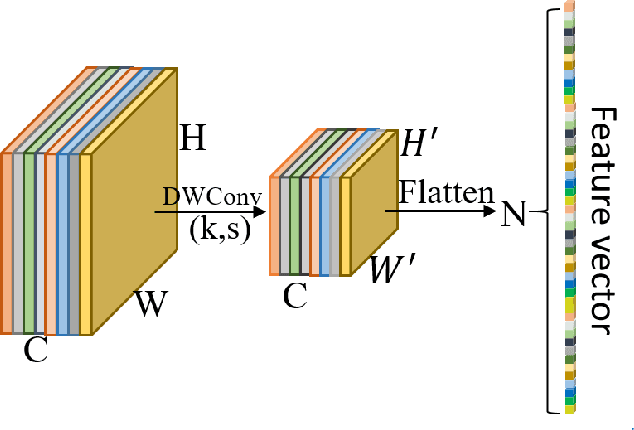
Face Anti-spoofing gains increased attentions recently in both academic and industrial fields. With the emergence of various CNN based solutions, the multi-modal(RGB, depth and IR) methods based CNN showed better performance than single modal classifiers. However, there is a need for improving the performance and reducing the complexity. Therefore, an extreme light network architecture(FeatherNet A/B) is proposed with a streaming module which fixes the weakness of Global Average Pooling and uses less parameters. Our single FeatherNet trained by depth image only, provides a higher baseline with 0.00168 ACER, 0.35M parameters and 83M FLOPS. Furthermore, a novel fusion procedure with ``ensemble + cascade'' structure is presented to satisfy the performance preferred use cases. Meanwhile, the MMFD dataset is collected to provide more attacks and diversity to gain better generalization. We use the fusion method in the Face Anti-spoofing Attack Detection Challenge@CVPR2019 and got the result of 0.0013(ACER), 0.999(TPR@FPR=10e-2), 0.998(TPR@FPR=10e-3) and 0.9814(TPR@FPR=10e-4).

Risk-Sensitive Reinforcement Learning: A Constrained Optimization Viewpoint

The classic objective in a reinforcement learning (RL) problem is to find a policy that minimizes, in expectation, a long-run objective such as the infinite-horizon discounted or long-run average cost. In many practical applications, optimizing the expected value alone is not sufficient, and it may be necessary to include a risk measure in the optimization process, either as the objective or as a constraint. Various risk measures have been proposed in the literature, e.g., mean-variance tradeoff, exponential utility, the percentile performance, value at risk, conditional value at risk, prospect theory and its later enhancement, cumulative prospect theory. In this article, we focus on the combination of risk criteria and reinforcement learning in a constrained optimization framework, i.e., a setting where the goal to find a policy that optimizes the usual objective of infinite-horizon discounted/average cost, while ensuring that an explicit risk constraint is satisfied. We introduce the risk-constrained RL framework, cover popular risk measures based on variance, conditional value-at-risk and cumulative prospect theory, and present a template for a risk-sensitive RL algorithm. We survey some of our recent work on this topic, covering problems encompassing discounted cost, average cost, and stochastic shortest path settings, together with the aforementioned risk measures in a constrained framework. This non-exhaustive survey is aimed at giving a flavor of the challenges involved in solving a risk-sensitive RL problem, and outlining some potential future research directions.

Random directions stochastic approximation with deterministic perturbations

We introduce deterministic perturbation schemes for the recently proposed random directions stochastic approximation (RDSA) [17], and propose new first-order and second-order algorithms. In the latter case, these are the first second-order algorithms to incorporate deterministic perturbations. We show that the gradient and/or Hessian estimates in the resulting algorithms with deterministic perturbations are asymptotically unbiased, so that the algorithms are provably convergent. Furthermore, we derive convergence rates to establish the superiority of the first-order and second-order algorithms, for the special case of a convex and quadratic optimization problem, respectively. Numerical experiments are used to validate the theoretical results.

Weighted bandits or: How bandits learn distorted values that are not expected

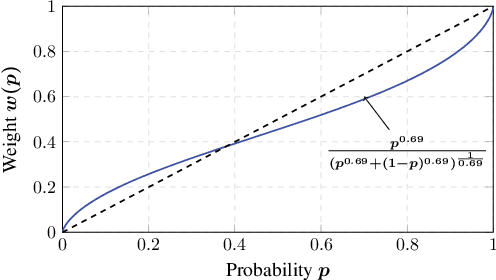
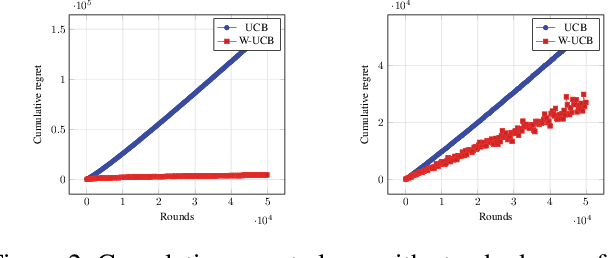
Motivated by models of human decision making proposed to explain commonly observed deviations from conventional expected value preferences, we formulate two stochastic multi-armed bandit problems with distorted probabilities on the cost distributions: the classic $K$-armed bandit and the linearly parameterized bandit. In both settings, we propose algorithms that are inspired by Upper Confidence Bound (UCB), incorporate cost distortions, and exhibit sublinear regret assuming \holder continuous weight distortion functions. For the $K$-armed setting, we show that the algorithm, called W-UCB, achieves problem-dependent regret $O(L^2 M^2 \log n/ \Delta^{\frac{2}{\alpha}-1})$, where $n$ is the number of plays, $\Delta$ is the gap in distorted expected value between the best and next best arm, $L$ and $\alpha$ are the H\"{o}lder constants for the distortion function, and $M$ is an upper bound on costs, and a problem-independent regret bound of $O((KL^2M^2)^{\alpha/2}n^{(2-\alpha)/2})$. We also present a matching lower bound on the regret, showing that the regret of W-UCB is essentially unimprovable over the class of H\"{o}lder-continuous weight distortions. For the linearly parameterized setting, we develop a new algorithm, a variant of the Optimism in the Face of Uncertainty Linear bandit (OFUL) algorithm called WOFUL (Weight-distorted OFUL), and show that it has regret $O(d\sqrt{n} \; \mbox{polylog}(n))$ with high probability, for sub-Gaussian cost distributions. Finally, numerical examples demonstrate the advantages resulting from using distortion-aware learning algorithms.

Cumulative Prospect Theory Meets Reinforcement Learning: Prediction and Control

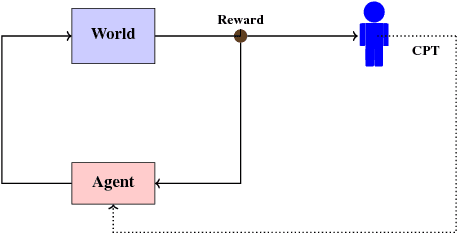
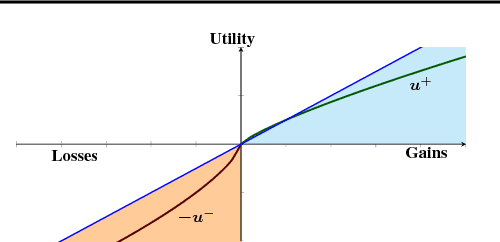
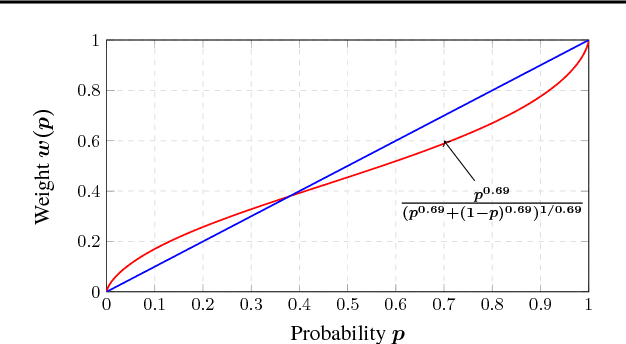
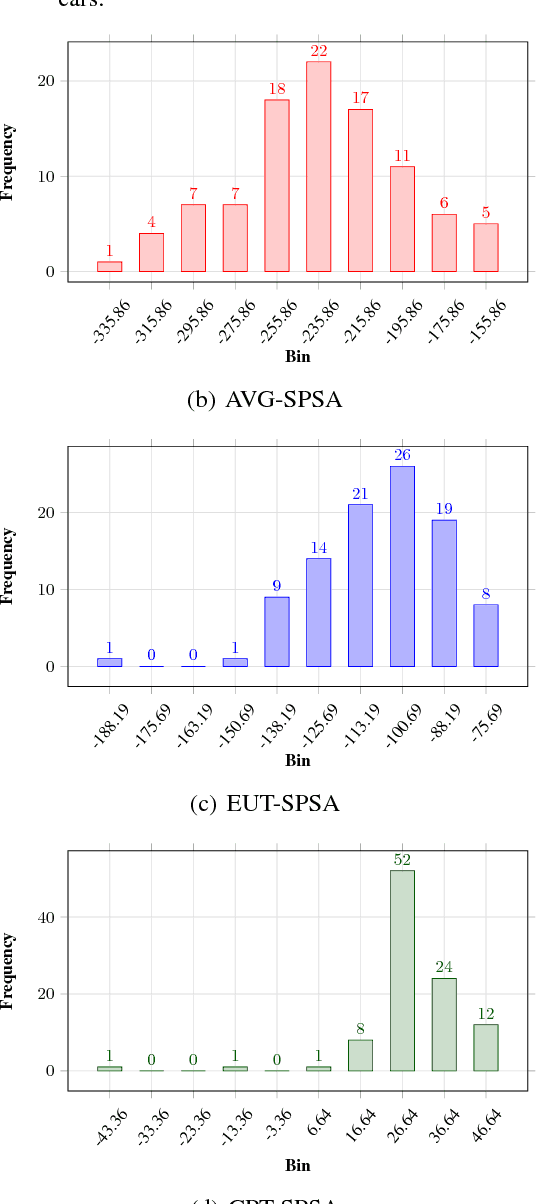
Cumulative prospect theory (CPT) is known to model human decisions well, with substantial empirical evidence supporting this claim. CPT works by distorting probabilities and is more general than the classic expected utility and coherent risk measures. We bring this idea to a risk-sensitive reinforcement learning (RL) setting and design algorithms for both estimation and control. The RL setting presents two particular challenges when CPT is applied: estimating the CPT objective requires estimations of the entire distribution of the value function and finding a randomized optimal policy. The estimation scheme that we propose uses the empirical distribution to estimate the CPT-value of a random variable. We then use this scheme in the inner loop of a CPT-value optimization procedure that is based on the well-known simulation optimization idea of simultaneous perturbation stochastic approximation (SPSA). We provide theoretical convergence guarantees for all the proposed algorithms and also illustrate the usefulness of CPT-based criteria in a traffic signal control application.

Adaptive system optimization using random directions stochastic approximation

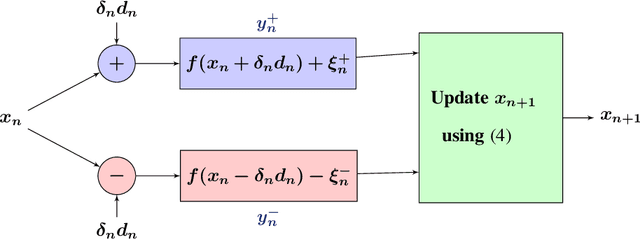
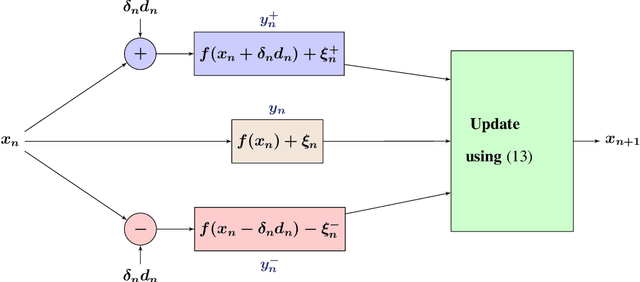
We present novel algorithms for simulation optimization using random directions stochastic approximation (RDSA). These include first-order (gradient) as well as second-order (Newton) schemes. We incorporate both continuous-valued as well as discrete-valued perturbations into both our algorithms. The former are chosen to be independent and identically distributed (i.i.d.) symmetric, uniformly distributed random variables (r.v.), while the latter are i.i.d., asymmetric, Bernoulli r.v.s. Our Newton algorithm, with a novel Hessian estimation scheme, requires N-dimensional perturbations and three loss measurements per iteration, whereas the simultaneous perturbation Newton search algorithm of [1] requires 2N-dimensional perturbations and four loss measurements per iteration. We prove the unbiasedness of both gradient and Hessian estimates and asymptotic (strong) convergence for both first-order and second-order schemes. We also provide asymptotic normality results, which in particular establish that the asymmetric Bernoulli variant of Newton RDSA method is better than 2SPSA of [1]. Numerical experiments are used to validate the theoretical results.