Adaptive system optimization using random directions stochastic approximation
Paper and Code
Aug 08, 2015
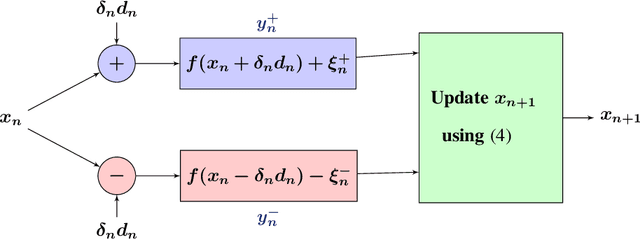
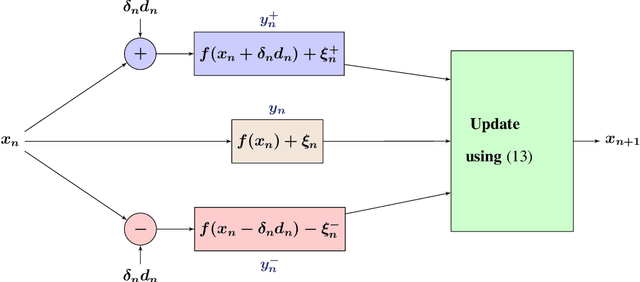

We present novel algorithms for simulation optimization using random directions stochastic approximation (RDSA). These include first-order (gradient) as well as second-order (Newton) schemes. We incorporate both continuous-valued as well as discrete-valued perturbations into both our algorithms. The former are chosen to be independent and identically distributed (i.i.d.) symmetric, uniformly distributed random variables (r.v.), while the latter are i.i.d., asymmetric, Bernoulli r.v.s. Our Newton algorithm, with a novel Hessian estimation scheme, requires N-dimensional perturbations and three loss measurements per iteration, whereas the simultaneous perturbation Newton search algorithm of [1] requires 2N-dimensional perturbations and four loss measurements per iteration. We prove the unbiasedness of both gradient and Hessian estimates and asymptotic (strong) convergence for both first-order and second-order schemes. We also provide asymptotic normality results, which in particular establish that the asymmetric Bernoulli variant of Newton RDSA method is better than 2SPSA of [1]. Numerical experiments are used to validate the theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge