High-Probability Bounds for SGD under the Polyak-Lojasiewicz Condition with Markovian Noise

We present the first uniform-in-time high-probability bound for SGD under the PL condition, where the gradient noise contains both Markovian and martingale difference components. This significantly broadens the scope of finite-time guarantees, as the PL condition arises in many machine learning and deep learning models while Markovian noise naturally arises in decentralized optimization and online system identification problems. We further allow the magnitude of noise to grow with the function value, enabling the analysis of many practical sampling strategies. In addition to the high-probability guarantee, we establish a matching $1/k$ decay rate for the expected suboptimality. Our proof technique relies on the Poisson equation to handle the Markovian noise and a probabilistic induction argument to address the lack of almost-sure bounds on the objective. Finally, we demonstrate the applicability of our framework by analyzing three practical optimization problems: token-based decentralized linear regression, supervised learning with subsampling for privacy amplification, and online system identification.

Generalized Random Direction Newton Algorithms for Stochastic Optimization

We present a family of generalized Hessian estimators of the objective using random direction stochastic approximation (RDSA) by utilizing only noisy function measurements. The form of each estimator and the order of the bias depend on the number of function measurements. In particular, we demonstrate that estimators with more function measurements exhibit lower-order estimation bias. We show the asymptotic unbiasedness of the estimators. We also perform asymptotic and non-asymptotic convergence analyses for stochastic Newton methods that incorporate our generalized Hessian estimators. Finally, we perform numerical experiments to validate our theoretical findings.

Convergence of Multiagent Learning Systems for Traffic control

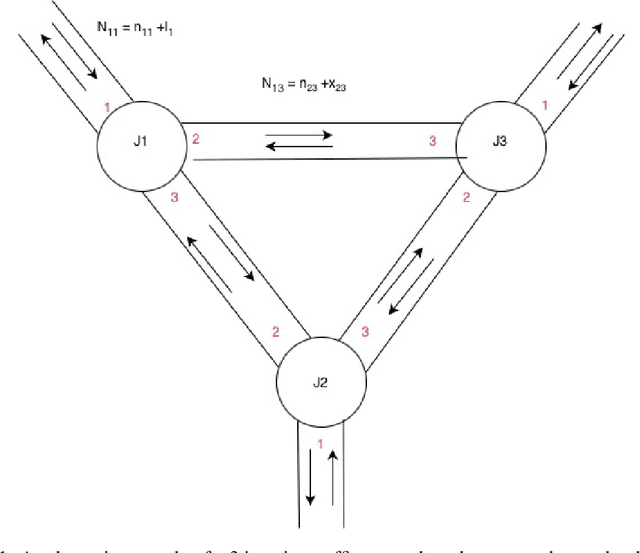
Rapid urbanization in cities like Bangalore has led to severe traffic congestion, making efficient Traffic Signal Control (TSC) essential. Multi-Agent Reinforcement Learning (MARL), often modeling each traffic signal as an independent agent using Q-learning, has emerged as a promising strategy to reduce average commuter delays. While prior work Prashant L A et. al has empirically demonstrated the effectiveness of this approach, a rigorous theoretical analysis of its stability and convergence properties in the context of traffic control has not been explored. This paper bridges that gap by focusing squarely on the theoretical basis of this multi-agent algorithm. We investigate the convergence problem inherent in using independent learners for the cooperative TSC task. Utilizing stochastic approximation methods, we formally analyze the learning dynamics. The primary contribution of this work is the proof that the specific multi-agent reinforcement learning algorithm for traffic control is proven to converge under the given conditions extending it from single agent convergence proofs for asynchronous value iteration.

Enabling Off-Policy Imitation Learning with Deep Actor Critic Stabilization

Learning complex policies with Reinforcement Learning (RL) is often hindered by instability and slow convergence, a problem exacerbated by the difficulty of reward engineering. Imitation Learning (IL) from expert demonstrations bypasses this reliance on rewards. However, state-of-the-art IL methods, exemplified by Generative Adversarial Imitation Learning (GAIL)Ho et. al, suffer from severe sample inefficiency. This is a direct consequence of their foundational on-policy algorithms, such as TRPO Schulman et.al. In this work, we introduce an adversarial imitation learning algorithm that incorporates off-policy learning to improve sample efficiency. By combining an off-policy framework with auxiliary techniques specifically, double Q network based stabilization and value learning without reward function inference we demonstrate a reduction in the samples required to robustly match expert behavior.

An Actor-Critic Algorithm with Function Approximation for Risk Sensitive Cost Markov Decision Processes

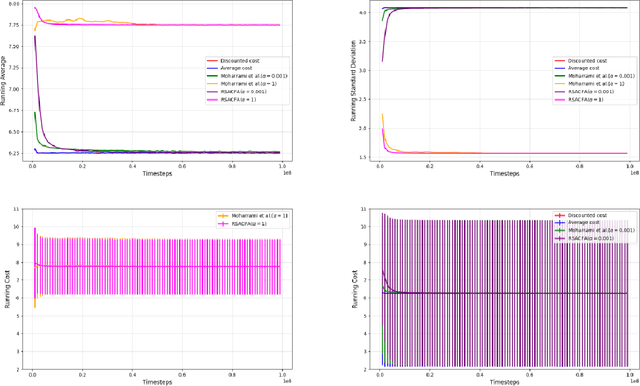
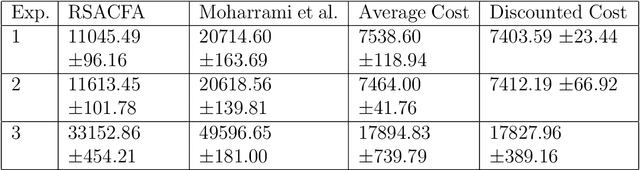
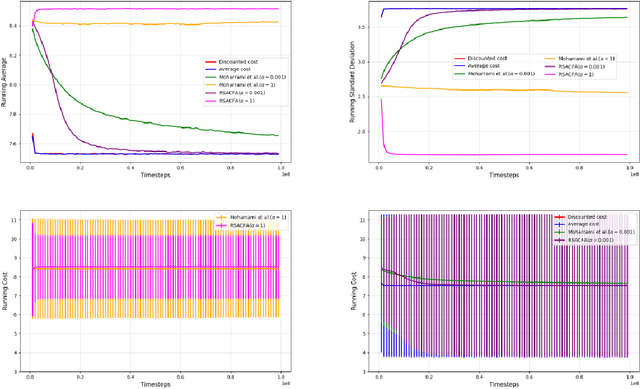
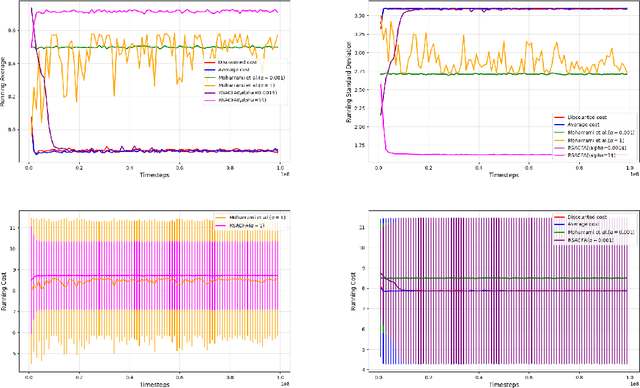
In this paper, we consider the risk-sensitive cost criterion with exponentiated costs for Markov decision processes and develop a model-free policy gradient algorithm in this setting. Unlike additive cost criteria such as average or discounted cost, the risk-sensitive cost criterion is less studied due to the complexity resulting from the multiplicative structure of the resulting Bellman equation. We develop an actor-critic algorithm with function approximation in this setting and provide its asymptotic convergence analysis. We also show the results of numerical experiments that demonstrate the superiority in performance of our algorithm over other recent algorithms in the literature.

Gradient-Weighted Feature Back-Projection: A Fast Alternative to Feature Distillation in 3D Gaussian Splatting

We introduce a training-free method for feature field rendering in Gaussian splatting. Our approach back-projects 2D features into pre-trained 3D Gaussians, using a weighted sum based on each Gaussian's influence in the final rendering. While most training-based feature field rendering methods excel at 2D segmentation but perform poorly at 3D segmentation without post-processing, our method achieves high-quality results in both 2D and 3D segmentation. Experimental results demonstrate that our approach is fast, scalable, and offers performance comparable to training-based methods.

Gradient-Driven 3D Segmentation and Affordance Transfer in Gaussian Splatting Using 2D Masks

3D Gaussian Splatting has emerged as a powerful 3D scene representation technique, capturing fine details with high efficiency. In this paper, we introduce a novel voting-based method that extends 2D segmentation models to 3D Gaussian splats. Our approach leverages masked gradients, where gradients are filtered by input 2D masks, and these gradients are used as votes to achieve accurate segmentation. As a byproduct, we discovered that inference-time gradients can also be used to prune Gaussians, resulting in up to 21% compression. Additionally, we explore few-shot affordance transfer, allowing annotations from 2D images to be effectively transferred onto 3D Gaussian splats. The robust yet straightforward mathematical formulation underlying this approach makes it a highly effective tool for numerous downstream applications, such as augmented reality (AR), object editing, and robotics. The project code and additional resources are available at https://jojijoseph.github.io/3dgs-segmentation.

Critic-Actor for Average Reward MDPs with Function Approximation: A Finite-Time Analysis

In recent years, there has been a lot of research work activity focused on carrying out asymptotic and non-asymptotic convergence analyses for two-timescale actor critic algorithms where the actor updates are performed on a timescale that is slower than that of the critic. In a recent work, the critic-actor algorithm has been presented for the infinite horizon discounted cost setting in the look-up table case where the timescales of the actor and the critic are reversed and asymptotic convergence analysis has been presented. In our work, we present the first critic-actor algorithm with function approximation and in the long-run average reward setting and present the first finite-time (non-asymptotic) analysis of such a scheme. We obtain optimal learning rates and prove that our algorithm achieves a sample complexity of $\mathcal{\tilde{O}}(\epsilon^{-2.08})$ for the mean squared error of the critic to be upper bounded by $\epsilon$ which is better than the one obtained for actor-critic in a similar setting. We also show the results of numerical experiments on three benchmark settings and observe that the critic-actor algorithm competes well with the actor-critic algorithm.

Approximate Linear Programming and Decentralized Policy Improvement in Cooperative Multi-agent Markov Decision Processes

In this work, we consider a `cooperative' multi-agent Markov decision process (MDP) involving m greater than 1 agents, where all agents are aware of the system model. At each decision epoch, all the m agents cooperatively select actions in order to maximize a common long-term objective. Since the number of actions grows exponentially in the number of agents, policy improvement is computationally expensive. Recent works have proposed using decentralized policy improvement in which each agent assumes that the decisions of the other agents are fixed and it improves its decisions unilaterally. Yet, in these works, exact values are computed. In our work, for cooperative multi-agent finite and infinite horizon discounted MDPs, we propose suitable approximate policy iteration algorithms, wherein we use approximate linear programming to compute the approximate value function and use decentralized policy improvement. Thus our algorithms can handle both large number of states as well as multiple agents. We provide theoretical guarantees for our algorithms and also demonstrate the performance of our algorithms on some numerical examples.

Finite Time Analysis of Constrained Actor Critic and Constrained Natural Actor Critic Algorithms

Actor Critic methods have found immense applications on a wide range of Reinforcement Learning tasks especially when the state-action space is large. In this paper, we consider actor critic and natural actor critic algorithms with function approximation for constrained Markov decision processes (C-MDP) involving inequality constraints and carry out a non-asymptotic analysis for both of these algorithms in a non-i.i.d (Markovian) setting. We consider the long-run average cost criterion where both the objective and the constraint functions are suitable policy-dependent long-run averages of certain prescribed cost functions. We handle the inequality constraints using the Lagrange multiplier method. We prove that these algorithms are guaranteed to find a first-order stationary point (i.e., $\Vert \nabla L(\theta,\gamma)\Vert_2^2 \leq \epsilon$) of the performance (Lagrange) function $L(\theta,\gamma)$, with a sample complexity of $\mathcal{\tilde{O}}(\epsilon^{-2.5})$ in the case of both Constrained Actor Critic (C-AC) and Constrained Natural Actor Critic (C-NAC) algorithms.We also show the results of experiments on a few different grid world settings and observe good empirical performance using both of these algorithms. In particular, for large grid sizes, Constrained Natural Actor Critic shows slightly better results than Constrained Actor Critic while the latter is slightly better for a small grid size.