A Cubic-regularized Policy Newton Algorithm for Reinforcement Learning

We consider the problem of control in the setting of reinforcement learning (RL), where model information is not available. Policy gradient algorithms are a popular solution approach for this problem and are usually shown to converge to a stationary point of the value function. In this paper, we propose two policy Newton algorithms that incorporate cubic regularization. Both algorithms employ the likelihood ratio method to form estimates of the gradient and Hessian of the value function using sample trajectories. The first algorithm requires an exact solution of the cubic regularized problem in each iteration, while the second algorithm employs an efficient gradient descent-based approximation to the cubic regularized problem. We establish convergence of our proposed algorithms to a second-order stationary point (SOSP) of the value function, which results in the avoidance of traps in the form of saddle points. In particular, the sample complexity of our algorithms to find an $\epsilon$-SOSP is $O(\epsilon^{-3.5})$, which is an improvement over the state-of-the-art sample complexity of $O(\epsilon^{-4.5})$.

A Gradient Smoothed Functional Algorithm with Truncated Cauchy Random Perturbations for Stochastic Optimization

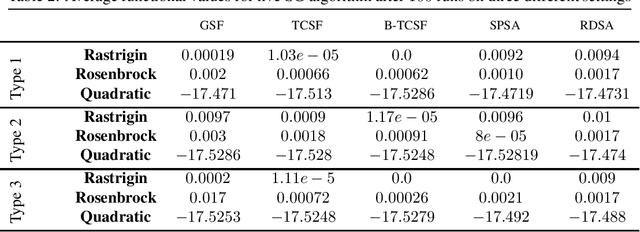
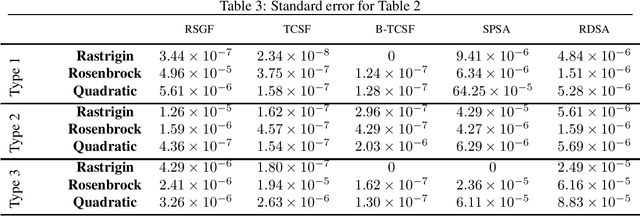
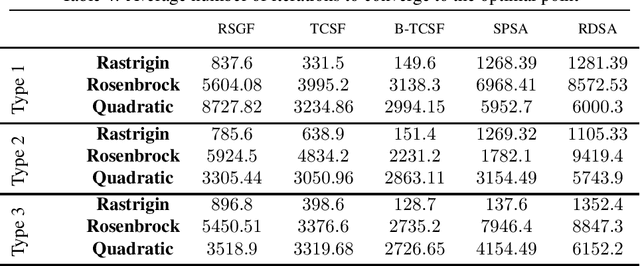
In this paper, we present a stochastic gradient algorithm for minimizing a smooth objective function that is an expectation over noisy cost samples and only the latter are observed for any given parameter. Our algorithm employs a gradient estimation scheme with random perturbations, which are formed using the truncated Cauchy distribution from the unit sphere. We analyze the bias and variance of the proposed gradient estimator. Our algorithm is found to be particularly useful in the case when the objective function is non-convex, and the parameter dimension is high. From an asymptotic convergence analysis, we establish that our algorithm converges almost surely to the set of stationary points of the objective function and obtain the asymptotic convergence rate. We also show that our algorithm avoids unstable equilibria, implying convergence to local minima. Further, we perform a non-asymptotic convergence analysis of our algorithm. In particular, we establish here a non-asymptotic bound for finding an $\epsilon$-stationary point of the non-convex objective function. Finally, we demonstrate numerically through simulations that the performance of our algorithm outperforms GSF, SPSA and RDSA by a significant margin over a few non-convex settings and further validate its performance over convex (noisy) objectives.

WASSUP? LOL : Characterizing Out-of-Vocabulary Words in Twitter

Language in social media is mostly driven by new words and spellings that are constantly entering the lexicon thereby polluting it and resulting in high deviation from the formal written version. The primary entities of such language are the out-of-vocabulary (OOV) words. In this paper, we study various sociolinguistic properties of the OOV words and propose a classification model to categorize them into at least six categories. We achieve 81.26% accuracy with high precision and recall. We observe that the content features are the most discriminative ones followed by lexical and context features.