A Gradient Smoothed Functional Algorithm with Truncated Cauchy Random Perturbations for Stochastic Optimization

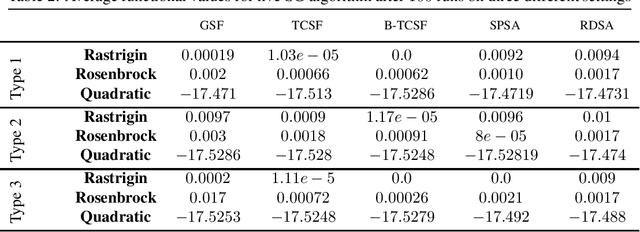
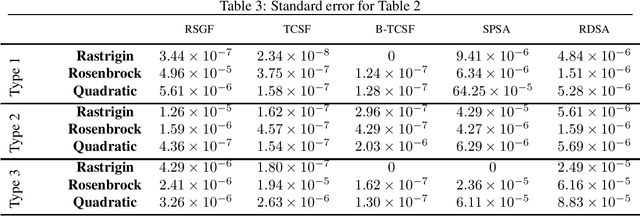
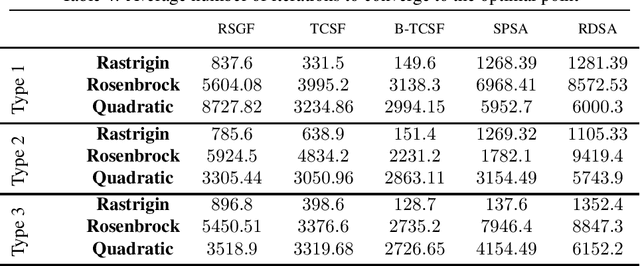
In this paper, we present a stochastic gradient algorithm for minimizing a smooth objective function that is an expectation over noisy cost samples and only the latter are observed for any given parameter. Our algorithm employs a gradient estimation scheme with random perturbations, which are formed using the truncated Cauchy distribution from the unit sphere. We analyze the bias and variance of the proposed gradient estimator. Our algorithm is found to be particularly useful in the case when the objective function is non-convex, and the parameter dimension is high. From an asymptotic convergence analysis, we establish that our algorithm converges almost surely to the set of stationary points of the objective function and obtain the asymptotic convergence rate. We also show that our algorithm avoids unstable equilibria, implying convergence to local minima. Further, we perform a non-asymptotic convergence analysis of our algorithm. In particular, we establish here a non-asymptotic bound for finding an $\epsilon$-stationary point of the non-convex objective function. Finally, we demonstrate numerically through simulations that the performance of our algorithm outperforms GSF, SPSA and RDSA by a significant margin over a few non-convex settings and further validate its performance over convex (noisy) objectives.