Soumyajit Guin
An Actor-Critic Algorithm with Function Approximation for Risk Sensitive Cost Markov Decision Processes
Feb 17, 2025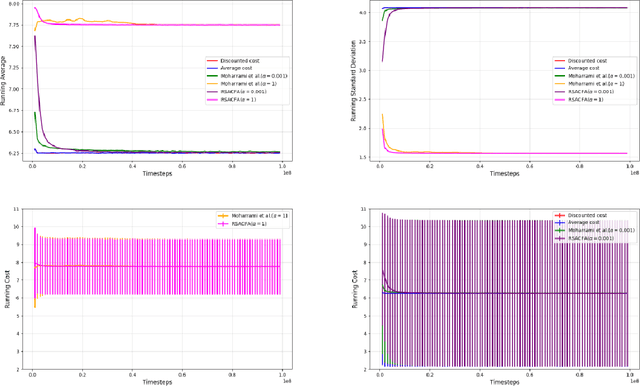
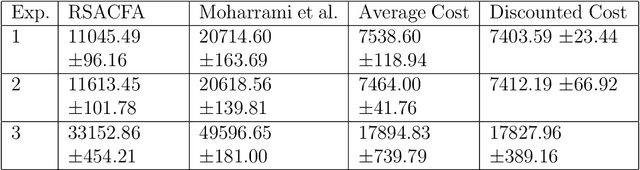
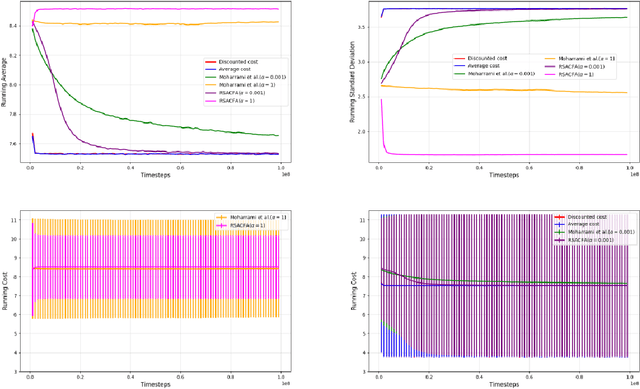
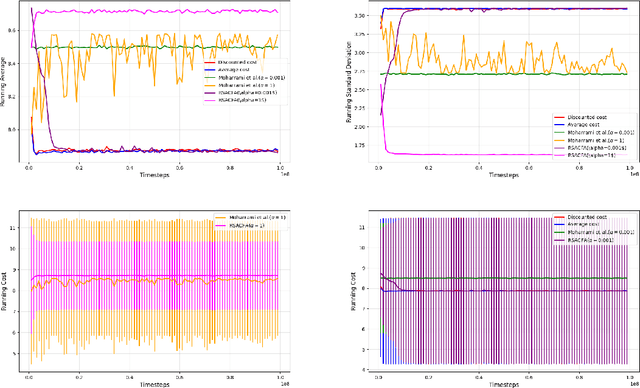
Abstract:In this paper, we consider the risk-sensitive cost criterion with exponentiated costs for Markov decision processes and develop a model-free policy gradient algorithm in this setting. Unlike additive cost criteria such as average or discounted cost, the risk-sensitive cost criterion is less studied due to the complexity resulting from the multiplicative structure of the resulting Bellman equation. We develop an actor-critic algorithm with function approximation in this setting and provide its asymptotic convergence analysis. We also show the results of numerical experiments that demonstrate the superiority in performance of our algorithm over other recent algorithms in the literature.
A policy gradient approach for Finite Horizon Constrained Markov Decision Processes
Oct 10, 2022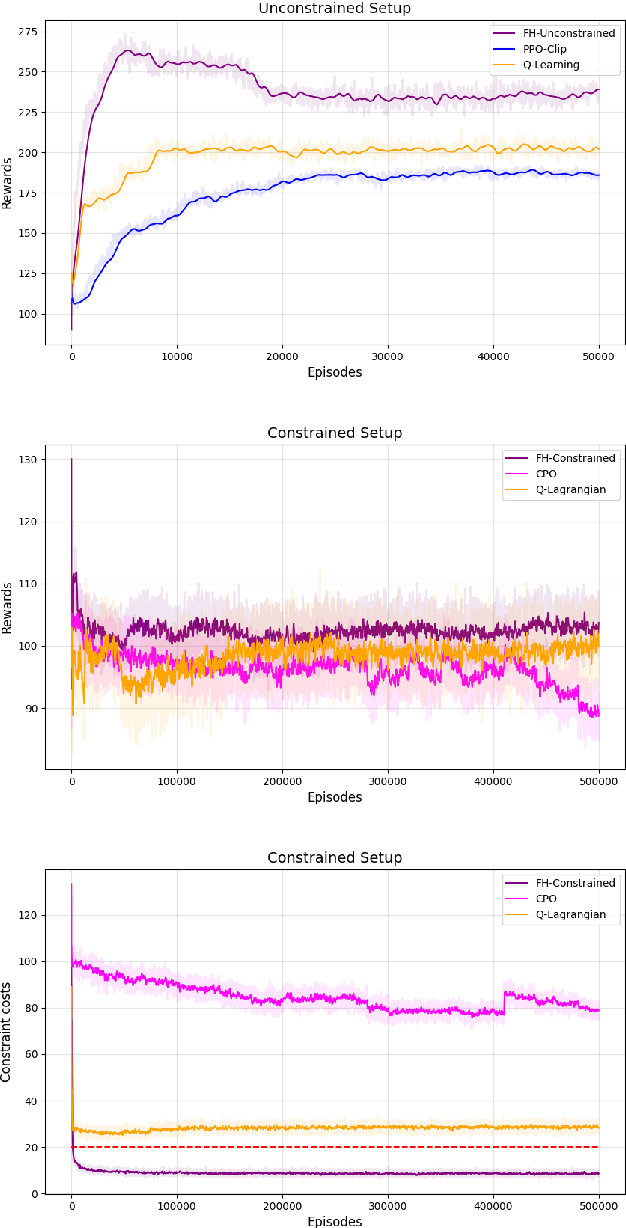
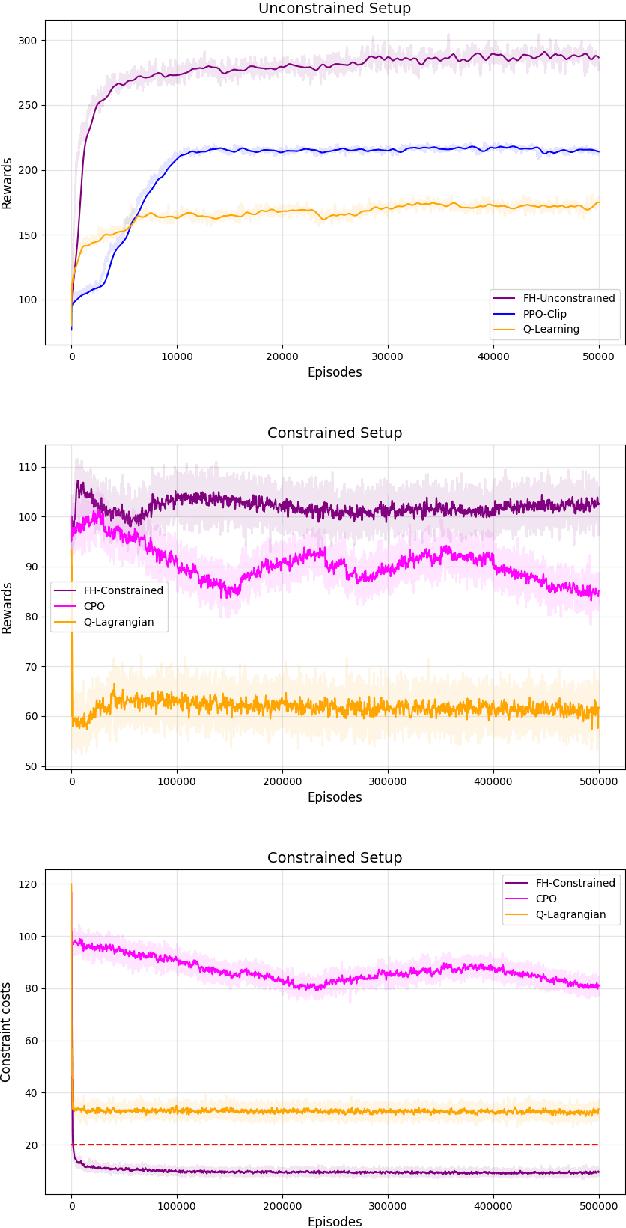
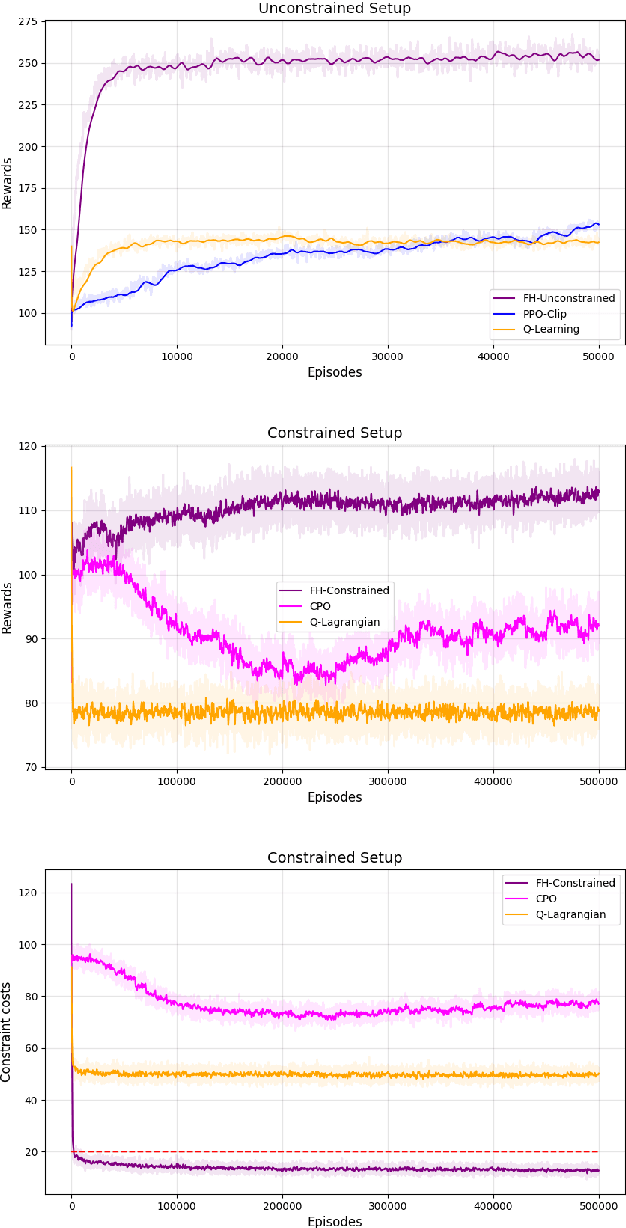
Abstract:The infinite horizon setting is widely adopted for problems of reinforcement learning (RL). These invariably result in stationary policies that are optimal. In many situations, finite horizon control problems are of interest and for such problems, the optimal policies are time-varying in general. Another setting that has become popular in recent times is of Constrained Reinforcement Learning, where the agent maximizes its rewards while also aims to satisfy certain constraint criteria. However, this setting has only been studied in the context of infinite horizon MDPs where stationary policies are optimal. We present, for the first time, an algorithm for constrained RL in the Finite Horizon Setting where the horizon terminates after a fixed (finite) time. We use function approximation in our algorithm which is essential when the state and action spaces are large or continuous and use the policy gradient method to find the optimal policy. The optimal policy that we obtain depends on the stage and so is time-dependent. To the best of our knowledge, our paper presents the first policy gradient algorithm for the finite horizon setting with constraints. We show the convergence of our algorithm to an optimal policy. We further present a sample complexity result for our algorithm in the unconstrained (i.e., the regular finite horizon MDP) setting. We also compare and analyze the performance of our algorithm through experiments and show that our algorithm performs better than other well known algorithms.
Actor-Critic or Critic-Actor? A Tale of Two Time Scales
Oct 10, 2022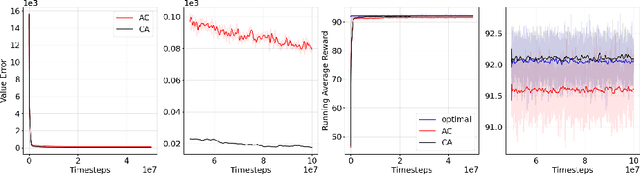
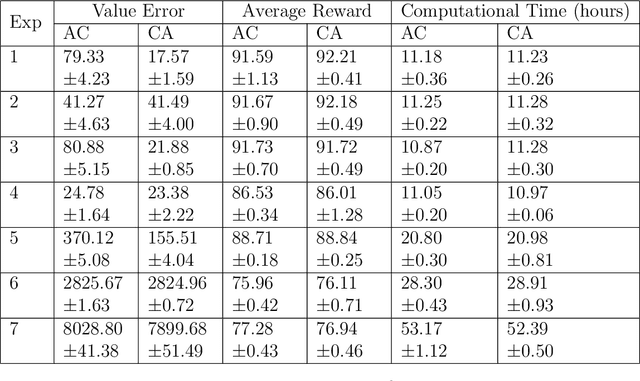
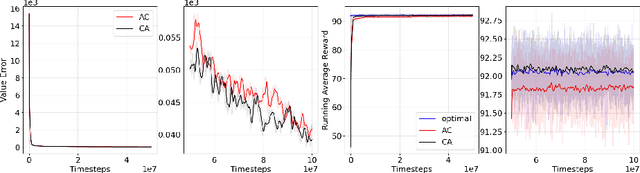
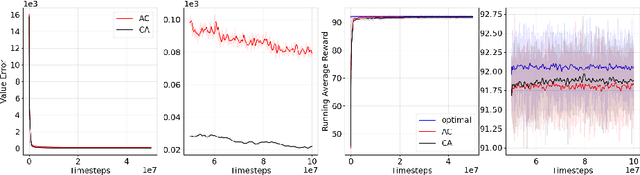
Abstract:We revisit the standard formulation of tabular actor-critic algorithm as a two time-scale stochastic approximation with value function computed on a faster time-scale and policy computed on a slower time-scale. This emulates policy iteration. We begin by observing that reversal of the time scales will in fact emulate value iteration and is a legitimate algorithm. We compare the two empirically with and without function approximation (with both linear and nonlinear function approximators) and observe that our proposed critic-actor algorithm performs better empirically though with a marginal increase in the computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge