Vivek S. Borkar
An Actor-Critic Algorithm with Function Approximation for Risk Sensitive Cost Markov Decision Processes
Feb 17, 2025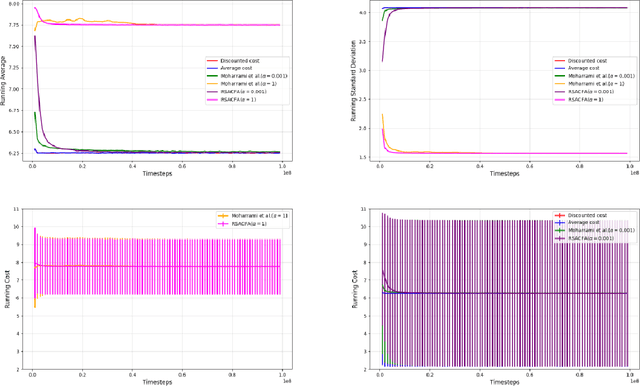
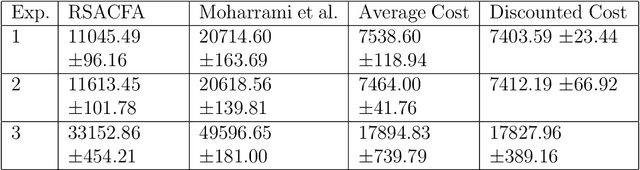
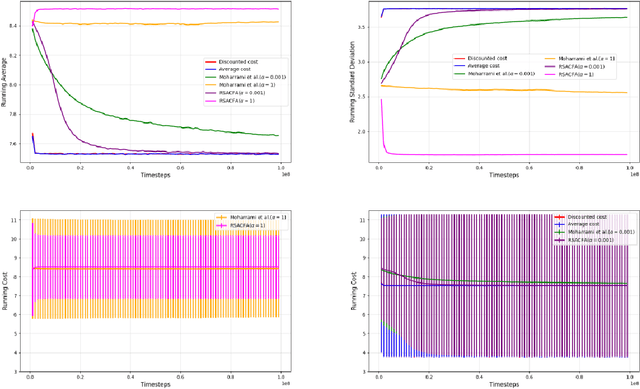
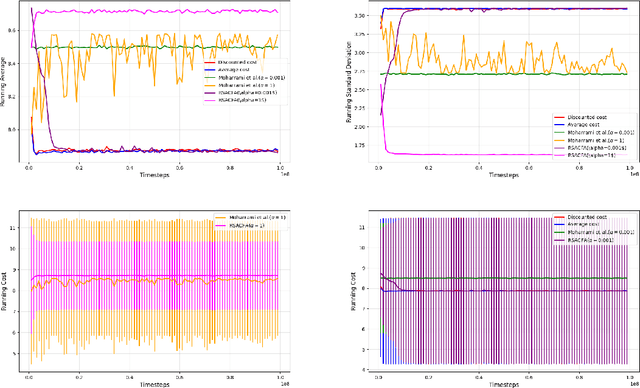
Abstract:In this paper, we consider the risk-sensitive cost criterion with exponentiated costs for Markov decision processes and develop a model-free policy gradient algorithm in this setting. Unlike additive cost criteria such as average or discounted cost, the risk-sensitive cost criterion is less studied due to the complexity resulting from the multiplicative structure of the resulting Bellman equation. We develop an actor-critic algorithm with function approximation in this setting and provide its asymptotic convergence analysis. We also show the results of numerical experiments that demonstrate the superiority in performance of our algorithm over other recent algorithms in the literature.
Lagrangian Index Policy for Restless Bandits with Average Reward
Dec 17, 2024



Abstract:We study the Lagrangian Index Policy (LIP) for restless multi-armed bandits with long-run average reward. In particular, we compare the performance of LIP with the performance of the Whittle Index Policy (WIP), both heuristic policies known to be asymptotically optimal under certain natural conditions. Even though in most cases their performances are very similar, in the cases when WIP shows bad performance, LIP continues to perform very well. We then propose reinforcement learning algorithms, both tabular and NN-based, to obtain online learning schemes for LIP in the model-free setting. The proposed reinforcement learning schemes for LIP requires significantly less memory than the analogous scheme for WIP. We calculate analytically the Lagrangian index for the restart model, which describes the optimal web crawling and the minimization of the weighted age of information. We also give a new proof of asymptotic optimality in case of homogeneous bandits as the number of arms goes to infinity, based on exchangeability and de Finetti's theorem.
A Concentration Bound for TD with Function Approximation
Dec 16, 2023Abstract:We derive a concentration bound of the type `for all $n \geq n_0$ for some $n_0$' for TD(0) with linear function approximation. We work with online TD learning with samples from a single sample path of the underlying Markov chain. This makes our analysis significantly different from offline TD learning or TD learning with access to independent samples from the stationary distribution of the Markov chain. We treat TD(0) as a contractive stochastic approximation algorithm, with both martingale and Markov noises. Markov noise is handled using the Poisson equation and the lack of almost sure guarantees on boundedness of iterates is handled using the concept of relaxed concentration inequalities.
Approximation of Convex Envelope Using Reinforcement Learning
Nov 24, 2023



Abstract:Oberman gave a stochastic control formulation of the problem of estimating the convex envelope of a non-convex function. Based on this, we develop a reinforcement learning scheme to approximate the convex envelope, using a variant of Q-learning for controlled optimal stopping. It shows very promising results on a standard library of test problems.
Decentralised Q-Learning for Multi-Agent Markov Decision Processes with a Satisfiability Criterion
Nov 21, 2023Abstract:In this paper, we propose a reinforcement learning algorithm to solve a multi-agent Markov decision process (MMDP). The goal, inspired by Blackwell's Approachability Theorem, is to lower the time average cost of each agent to below a pre-specified agent-specific bound. For the MMDP, we assume the state dynamics to be controlled by the joint actions of agents, but the per-stage costs to only depend on the individual agent's actions. We combine the Q-learning algorithm for a weighted combination of the costs of each agent, obtained by a gossip algorithm with the Metropolis-Hastings or Multiplicative Weights formalisms to modulate the averaging matrix of the gossip. We use multiple timescales in our algorithm and prove that under mild conditions, it approximately achieves the desired bounds for each of the agents. We also demonstrate the empirical performance of this algorithm in the more general setting of MMDPs having jointly controlled per-stage costs.
Actor-Critic or Critic-Actor? A Tale of Two Time Scales
Oct 10, 2022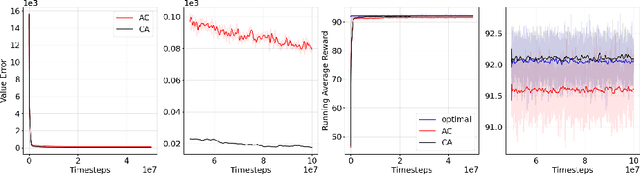
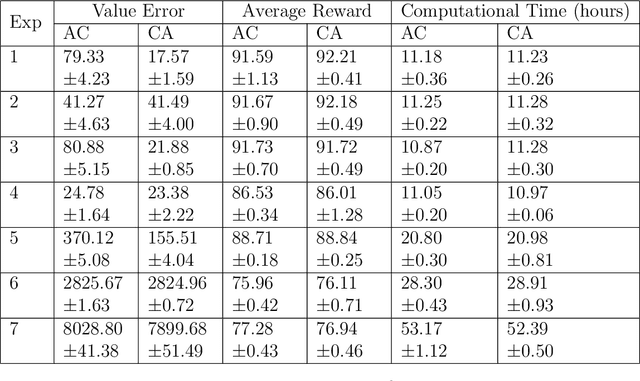
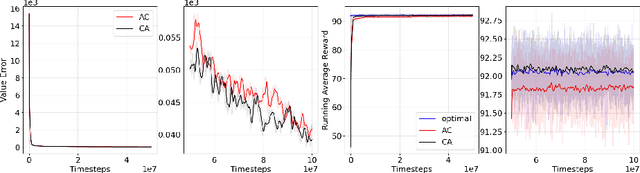
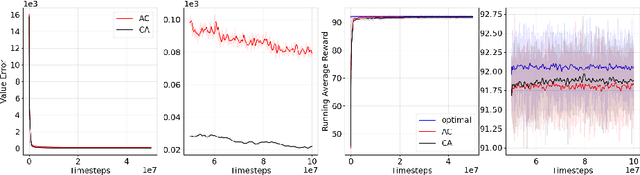
Abstract:We revisit the standard formulation of tabular actor-critic algorithm as a two time-scale stochastic approximation with value function computed on a faster time-scale and policy computed on a slower time-scale. This emulates policy iteration. We begin by observing that reversal of the time scales will in fact emulate value iteration and is a legitimate algorithm. We compare the two empirically with and without function approximation (with both linear and nonlinear function approximators) and observe that our proposed critic-actor algorithm performs better empirically though with a marginal increase in the computational cost.
A Concentration Bound for LSPE($λ$)
Nov 04, 2021Abstract:The popular LSPE($\lambda$) algorithm for policy evaluation is revisited to derive a concentration bound that gives high probability performance guarantees from some time on.
Concentration of Contractive Stochastic Approximation and Reinforcement Learning
Jun 27, 2021Abstract:Using a martingale concentration inequality, concentration bounds `from time $n_0$ on' are derived for stochastic approximation algorithms with contractive maps and both martingale difference and Markov noises. These are applied to reinforcement learning algorithms, in particular to asynchronous Q-learning and TD(0).
Dynamic social learning under graph constraints
Jul 08, 2020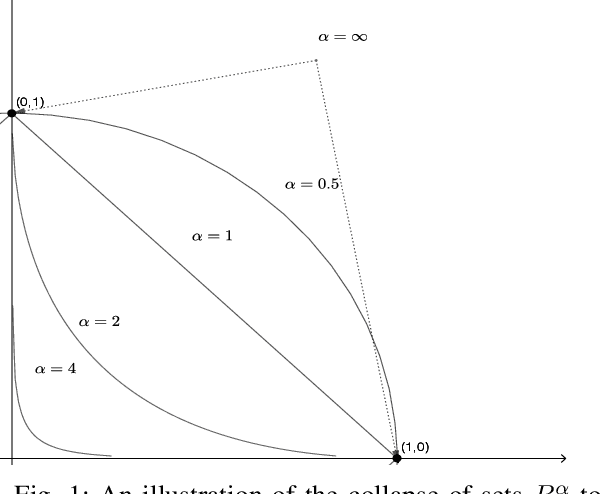
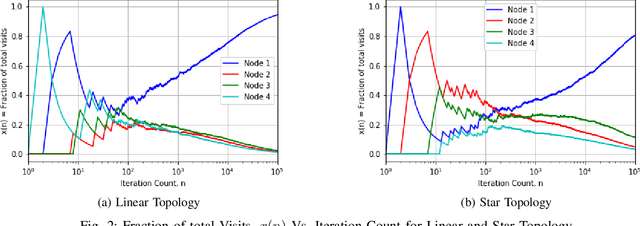
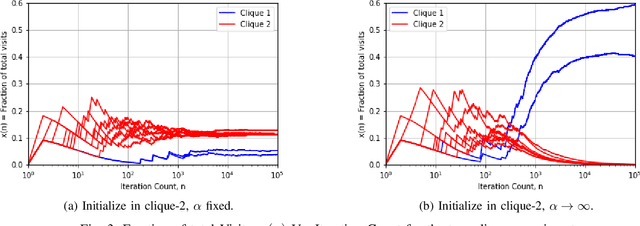
Abstract:We argue that graph-constrained dynamic choice with reinforcement can be viewed as a scaled version of a special instance of replicator dynamics. The latter also arises as the limiting differential equation for the empirical measures of a vertex reinforced random walk on a directed graph. We use this equivalence to show that for a class of positively $\alpha$-homogeneous rewards, $\alpha > 0$, the asymptotic outcome concentrates around the optimum in a certain limiting sense when `annealed' by letting $\alpha\uparrow\infty$ slowly. We also discuss connections with classical simulated annealing.
Whittle index based Q-learning for restless bandits with average reward
Apr 29, 2020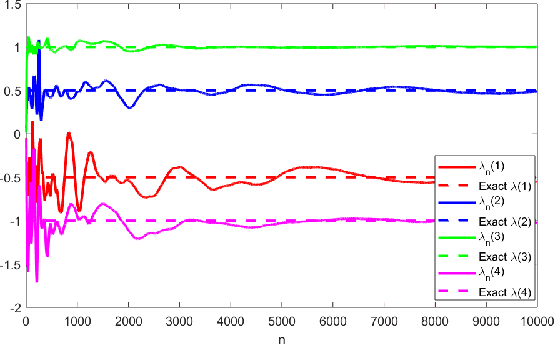
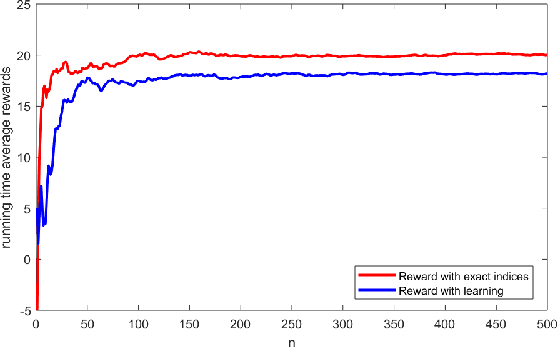
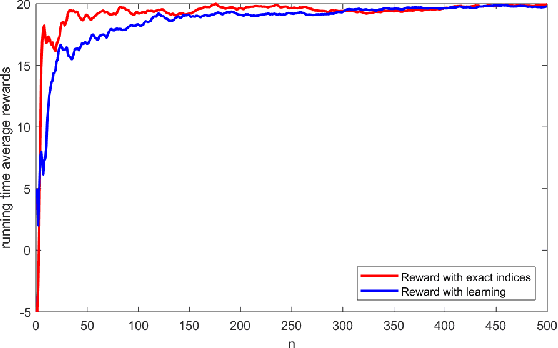
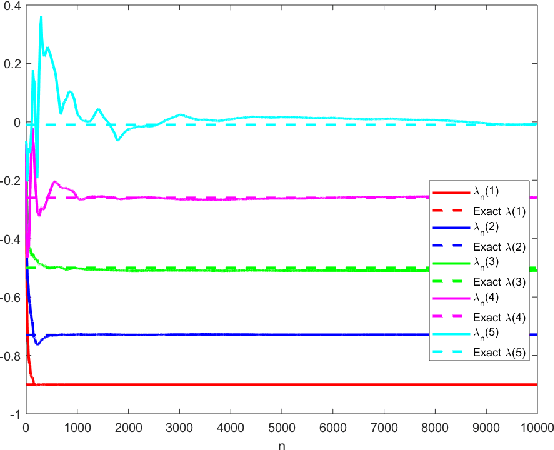
Abstract:A novel reinforcement learning algorithm is introduced for multiarmed restless bandits with average reward, using the paradigms of Q-learning and Whittle index. Specifically, we leverage the structure of the Whittle index policy to reduce the search space of Q-learning, resulting in major computational gains. Rigorous convergence analysis is provided, supported by numerical experiments. The numerical experiments show excellent empirical performance of the proposed scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge