Adaptive Consensus: A network pruning approach for decentralized optimization

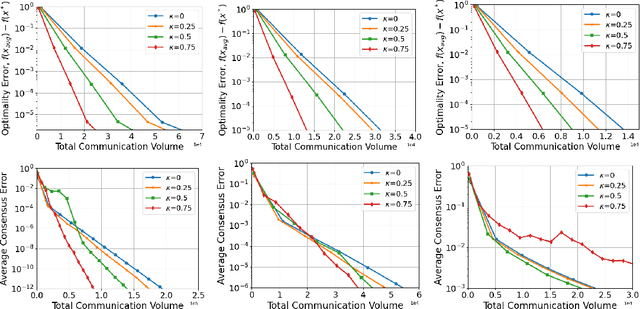
We consider network-based decentralized optimization problems, where each node in the network possesses a local function and the objective is to collectively attain a consensus solution that minimizes the sum of all the local functions. A major challenge in decentralized optimization is the reliance on communication which remains a considerable bottleneck in many applications. To address this challenge, we propose an adaptive randomized communication-efficient algorithmic framework that reduces the volume of communication by periodically tracking the disagreement error and judiciously selecting the most influential and effective edges at each node for communication. Within this framework, we present two algorithms: Adaptive Consensus (AC) to solve the consensus problem and Adaptive Consensus based Gradient Tracking (AC-GT) to solve smooth strongly convex decentralized optimization problems. We establish strong theoretical convergence guarantees for the proposed algorithms and quantify their performance in terms of various algorithmic parameters under standard assumptions. Finally, numerical experiments showcase the effectiveness of the framework in significantly reducing the information exchange required to achieve a consensus solution.

Dynamic social learning under graph constraints

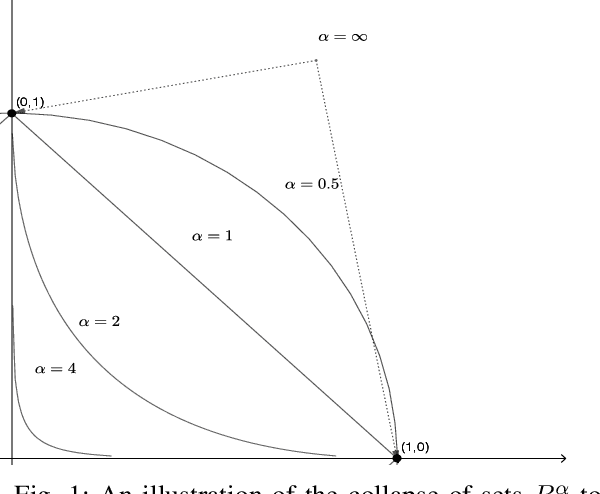
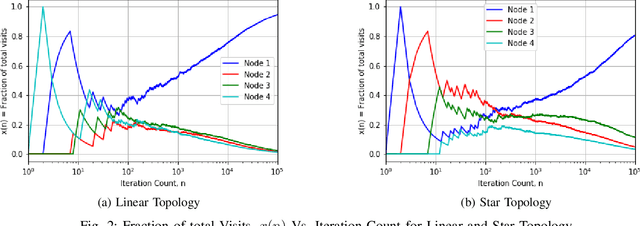
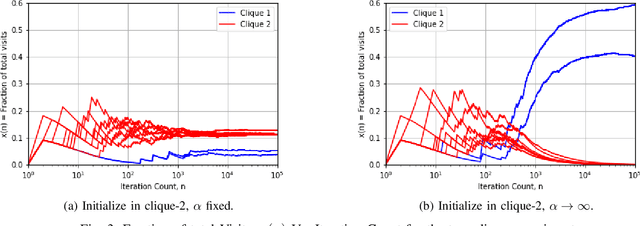
We argue that graph-constrained dynamic choice with reinforcement can be viewed as a scaled version of a special instance of replicator dynamics. The latter also arises as the limiting differential equation for the empirical measures of a vertex reinforced random walk on a directed graph. We use this equivalence to show that for a class of positively $\alpha$-homogeneous rewards, $\alpha > 0$, the asymptotic outcome concentrates around the optimum in a certain limiting sense when `annealed' by letting $\alpha\uparrow\infty$ slowly. We also discuss connections with classical simulated annealing.