Fast Unconstrained Optimization via Hessian Averaging and Adaptive Gradient Sampling Methods

We consider minimizing finite-sum and expectation objective functions via Hessian-averaging based subsampled Newton methods. These methods allow for gradient inexactness and have fixed per-iteration Hessian approximation costs. The recent work (Na et al. 2023) demonstrated that Hessian averaging can be utilized to achieve fast $\mathcal{O}\left(\sqrt{\tfrac{\log k}{k}}\right)$ local superlinear convergence for strongly convex functions in high probability, while maintaining fixed per-iteration Hessian costs. These methods, however, require gradient exactness and strong convexity, which poses challenges for their practical implementation. To address this concern we consider Hessian-averaged methods that allow gradient inexactness via norm condition based adaptive-sampling strategies. For the finite-sum problem we utilize deterministic sampling techniques which lead to global linear and sublinear convergence rates for strongly convex and nonconvex functions respectively. In this setting we are able to derive an improved deterministic local superlinear convergence rate of $\mathcal{O}\left(\tfrac{1}{k}\right)$. For the %expected risk expectation problem we utilize stochastic sampling techniques, and derive global linear and sublinear rates for strongly convex and nonconvex functions, as well as a $\mathcal{O}\left(\tfrac{1}{\sqrt{k}}\right)$ local superlinear convergence rate, all in expectation. We present novel analysis techniques that differ from the previous probabilistic results. Additionally, we propose scalable and efficient variations of these methods via diagonal approximations and derive the novel diagonally-averaged Newton (Dan) method for large-scale problems. Our numerical results demonstrate that the Hessian averaging not only helps with convergence, but can lead to state-of-the-art performance on difficult problems such as CIFAR100 classification with ResNets.

Adaptive Consensus: A network pruning approach for decentralized optimization

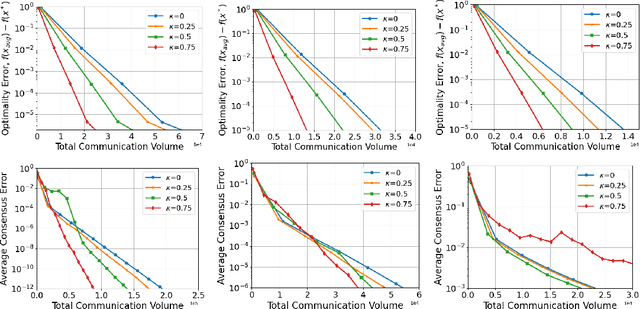
We consider network-based decentralized optimization problems, where each node in the network possesses a local function and the objective is to collectively attain a consensus solution that minimizes the sum of all the local functions. A major challenge in decentralized optimization is the reliance on communication which remains a considerable bottleneck in many applications. To address this challenge, we propose an adaptive randomized communication-efficient algorithmic framework that reduces the volume of communication by periodically tracking the disagreement error and judiciously selecting the most influential and effective edges at each node for communication. Within this framework, we present two algorithms: Adaptive Consensus (AC) to solve the consensus problem and Adaptive Consensus based Gradient Tracking (AC-GT) to solve smooth strongly convex decentralized optimization problems. We establish strong theoretical convergence guarantees for the proposed algorithms and quantify their performance in terms of various algorithmic parameters under standard assumptions. Finally, numerical experiments showcase the effectiveness of the framework in significantly reducing the information exchange required to achieve a consensus solution.

On the fast convergence of minibatch heavy ball momentum

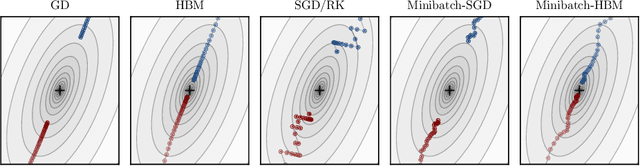
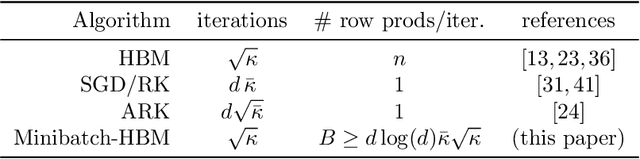
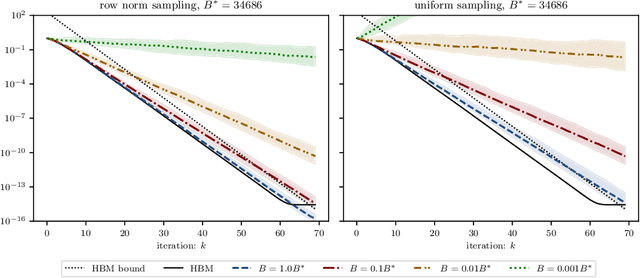
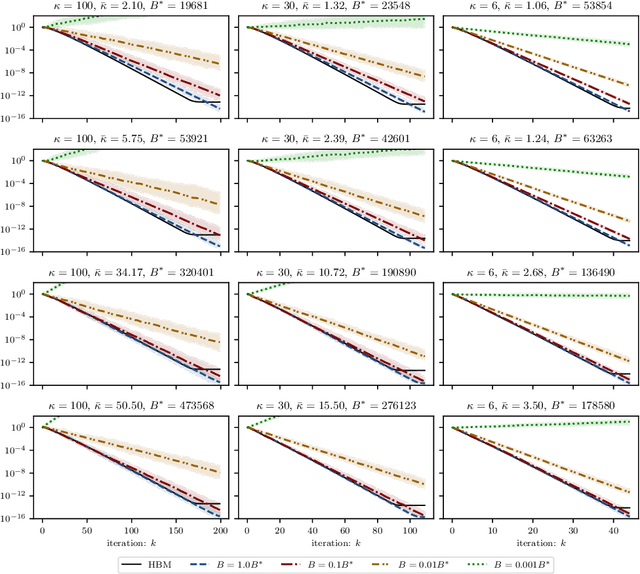
Simple stochastic momentum methods are widely used in machine learning optimization, but their good practical performance is at odds with an absence of theoretical guarantees of acceleration in the literature. In this work, we aim to close the gap between theory and practice by showing that stochastic heavy ball momentum, which can be interpreted as a randomized Kaczmarz algorithm with momentum, retains the fast linear rate of (deterministic) heavy ball momentum on quadratic optimization problems, at least when minibatching with a sufficiently large batch size is used. The analysis relies on carefully decomposing the momentum transition matrix, and using new spectral norm concentration bounds for products of independent random matrices. We provide numerical experiments to demonstrate that our bounds are reasonably sharp.

Adaptive Sampling Quasi-Newton Methods for Zeroth-Order Stochastic Optimization

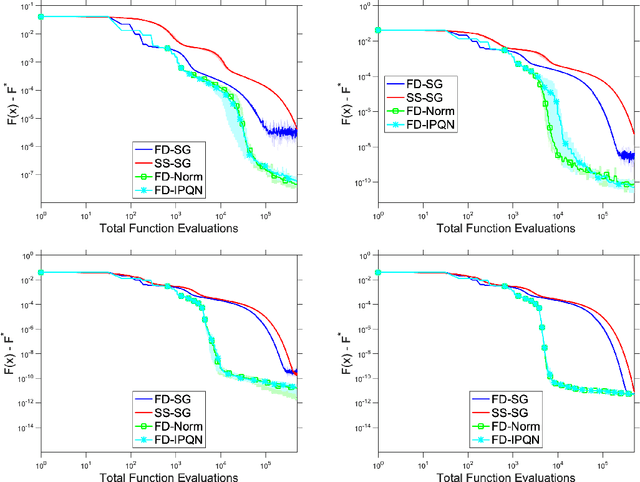
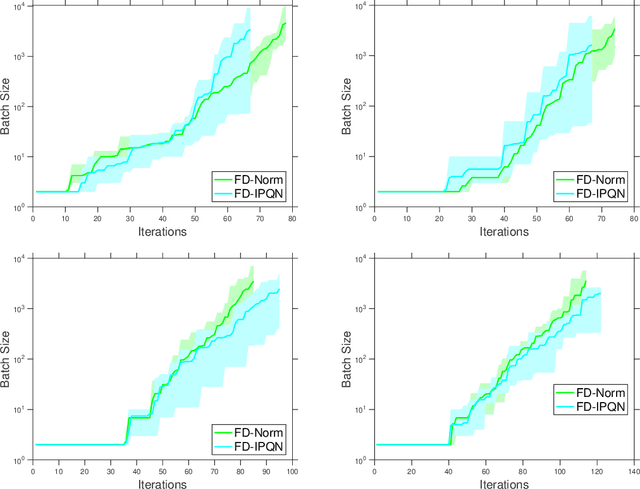
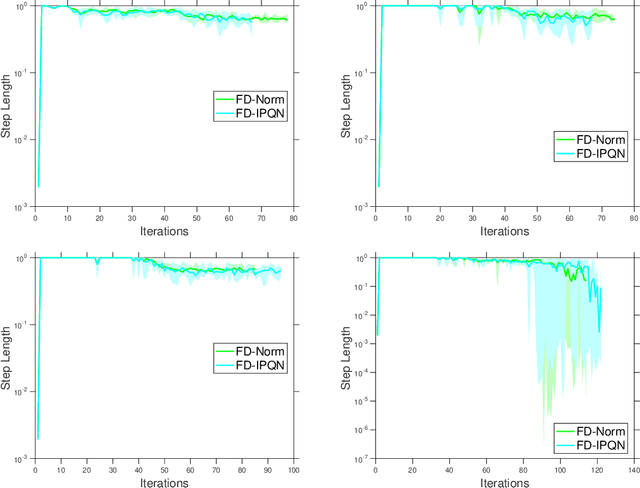
We consider unconstrained stochastic optimization problems with no available gradient information. Such problems arise in settings from derivative-free simulation optimization to reinforcement learning. We propose an adaptive sampling quasi-Newton method where we estimate the gradients of a stochastic function using finite differences within a common random number framework. We develop modified versions of a norm test and an inner product quasi-Newton test to control the sample sizes used in the stochastic approximations and provide global convergence results to the neighborhood of the optimal solution. We present numerical experiments on simulation optimization problems to illustrate the performance of the proposed algorithm. When compared with classical zeroth-order stochastic gradient methods, we observe that our strategies of adapting the sample sizes significantly improve performance in terms of the number of stochastic function evaluations required.

Retrospective Approximation for Smooth Stochastic Optimization

We consider stochastic optimization problems where a smooth (and potentially nonconvex) objective is to be minimized using a stochastic first-order oracle. These type of problems arise in many settings from simulation optimization to deep learning. We present Retrospective Approximation (RA) as a universal sequential sample-average approximation (SAA) paradigm where during each iteration $k$, a sample-path approximation problem is implicitly generated using an adapted sample size $M_k$, and solved (with prior solutions as "warm start") to an adapted error tolerance $\epsilon_k$, using a "deterministic method" such as the line search quasi-Newton method. The principal advantage of RA is that decouples optimization from stochastic approximation, allowing the direct adoption of existing deterministic algorithms without modification, thus mitigating the need to redesign algorithms for the stochastic context. A second advantage is the obvious manner in which RA lends itself to parallelization. We identify conditions on $\{M_k, k \geq 1\}$ and $\{\epsilon_k, k\geq 1\}$ that ensure almost sure convergence and convergence in $L_1$-norm, along with optimal iteration and work complexity rates. We illustrate the performance of RA with line-search quasi-Newton on an ill-conditioned least squares problem, as well as an image classification problem using a deep convolutional neural net.

Constrained and Composite Optimization via Adaptive Sampling Methods

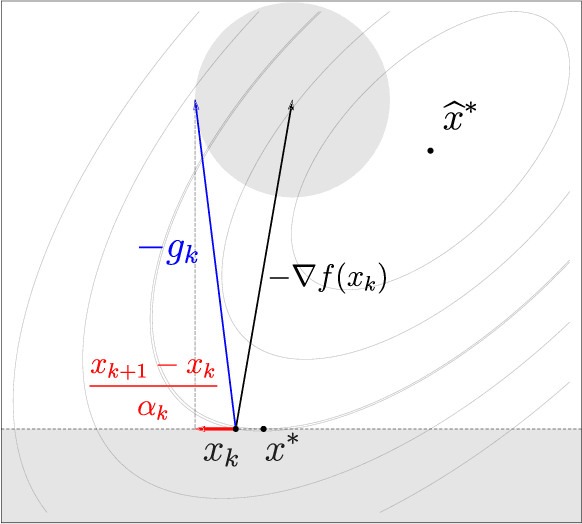
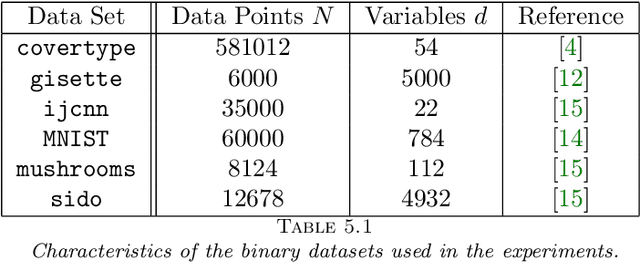
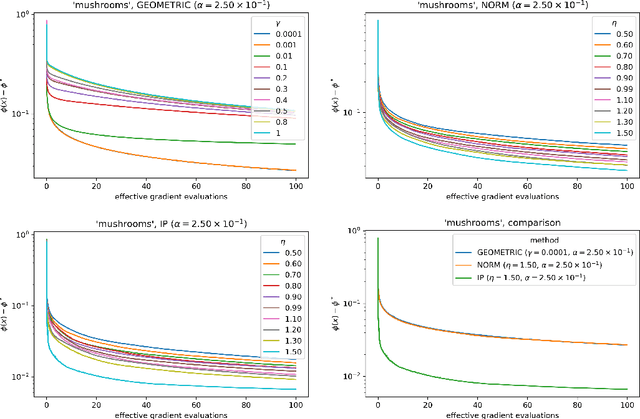
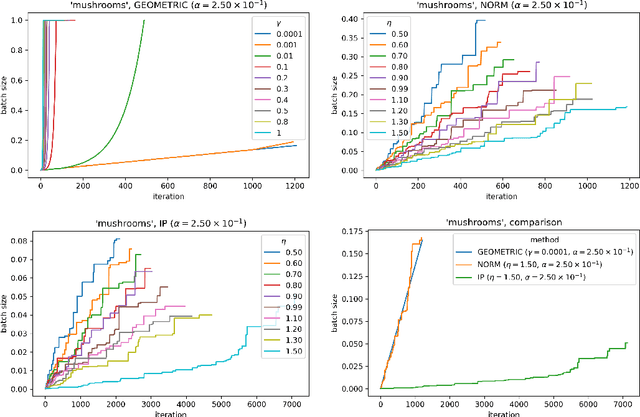
The motivation for this paper stems from the desire to develop an adaptive sampling method for solving constrained optimization problems in which the objective function is stochastic and the constraints are deterministic. The method proposed in this paper is a proximal gradient method that can also be applied to the composite optimization problem min f(x) + h(x), where f is stochastic and h is convex (but not necessarily differentiable). Adaptive sampling methods employ a mechanism for gradually improving the quality of the gradient approximation so as to keep computational cost to a minimum. The mechanism commonly employed in unconstrained optimization is no longer reliable in the constrained or composite optimization settings because it is based on pointwise decisions that cannot correctly predict the quality of the proximal gradient step. The method proposed in this paper measures the result of a complete step to determine if the gradient approximation is accurate enough; otherwise a more accurate gradient is generated and a new step is computed. Convergence results are established both for strongly convex and general convex f. Numerical experiments are presented to illustrate the practical behavior of the method.

Adaptive Sampling Quasi-Newton Methods for Derivative-Free Stochastic Optimization

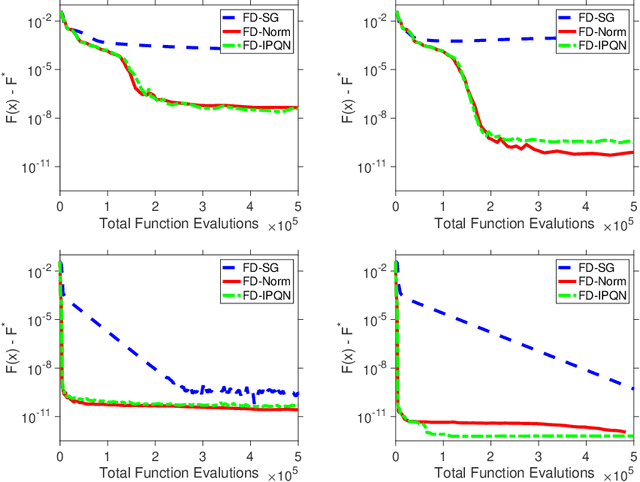
We consider stochastic zero-order optimization problems, which arise in settings from simulation optimization to reinforcement learning. We propose an adaptive sampling quasi-Newton method where we estimate the gradients of a stochastic function using finite differences within a common random number framework. We employ modified versions of a norm test and an inner product quasi-Newton test to control the sample sizes used in the stochastic approximations. We provide preliminary numerical experiments to illustrate potential performance benefits of the proposed method.

An Investigation of Newton-Sketch and Subsampled Newton Methods

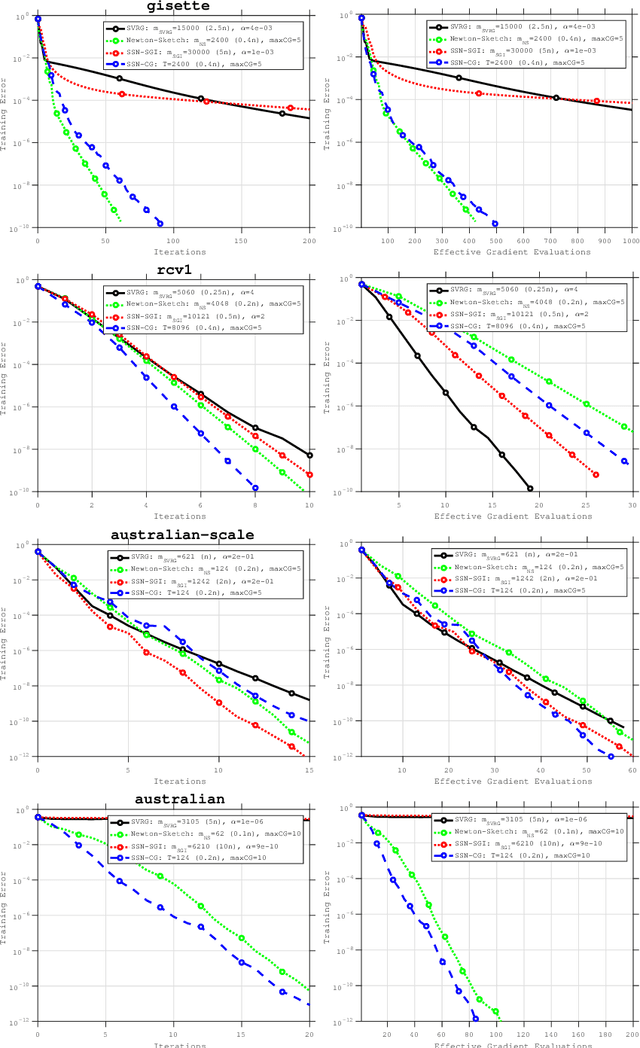
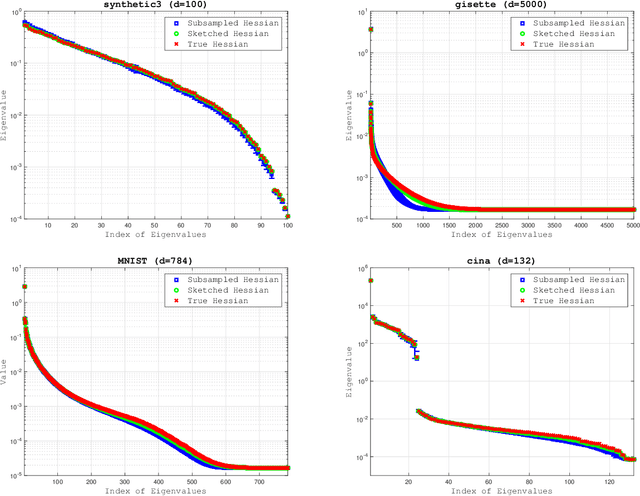
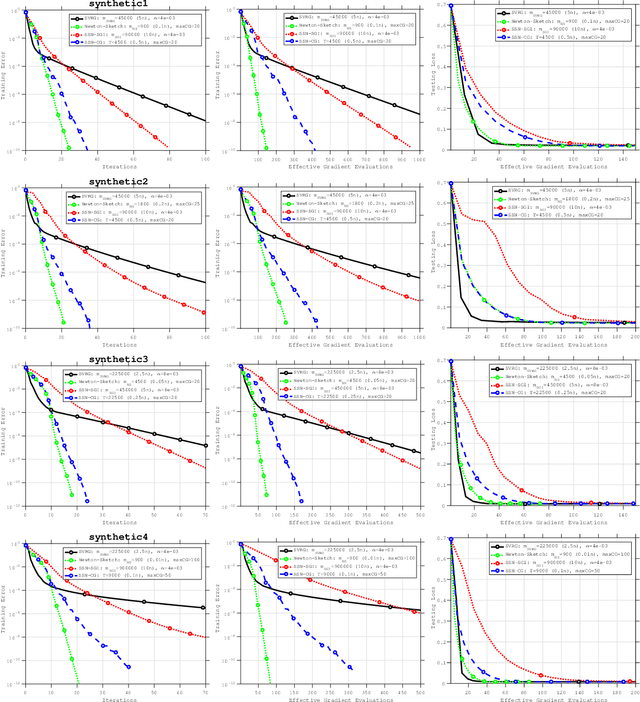
The concepts of sketching and subsampling have recently received much attention by the optimization and statistics communities. In this paper, we study Newton-Sketch and Subsampled Newton (SSN) methods for the finite-sum optimization problem. We consider practical versions of the two methods in which the Newton equations are solved approximately using the conjugate gradient (CG) method or a stochastic gradient iteration. We establish new complexity results for the SSN-CG method that exploit the spectral properties of CG. Controlled numerical experiments compare the relative strengths of Newton-Sketch and SSN methods and show that for many finite-sum problems, they are far more efficient than SVRG, a popular first-order method.

A Progressive Batching L-BFGS Method for Machine Learning

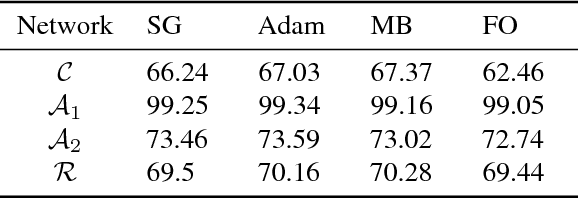
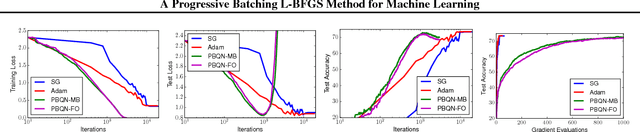
The standard L-BFGS method relies on gradient approximations that are not dominated by noise, so that search directions are descent directions, the line search is reliable, and quasi-Newton updating yields useful quadratic models of the objective function. All of this appears to call for a full batch approach, but since small batch sizes give rise to faster algorithms with better generalization properties, L-BFGS is currently not considered an algorithm of choice for large-scale machine learning applications. One need not, however, choose between the two extremes represented by the full batch or highly stochastic regimes, and may instead follow a progressive batching approach in which the sample size increases during the course of the optimization. In this paper, we present a new version of the L-BFGS algorithm that combines three basic components - progressive batching, a stochastic line search, and stable quasi-Newton updating - and that performs well on training logistic regression and deep neural networks. We provide supporting convergence theory for the method.

Adaptive Sampling Strategies for Stochastic Optimization

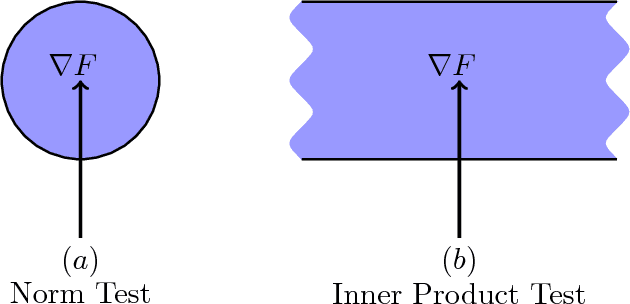
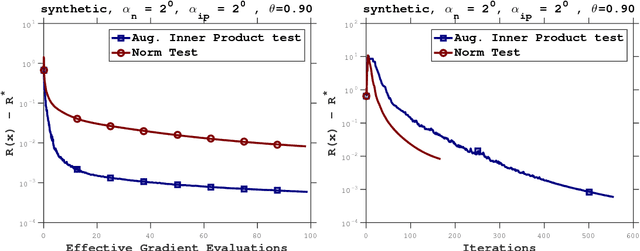
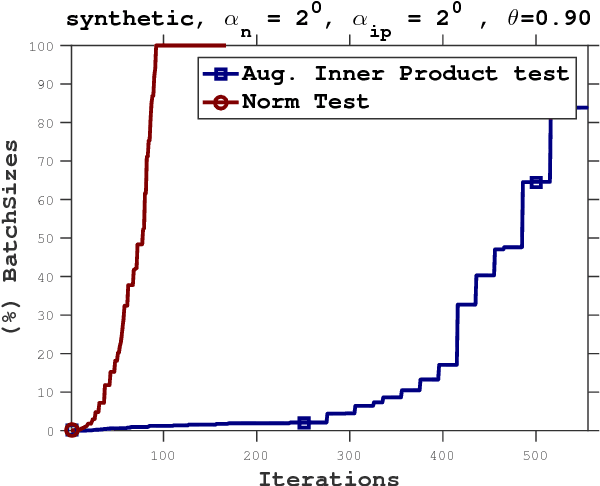
In this paper, we propose a stochastic optimization method that adaptively controls the sample size used in the computation of gradient approximations. Unlike other variance reduction techniques that either require additional storage or the regular computation of full gradients, the proposed method reduces variance by increasing the sample size as needed. The decision to increase the sample size is governed by an inner product test that ensures that search directions are descent directions with high probability. We show that the inner product test improves upon the well known norm test, and can be used as a basis for an algorithm that is globally convergent on nonconvex functions and enjoys a global linear rate of convergence on strongly convex functions. Numerical experiments on logistic regression problems illustrate the performance of the algorithm.