Adaptive Sampling Quasi-Newton Methods for Derivative-Free Stochastic Optimization
Paper and Code
Oct 29, 2019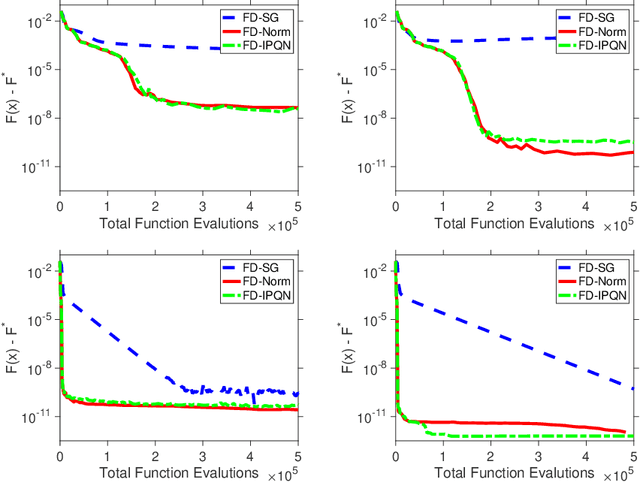
We consider stochastic zero-order optimization problems, which arise in settings from simulation optimization to reinforcement learning. We propose an adaptive sampling quasi-Newton method where we estimate the gradients of a stochastic function using finite differences within a common random number framework. We employ modified versions of a norm test and an inner product quasi-Newton test to control the sample sizes used in the stochastic approximations. We provide preliminary numerical experiments to illustrate potential performance benefits of the proposed method.
* 7 pages, NeurIPS workshop
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge