A framework for fully autonomous design of materials via multiobjective optimization and active learning: challenges and next steps

In order to deploy machine learning in a real-world self-driving laboratory where data acquisition is costly and there are multiple competing design criteria, systems need to be able to intelligently sample while balancing performance trade-offs and constraints. For these reasons, we present an active learning process based on multiobjective black-box optimization with continuously updated machine learning models. This workflow is built on open-source technologies for real-time data streaming and modular multiobjective optimization software development. We demonstrate a proof of concept for this workflow through the autonomous operation of a continuous-flow chemistry laboratory, which identifies ideal manufacturing conditions for the electrolyte 2,2,2-trifluoroethyl methyl carbonate.

Numerical evidence against advantage with quantum fidelity kernels on classical data

Quantum machine learning techniques are commonly considered one of the most promising candidates for demonstrating practical quantum advantage. In particular, quantum kernel methods have been demonstrated to be able to learn certain classically intractable functions efficiently if the kernel is well-aligned with the target function. In the more general case, quantum kernels are known to suffer from exponential "flattening" of the spectrum as the number of qubits grows, preventing generalization and necessitating the control of the inductive bias by hyperparameters. We show that the general-purpose hyperparameter tuning techniques proposed to improve the generalization of quantum kernels lead to the kernel becoming well-approximated by a classical kernel, removing the possibility of quantum advantage. We provide extensive numerical evidence for this phenomenon utilizing multiple previously studied quantum feature maps and both synthetic and real data. Our results show that unless novel techniques are developed to control the inductive bias of quantum kernels, they are unlikely to provide a quantum advantage on classical data.

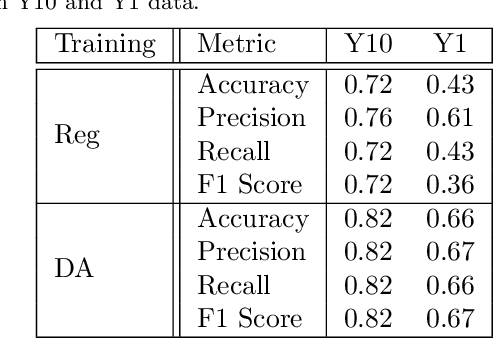
Semi-Supervised Domain Adaptation for Cross-Survey Galaxy Morphology Classification and Anomaly Detection

In the era of big astronomical surveys, our ability to leverage artificial intelligence algorithms simultaneously for multiple datasets will open new avenues for scientific discovery. Unfortunately, simply training a deep neural network on images from one data domain often leads to very poor performance on any other dataset. Here we develop a Universal Domain Adaptation method DeepAstroUDA, capable of performing semi-supervised domain alignment that can be applied to datasets with different types of class overlap. Extra classes can be present in any of the two datasets, and the method can even be used in the presence of unknown classes. For the first time, we demonstrate the successful use of domain adaptation on two very different observational datasets (from SDSS and DECaLS). We show that our method is capable of bridging the gap between two astronomical surveys, and also performs well for anomaly detection and clustering of unknown data in the unlabeled dataset. We apply our model to two examples of galaxy morphology classification tasks with anomaly detection: 1) classifying spiral and elliptical galaxies with detection of merging galaxies (three classes including one unknown anomaly class); 2) a more granular problem where the classes describe more detailed morphological properties of galaxies, with the detection of gravitational lenses (ten classes including one unknown anomaly class).

Bandwidth Enables Generalization in Quantum Kernel Models

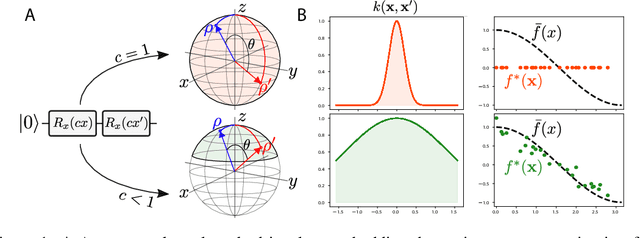
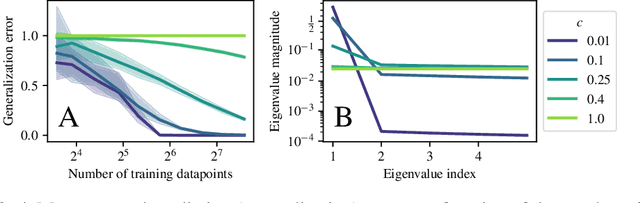
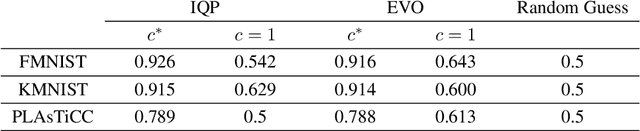
Quantum computers are known to provide speedups over classical state-of-the-art machine learning methods in some specialized settings. For example, quantum kernel methods have been shown to provide an exponential speedup on a learning version of the discrete logarithm problem. Understanding the generalization of quantum models is essential to realizing similar speedups on problems of practical interest. Recent results demonstrate that generalization is hindered by the exponential size of the quantum feature space. Although these results suggest that quantum models cannot generalize when the number of qubits is large, in this paper we show that these results rely on overly restrictive assumptions. We consider a wider class of models by varying a hyperparameter that we call quantum kernel bandwidth. We analyze the large-qubit limit and provide explicit formulas for the generalization of a quantum model that can be solved in closed form. Specifically, we show that changing the value of the bandwidth can take a model from provably not being able to generalize to any target function to good generalization for well-aligned targets. Our analysis shows how the bandwidth controls the spectrum of the kernel integral operator and thereby the inductive bias of the model. We demonstrate empirically that our theory correctly predicts how varying the bandwidth affects generalization of quantum models on challenging datasets, including those far outside our theoretical assumptions. We discuss the implications of our results for quantum advantage in machine learning.

DeepAdversaries: Examining the Robustness of Deep Learning Models for Galaxy Morphology Classification

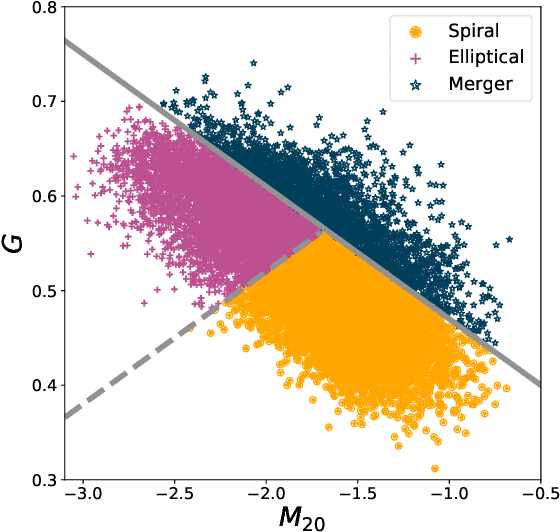
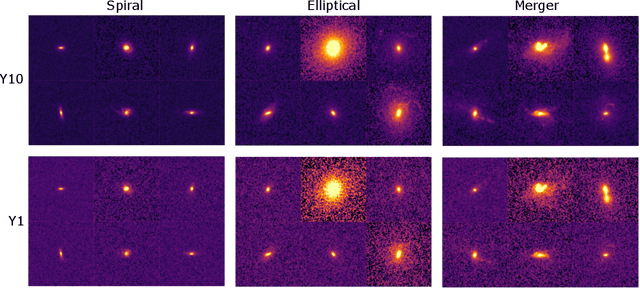
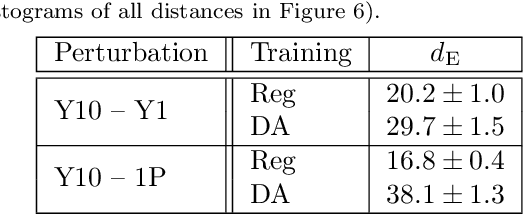
Data processing and analysis pipelines in cosmological survey experiments introduce data perturbations that can significantly degrade the performance of deep learning-based models. Given the increased adoption of supervised deep learning methods for processing and analysis of cosmological survey data, the assessment of data perturbation effects and the development of methods that increase model robustness are increasingly important. In the context of morphological classification of galaxies, we study the effects of perturbations in imaging data. In particular, we examine the consequences of using neural networks when training on baseline data and testing on perturbed data. We consider perturbations associated with two primary sources: 1) increased observational noise as represented by higher levels of Poisson noise and 2) data processing noise incurred by steps such as image compression or telescope errors as represented by one-pixel adversarial attacks. We also test the efficacy of domain adaptation techniques in mitigating the perturbation-driven errors. We use classification accuracy, latent space visualizations, and latent space distance to assess model robustness. Without domain adaptation, we find that processing pixel-level errors easily flip the classification into an incorrect class and that higher observational noise makes the model trained on low-noise data unable to classify galaxy morphologies. On the other hand, we show that training with domain adaptation improves model robustness and mitigates the effects of these perturbations, improving the classification accuracy by 23% on data with higher observational noise. Domain adaptation also increases by a factor of ~2.3 the latent space distance between the baseline and the incorrectly classified one-pixel perturbed image, making the model more robust to inadvertent perturbations.

Importance of Kernel Bandwidth in Quantum Machine Learning

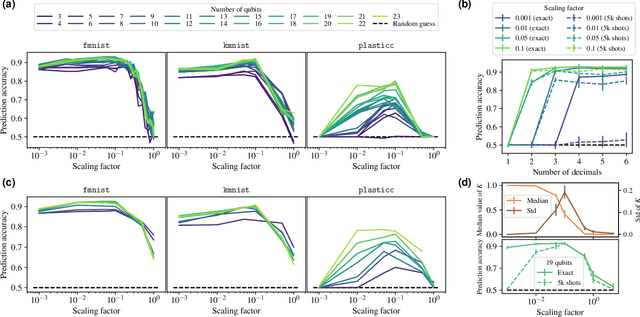
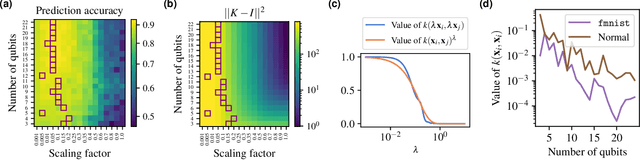
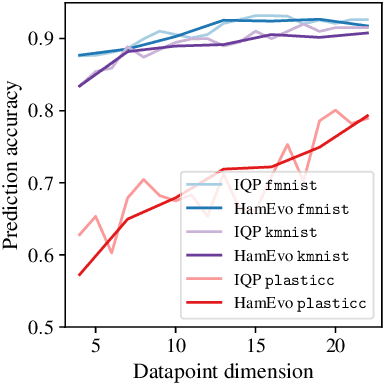
Quantum kernel methods are considered a promising avenue for applying quantum computers to machine learning problems. However, recent results overlook the central role hyperparameters play in determining the performance of machine learning methods. In this work we identify the hyperparameter controlling the bandwidth of a quantum kernel and show that it controls the expressivity of the resulting model. We use extensive numerical experiments with multiple quantum kernels and classical datasets to show consistent change in the model behavior from underfitting (bandwidth too large) to overfitting (bandwidth too small), with optimal generalization in between. We draw a connection between the bandwidth of classical and quantum kernels and show analogous behavior in both cases. Furthermore, we show that optimizing the bandwidth can help mitigate the exponential decay of kernel values with qubit count, which is the cause behind recent observations that the performance of quantum kernel methods decreases with qubit count. We reproduce these negative results and show that if the kernel bandwidth is optimized, the performance instead improves with growing qubit count and becomes competitive with the best classical methods.

Adaptive Sampling Quasi-Newton Methods for Zeroth-Order Stochastic Optimization

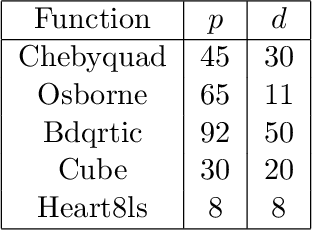
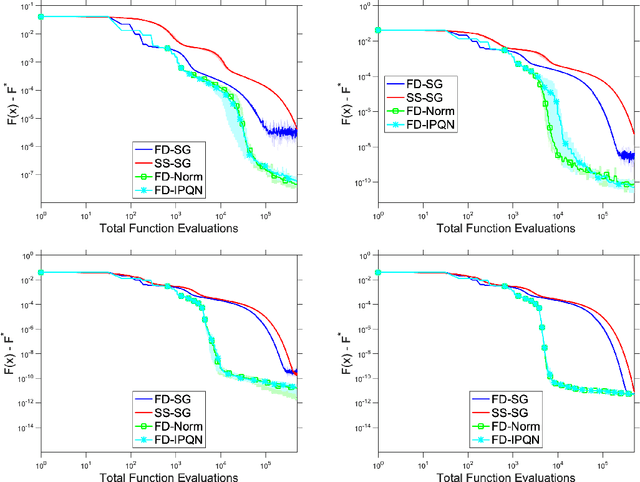
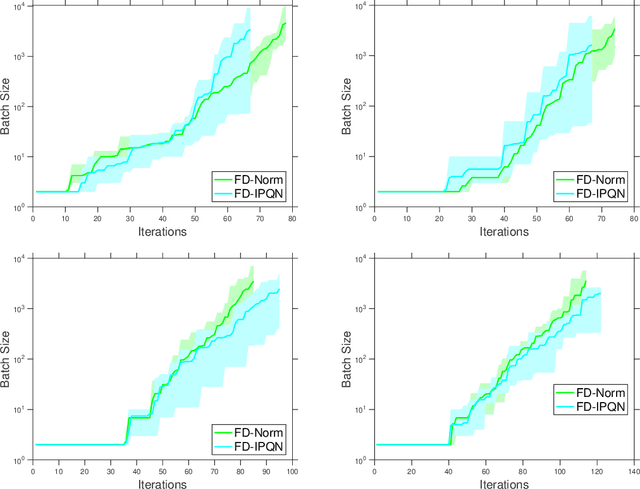
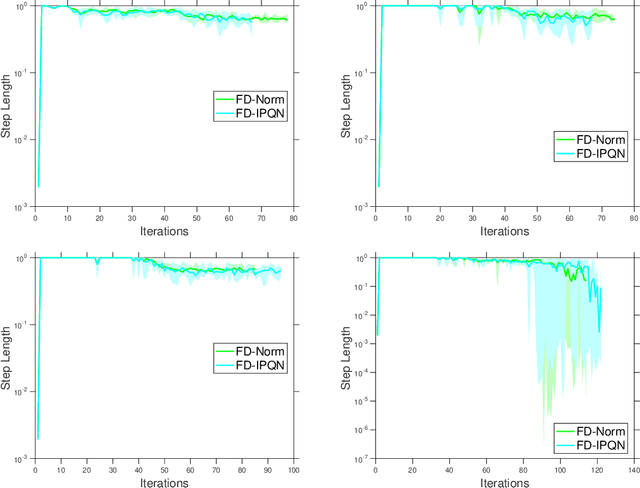
We consider unconstrained stochastic optimization problems with no available gradient information. Such problems arise in settings from derivative-free simulation optimization to reinforcement learning. We propose an adaptive sampling quasi-Newton method where we estimate the gradients of a stochastic function using finite differences within a common random number framework. We develop modified versions of a norm test and an inner product quasi-Newton test to control the sample sizes used in the stochastic approximations and provide global convergence results to the neighborhood of the optimal solution. We present numerical experiments on simulation optimization problems to illustrate the performance of the proposed algorithm. When compared with classical zeroth-order stochastic gradient methods, we observe that our strategies of adapting the sample sizes significantly improve performance in terms of the number of stochastic function evaluations required.

Randomized Algorithms for Scientific Computing (RASC)

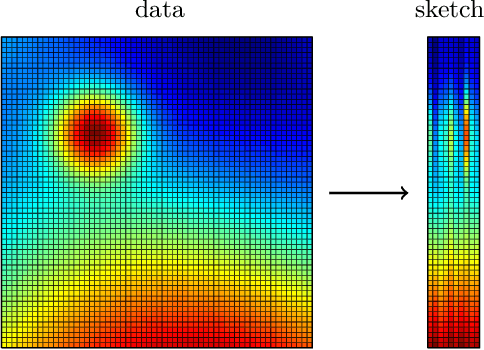
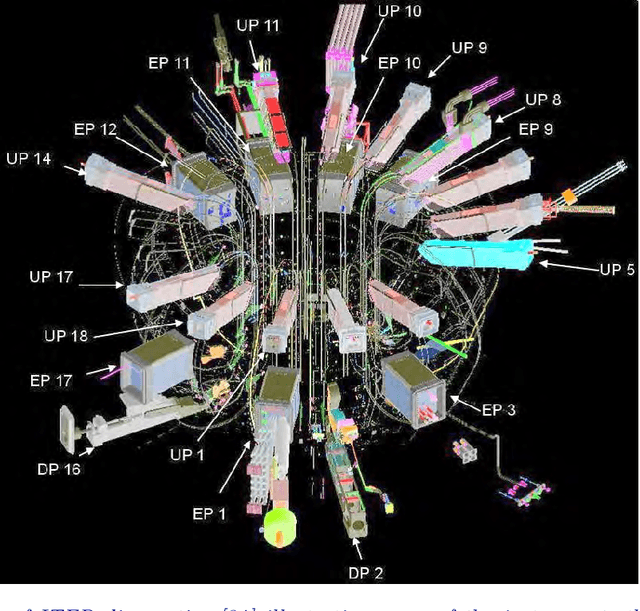
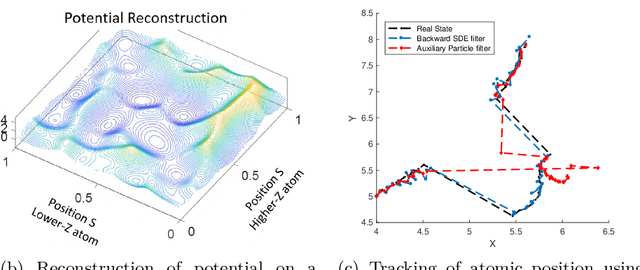
Randomized algorithms have propelled advances in artificial intelligence and represent a foundational research area in advancing AI for Science. Future advancements in DOE Office of Science priority areas such as climate science, astrophysics, fusion, advanced materials, combustion, and quantum computing all require randomized algorithms for surmounting challenges of complexity, robustness, and scalability. This report summarizes the outcomes of that workshop, "Randomized Algorithms for Scientific Computing (RASC)," held virtually across four days in December 2020 and January 2021.

Scalable Statistical Inference of Photometric Redshift via Data Subsampling

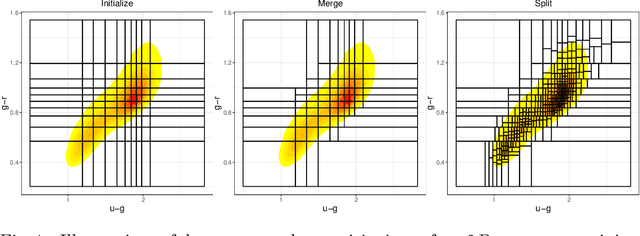
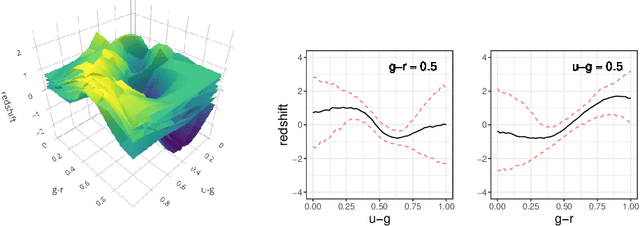
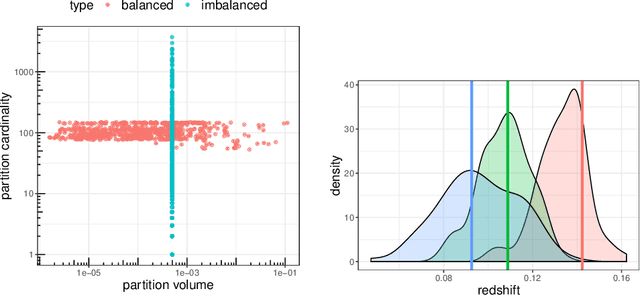
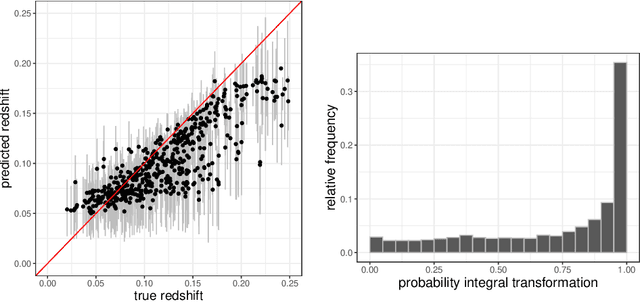
Handling big data has largely been a major bottleneck in traditional statistical models. Consequently, when accurate point prediction is the primary target, machine learning models are often preferred over their statistical counterparts for bigger problems. But full probabilistic statistical models often outperform other models in quantifying uncertainties associated with model predictions. We develop a data-driven statistical modeling framework that combines the uncertainties from an ensemble of statistical models learned on smaller subsets of data carefully chosen to account for imbalances in the input space. We demonstrate this method on a photometric redshift estimation problem in cosmology, which seeks to infer a distribution of the redshift -- the stretching effect in observing the light of far-away galaxies -- given multivariate color information observed for an object in the sky. Our proposed method performs balanced partitioning, graph-based data subsampling across the partitions, and training of an ensemble of Gaussian process models.

Adaptive Sampling Quasi-Newton Methods for Derivative-Free Stochastic Optimization

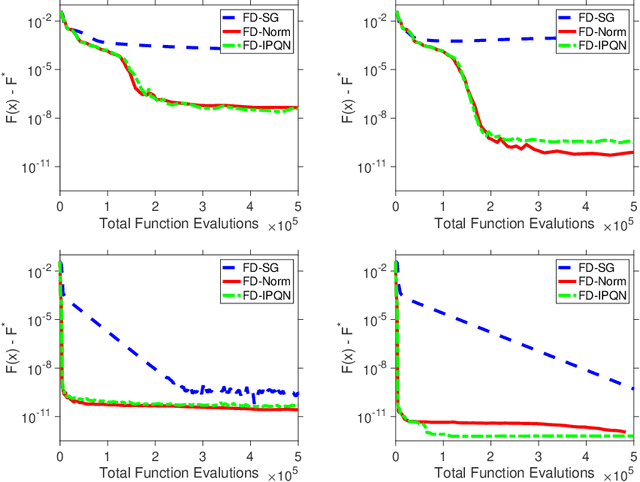
We consider stochastic zero-order optimization problems, which arise in settings from simulation optimization to reinforcement learning. We propose an adaptive sampling quasi-Newton method where we estimate the gradients of a stochastic function using finite differences within a common random number framework. We employ modified versions of a norm test and an inner product quasi-Newton test to control the sample sizes used in the stochastic approximations. We provide preliminary numerical experiments to illustrate potential performance benefits of the proposed method.