Gearing Gaussian process modeling and sequential design towards stochastic simulators

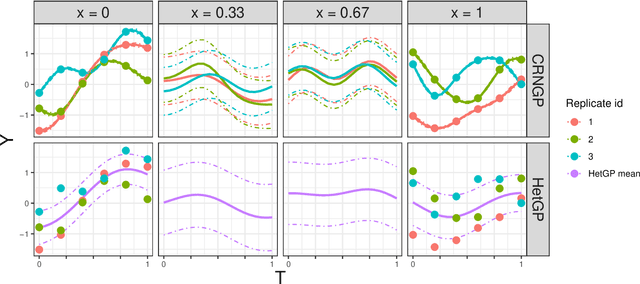
This chapter presents specific aspects of Gaussian process modeling in the presence of complex noise. Starting from the standard homoscedastic model, various generalizations from the literature are presented: input varying noise variance, non-Gaussian noise, or quantile modeling. These approaches are compared in terms of goal, data availability and inference procedure. A distinction is made between methods depending on their handling of repeated observations at the same location, also called replication. The chapter concludes with the corresponding adaptations of the sequential design procedures. These are illustrated in an example from epidemiology.

Trajectory-oriented optimization of stochastic epidemiological models

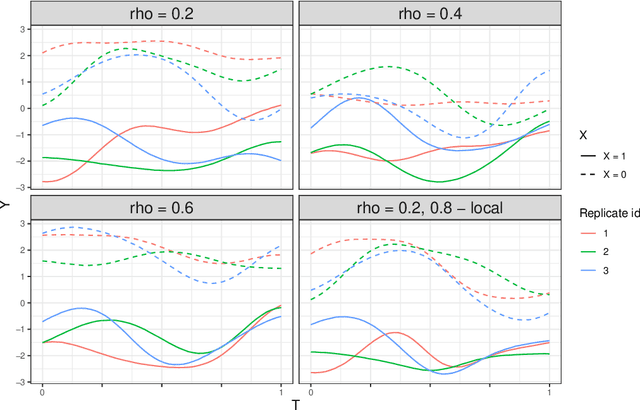
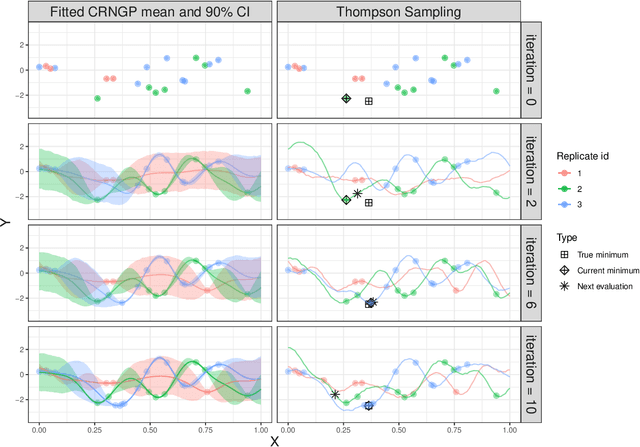
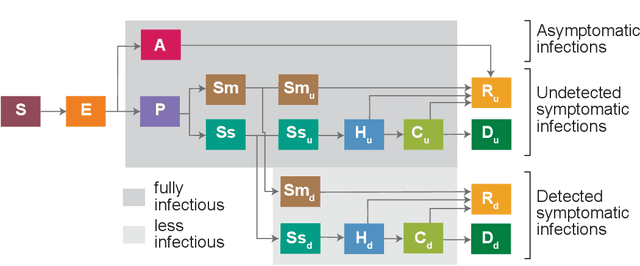
Epidemiological models must be calibrated to ground truth for downstream tasks such as producing forward projections or running what-if scenarios. The meaning of calibration changes in case of a stochastic model since output from such a model is generally described via an ensemble or a distribution. Each member of the ensemble is usually mapped to a random number seed (explicitly or implicitly). With the goal of finding not only the input parameter settings but also the random seeds that are consistent with the ground truth, we propose a class of Gaussian process (GP) surrogates along with an optimization strategy based on Thompson sampling. This Trajectory Oriented Optimization (TOO) approach produces actual trajectories close to the empirical observations instead of a set of parameter settings where only the mean simulation behavior matches with the ground truth.

Scalable Statistical Inference of Photometric Redshift via Data Subsampling

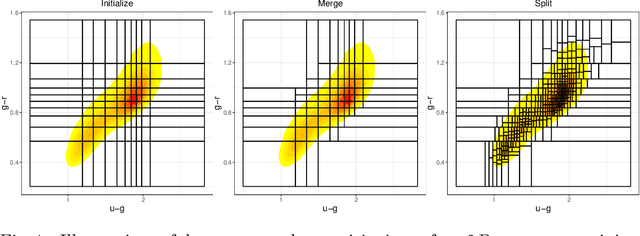
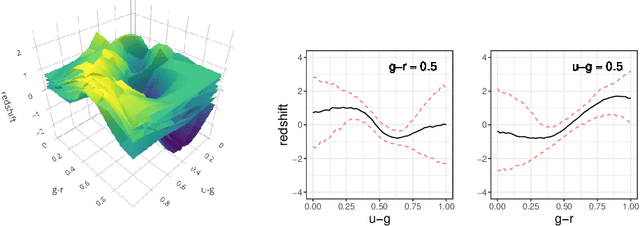
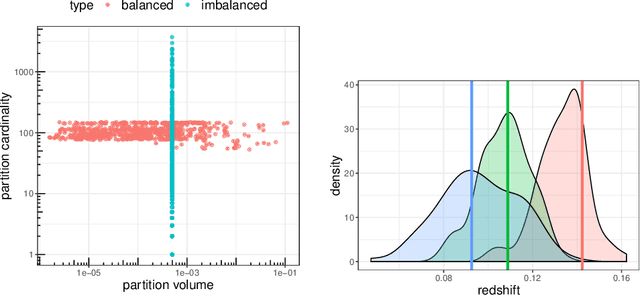
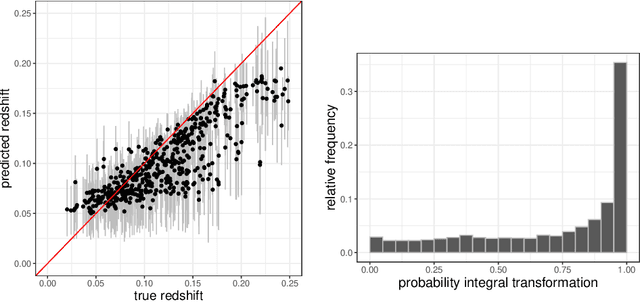
Handling big data has largely been a major bottleneck in traditional statistical models. Consequently, when accurate point prediction is the primary target, machine learning models are often preferred over their statistical counterparts for bigger problems. But full probabilistic statistical models often outperform other models in quantifying uncertainties associated with model predictions. We develop a data-driven statistical modeling framework that combines the uncertainties from an ensemble of statistical models learned on smaller subsets of data carefully chosen to account for imbalances in the input space. We demonstrate this method on a photometric redshift estimation problem in cosmology, which seeks to infer a distribution of the redshift -- the stretching effect in observing the light of far-away galaxies -- given multivariate color information observed for an object in the sky. Our proposed method performs balanced partitioning, graph-based data subsampling across the partitions, and training of an ensemble of Gaussian process models.