Advancing calibration for stochastic agent-based models in epidemiology with Stein variational inference and Gaussian process surrogates

Accurate calibration of stochastic agent-based models (ABMs) in epidemiology is crucial to make them useful in public health policy decisions and interventions. Traditional calibration methods, e.g., Markov Chain Monte Carlo (MCMC), that yield a probability density function for the parameters being calibrated, are often computationally expensive. When applied to ABMs which are highly parametrized, the calibration process becomes computationally infeasible. This paper investigates the utility of Stein Variational Inference (SVI) as an alternative calibration technique for stochastic epidemiological ABMs approximated by Gaussian process (GP) surrogates. SVI leverages gradient information to iteratively update a set of particles in the space of parameters being calibrated, offering potential advantages in scalability and efficiency for high-dimensional ABMs. The ensemble of particles yields a joint probability density function for the parameters and serves as the calibration. We compare the performance of SVI and MCMC in calibrating CityCOVID, a stochastic epidemiological ABM, focusing on predictive accuracy and calibration effectiveness. Our results demonstrate that SVI maintains predictive accuracy and calibration effectiveness comparable to MCMC, making it a viable alternative for complex epidemiological models. We also present the practical challenges of using a gradient-based calibration such as SVI which include careful tuning of hyperparameters and monitoring of the particle dynamics.

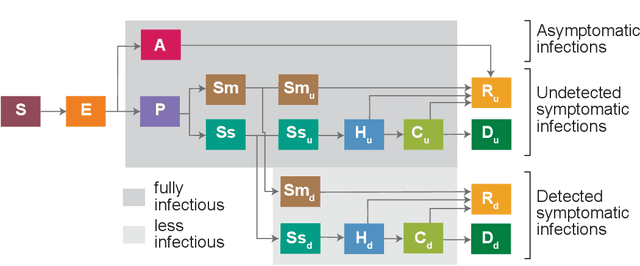
Bayesian calibration of stochastic agent based model via random forest

Agent-based models (ABM) provide an excellent framework for modeling outbreaks and interventions in epidemiology by explicitly accounting for diverse individual interactions and environments. However, these models are usually stochastic and highly parametrized, requiring precise calibration for predictive performance. When considering realistic numbers of agents and properly accounting for stochasticity, this high dimensional calibration can be computationally prohibitive. This paper presents a random forest based surrogate modeling technique to accelerate the evaluation of ABMs and demonstrates its use to calibrate an epidemiological ABM named CityCOVID via Markov chain Monte Carlo (MCMC). The technique is first outlined in the context of CityCOVID's quantities of interest, namely hospitalizations and deaths, by exploring dimensionality reduction via temporal decomposition with principal component analysis (PCA) and via sensitivity analysis. The calibration problem is then presented and samples are generated to best match COVID-19 hospitalization and death numbers in Chicago from March to June in 2020. These results are compared with previous approximate Bayesian calibration (IMABC) results and their predictive performance is analyzed showing improved performance with a reduction in computation.

Trajectory-oriented optimization of stochastic epidemiological models

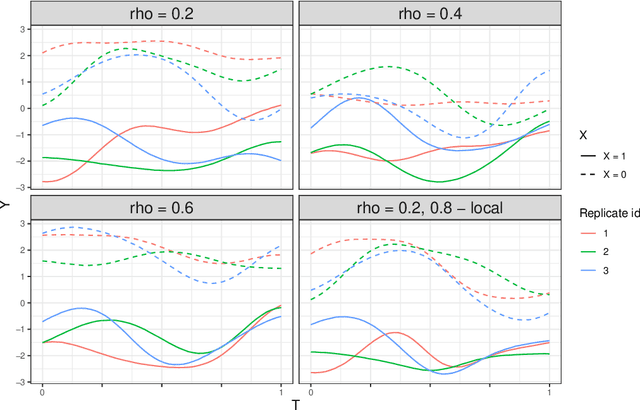
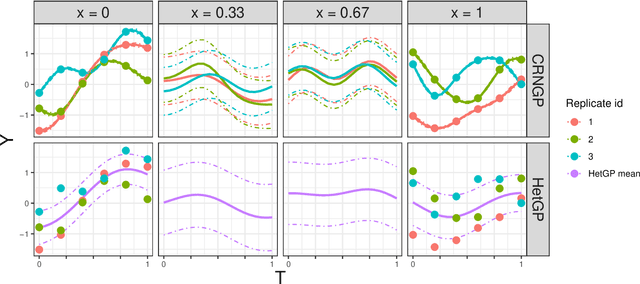
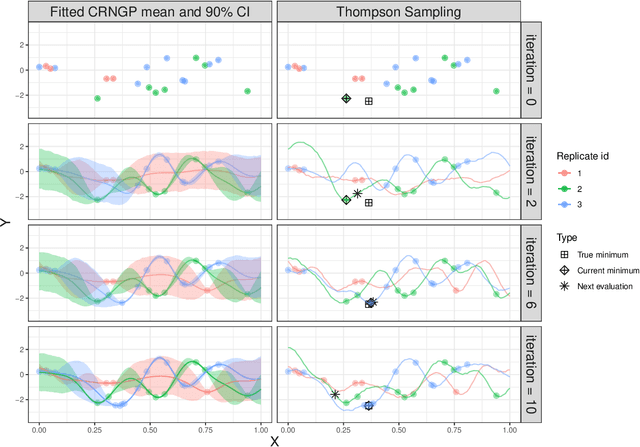
Epidemiological models must be calibrated to ground truth for downstream tasks such as producing forward projections or running what-if scenarios. The meaning of calibration changes in case of a stochastic model since output from such a model is generally described via an ensemble or a distribution. Each member of the ensemble is usually mapped to a random number seed (explicitly or implicitly). With the goal of finding not only the input parameter settings but also the random seeds that are consistent with the ground truth, we propose a class of Gaussian process (GP) surrogates along with an optimization strategy based on Thompson sampling. This Trajectory Oriented Optimization (TOO) approach produces actual trajectories close to the empirical observations instead of a set of parameter settings where only the mean simulation behavior matches with the ground truth.

A portfolio approach to massively parallel Bayesian optimization

One way to reduce the time of conducting optimization studies is to evaluate designs in parallel rather than just one-at-a-time. For expensive-to-evaluate black-boxes, batch versions of Bayesian optimization have been proposed. They work by building a surrogate model of the black-box that can be used to select the designs to evaluate efficiently via an infill criterion. Still, with higher levels of parallelization becoming available, the strategies that work for a few tens of parallel evaluations become limiting, in particular due to the complexity of selecting more evaluations. It is even more crucial when the black-box is noisy, necessitating more evaluations as well as repeating experiments. Here we propose a scalable strategy that can keep up with massive batching natively, focused on the exploration/exploitation trade-off and a portfolio allocation. We compare the approach with related methods on deterministic and noisy functions, for mono and multiobjective optimization tasks. These experiments show similar or better performance than existing methods, while being orders of magnitude faster.