Spatio-Temporal Surrogates for Interaction of a Jet with High Explosives: Part II -- Clustering Extremely High-Dimensional Grid-Based Data

Building an accurate surrogate model for the spatio-temporal outputs of a computer simulation is a challenging task. A simple approach to improve the accuracy of the surrogate is to cluster the outputs based on similarity and build a separate surrogate model for each cluster. This clustering is relatively straightforward when the output at each time step is of moderate size. However, when the spatial domain is represented by a large number of grid points, numbering in the millions, the clustering of the data becomes more challenging. In this report, we consider output data from simulations of a jet interacting with high explosives. These data are available on spatial domains of different sizes, at grid points that vary in their spatial coordinates, and in a format that distributes the output across multiple files at each time step of the simulation. We first describe how we bring these data into a consistent format prior to clustering. Borrowing the idea of random projections from data mining, we reduce the dimension of our data by a factor of thousand, making it possible to use the iterative k-means method for clustering. We show how we can use the randomness of both the random projections, and the choice of initial centroids in k-means clustering, to determine the number of clusters in our data set. Our approach makes clustering of extremely high dimensional data tractable, generating meaningful cluster assignments for our problem, despite the approximation introduced in the random projections.

Spatio-Temporal Surrogates for Interaction of a Jet with High Explosives: Part I -- Analysis with a Small Sample Size

Computer simulations, especially of complex phenomena, can be expensive, requiring high-performance computing resources. Often, to understand a phenomenon, multiple simulations are run, each with a different set of simulation input parameters. These data are then used to create an interpolant, or surrogate, relating the simulation outputs to the corresponding inputs. When the inputs and outputs are scalars, a simple machine learning model can suffice. However, when the simulation outputs are vector valued, available at locations in two or three spatial dimensions, often with a temporal component, creating a surrogate is more challenging. In this report, we use a two-dimensional problem of a jet interacting with high explosives to understand how we can build high-quality surrogates. The characteristics of our data set are unique - the vector-valued outputs from each simulation are available at over two million spatial locations; each simulation is run for a relatively small number of time steps; the size of the computational domain varies with each simulation; and resource constraints limit the number of simulations we can run. We show how we analyze these extremely large data-sets, set the parameters for the algorithms used in the analysis, and use simple ways to improve the accuracy of the spatio-temporal surrogates without substantially increasing the number of simulations required.

Data Mining for Faster, Interpretable Solutions to Inverse Problems: A Case Study Using Additive Manufacturing

Solving inverse problems, where we find the input values that result in desired values of outputs, can be challenging. The solution process is often computationally expensive and it can be difficult to interpret the solution in high-dimensional input spaces. In this paper, we use a problem from additive manufacturing to address these two issues with the intent of making it easier to solve inverse problems and exploit their results. First, focusing on Gaussian process surrogates that are used to solve inverse problems, we describe how a simple modification to the idea of tapering can substantially speed up the surrogate without losing accuracy in prediction. Second, we demonstrate that Kohonen self-organizing maps can be used to visualize and interpret the solution to the inverse problem in the high-dimensional input space. For our data set, as not all input dimensions are equally important, we show that using weighted distances results in a better organized map that makes the relationships among the inputs obvious.

Intelligent sampling for surrogate modeling, hyperparameter optimization, and data analysis

Sampling techniques are used in many fields, including design of experiments, image processing, and graphics. The techniques in each field are designed to meet the constraints specific to that field such as uniform coverage of the range of each dimension or random samples that are at least a certain distance apart from each other. When an application imposes new constraints, for example, by requiring samples in a non-rectangular domain or the addition of new samples to an existing set, a common solution is to modify the algorithm currently in use, often with less than satisfactory results. As an alternative, we propose the concept of intelligent sampling, where we devise algorithms specifically tailored to meet our sampling needs, either by creating new algorithms or by modifying suitable algorithms from other fields. Surprisingly, both qualitative and quantitative comparisons indicate that some relatively simple algorithms can be easily modified to meet the many sampling requirements of surrogate modeling, hyperparameter optimization, and data analysis; these algorithms outperform their more sophisticated counterparts currently in use, resulting in better use of time and computer resources.

Classification of Orbits in Poincaré Maps using Machine Learning

Poincar\'e plots, also called Poincar\'e maps, are used by plasma physicists to understand the behavior of magnetically confined plasma in numerical simulations of a tokamak. These plots are created by the intersection of field lines with a two-dimensional poloidal plane that is perpendicular to the axis of the torus representing the tokamak. A plot is composed of multiple orbits, each created by a different field line as it goes around the torus. Each orbit can have one of four distinct shapes, or classes, that indicate changes in the topology of the magnetic fields confining the plasma. Given the (x,y) coordinates of the points that form an orbit, the analysis task is to assign a class to the orbit, a task that appears ideally suited for a machine learning approach. In this paper, we describe how we overcame two major challenges in solving this problem - creating a high-quality training set, with few mislabeled orbits, and converting the coordinates of the points into features that are discriminating, despite the variation within the orbits of a class and the apparent similarities between orbits of different classes. Our automated approach is not only more objective and accurate than visual classification, but is also less tedious, making it easier for plasma physicists to analyze the topology of magnetic fields from numerical simulations of the tokamak.

Randomized Algorithms for Scientific Computing (RASC)

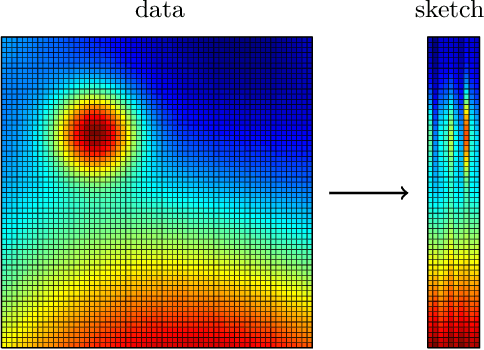
Randomized algorithms have propelled advances in artificial intelligence and represent a foundational research area in advancing AI for Science. Future advancements in DOE Office of Science priority areas such as climate science, astrophysics, fusion, advanced materials, combustion, and quantum computing all require randomized algorithms for surmounting challenges of complexity, robustness, and scalability. This report summarizes the outcomes of that workshop, "Randomized Algorithms for Scientific Computing (RASC)," held virtually across four days in December 2020 and January 2021.