Randomized Algorithms for Scientific Computing (RASC)

Randomized algorithms have propelled advances in artificial intelligence and represent a foundational research area in advancing AI for Science. Future advancements in DOE Office of Science priority areas such as climate science, astrophysics, fusion, advanced materials, combustion, and quantum computing all require randomized algorithms for surmounting challenges of complexity, robustness, and scalability. This report summarizes the outcomes of that workshop, "Randomized Algorithms for Scientific Computing (RASC)," held virtually across four days in December 2020 and January 2021.

A Survey of Constrained Gaussian Process Regression: Approaches and Implementation Challenges

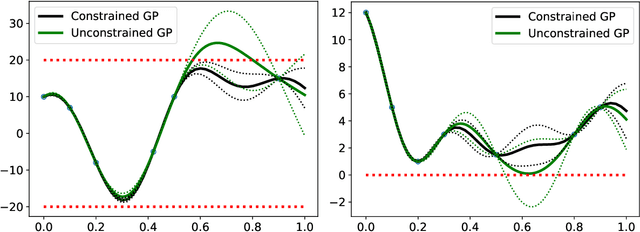
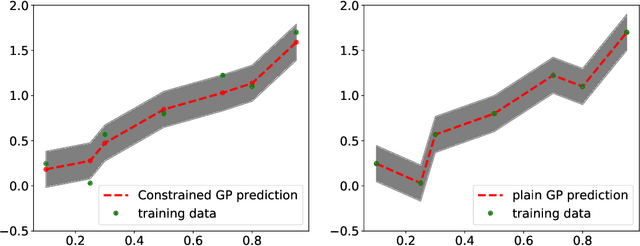
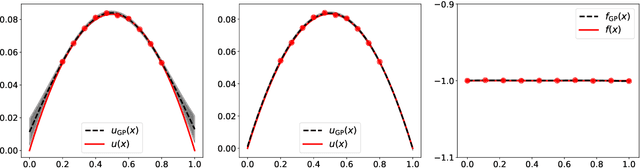
Gaussian process regression is a popular Bayesian framework for surrogate modeling of expensive data sources. As part of a broader effort in scientific machine learning, many recent works have incorporated physical constraints or other a priori information within Gaussian process regression to supplement limited data and regularize the behavior of the model. We provide an overview and survey of several classes of Gaussian process constraints, including positivity or bound constraints, monotonicity and convexity constraints, differential equation constraints provided by linear PDEs, and boundary condition constraints. We compare the strategies behind each approach as well as the differences in implementation, concluding with a discussion of the computational challenges introduced by constraints.

Data-driven learning of non-autonomous systems

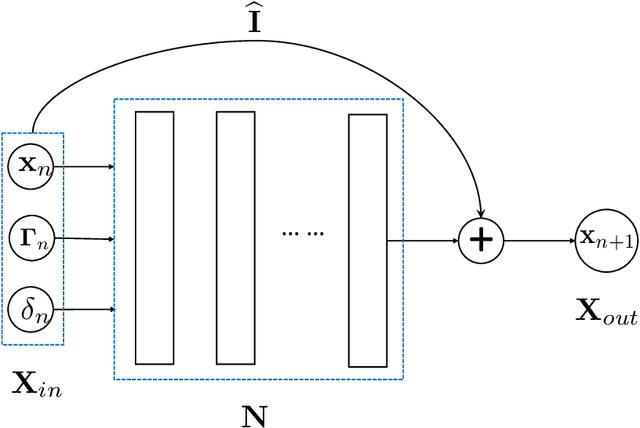
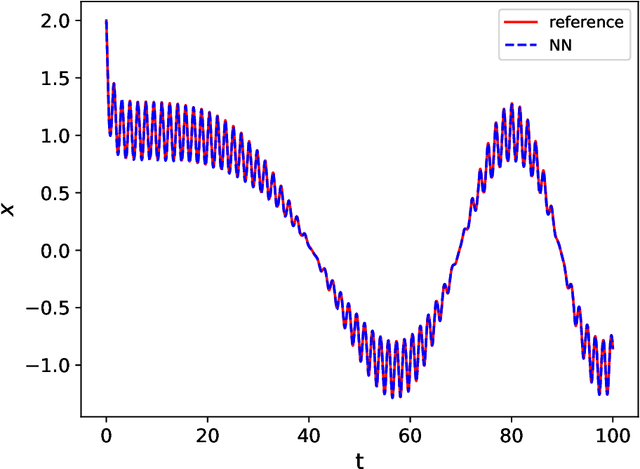
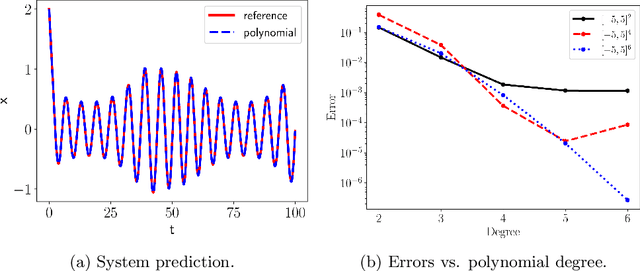
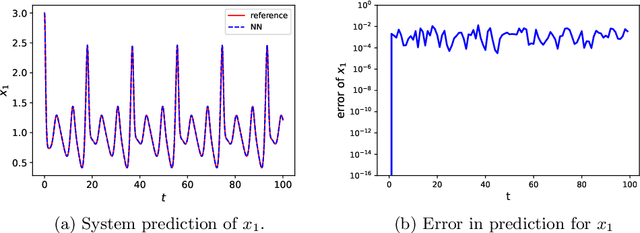
We present a numerical framework for recovering unknown non-autonomous dynamical systems with time-dependent inputs. To circumvent the difficulty presented by the non-autonomous nature of the system, our method transforms the solution state into piecewise integration of the system over a discrete set of time instances. The time-dependent inputs are then locally parameterized by using a proper model, for example, polynomial regression, in the pieces determined by the time instances. This transforms the original system into a piecewise parametric system that is locally time invariant. We then design a deep neural network structure to learn the local models. Once the network model is constructed, it can be iteratively used over time to conduct global system prediction. We provide theoretical analysis of our algorithm and present a number of numerical examples to demonstrate the effectiveness of the method.