DUE: A Deep Learning Framework and Library for Modeling Unknown Equations

Equations, particularly differential equations, are fundamental for understanding natural phenomena and predicting complex dynamics across various scientific and engineering disciplines. However, the governing equations for many complex systems remain unknown due to intricate underlying mechanisms. Recent advancements in machine learning and data science offer a new paradigm for modeling unknown equations from measurement or simulation data. This paradigm shift, known as data-driven discovery or modeling, stands at the forefront of AI for science, with significant progress made in recent years. In this paper, we introduce a systematic framework for data-driven modeling of unknown equations using deep learning. This versatile framework is capable of learning unknown ODEs, PDEs, DAEs, IDEs, SDEs, reduced or partially observed systems, and non-autonomous differential equations. Based on this framework, we have developed Deep Unknown Equations (DUE), an open-source software package designed to facilitate the data-driven modeling of unknown equations using modern deep learning techniques. DUE serves as an educational tool for classroom instruction, enabling students and newcomers to gain hands-on experience with differential equations, data-driven modeling, and contemporary deep learning approaches such as FNN, ResNet, generalized ResNet, operator semigroup networks (OSG-Net), and Transformers. Additionally, DUE is a versatile and accessible toolkit for researchers across various scientific and engineering fields. It is applicable not only for learning unknown equations from data but also for surrogate modeling of known, yet complex, equations that are costly to solve using traditional numerical methods. We provide detailed descriptions of DUE and demonstrate its capabilities through diverse examples, which serve as templates that can be easily adapted for other applications.

Multi-fidelity Parameter Estimation Using Conditional Diffusion Models

We present a multi-fidelity method for uncertainty quantification of parameter estimates in complex systems, leveraging generative models trained to sample the target conditional distribution. In the Bayesian inference setting, traditional parameter estimation methods rely on repeated simulations of potentially expensive forward models to determine the posterior distribution of the parameter values, which may result in computationally intractable workflows. Furthermore, methods such as Markov Chain Monte Carlo (MCMC) necessitate rerunning the entire algorithm for each new data observation, further increasing the computational burden. Hence, we propose a novel method for efficiently obtaining posterior distributions of parameter estimates for high-fidelity models given data observations of interest. The method first constructs a low-fidelity, conditional generative model capable of amortized Bayesian inference and hence rapid posterior density approximation over a wide-range of data observations. When higher accuracy is needed for a specific data observation, the method employs adaptive refinement of the density approximation. It uses outputs from the low-fidelity generative model to refine the parameter sampling space, ensuring efficient use of the computationally expensive high-fidelity solver. Subsequently, a high-fidelity, unconditional generative model is trained to achieve greater accuracy in the target posterior distribution. Both low- and high- fidelity generative models enable efficient sampling from the target posterior and do not require repeated simulation of the high-fidelity forward model. We demonstrate the effectiveness of the proposed method on several numerical examples, including cases with multi-modal densities, as well as an application in plasma physics for a runaway electron simulation model.

Deep learning for model correction of dynamical systems with data scarcity

We present a deep learning framework for correcting existing dynamical system models utilizing only a scarce high-fidelity data set. In many practical situations, one has a low-fidelity model that can capture the dynamics reasonably well but lacks high resolution, due to the inherent limitation of the model and the complexity of the underlying physics. When high resolution data become available, it is natural to seek model correction to improve the resolution of the model predictions. We focus on the case when the amount of high-fidelity data is so small that most of the existing data driven modeling methods cannot be applied. In this paper, we address these challenges with a model-correction method which only requires a scarce high-fidelity data set. Our method first seeks a deep neural network (DNN) model to approximate the existing low-fidelity model. By using the scarce high-fidelity data, the method then corrects the DNN model via transfer learning (TL). After TL, an improved DNN model with high prediction accuracy to the underlying dynamics is obtained. One distinct feature of the propose method is that it does not assume a specific form of the model correction terms. Instead, it offers an inherent correction to the low-fidelity model via TL. A set of numerical examples are presented to demonstrate the effectiveness of the proposed method.

A Training-Free Conditional Diffusion Model for Learning Stochastic Dynamical Systems

This study introduces a training-free conditional diffusion model for learning unknown stochastic differential equations (SDEs) using data. The proposed approach addresses key challenges in computational efficiency and accuracy for modeling SDEs by utilizing a score-based diffusion model to approximate their stochastic flow map. Unlike the existing methods, this technique is based on an analytically derived closed-form exact score function, which can be efficiently estimated by Monte Carlo method using the trajectory data, and eliminates the need for neural network training to learn the score function. By generating labeled data through solving the corresponding reverse ordinary differential equation, the approach enables supervised learning of the flow map. Extensive numerical experiments across various SDE types, including linear, nonlinear, and multi-dimensional systems, demonstrate the versatility and effectiveness of the method. The learned models exhibit significant improvements in predicting both short-term and long-term behaviors of unknown stochastic systems, often surpassing baseline methods like GANs in estimating drift and diffusion coefficients.

Chebyshev Feature Neural Network for Accurate Function Approximation

We present a new Deep Neural Network (DNN) architecture capable of approximating functions up to machine accuracy. Termed Chebyshev Feature Neural Network (CFNN), the new structure employs Chebyshev functions with learnable frequencies as the first hidden layer, followed by the standard fully connected hidden layers. The learnable frequencies of the Chebyshev layer are initialized with exponential distributions to cover a wide range of frequencies. Combined with a multi-stage training strategy, we demonstrate that this CFNN structure can achieve machine accuracy during training. A comprehensive set of numerical examples for dimensions up to $20$ are provided to demonstrate the effectiveness and scalability of the method.

Data-driven Effective Modeling of Multiscale Stochastic Dynamical Systems

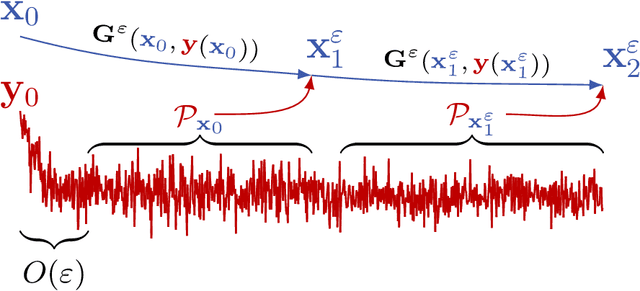
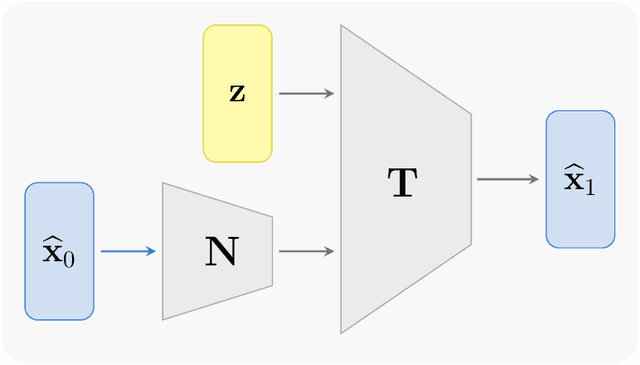
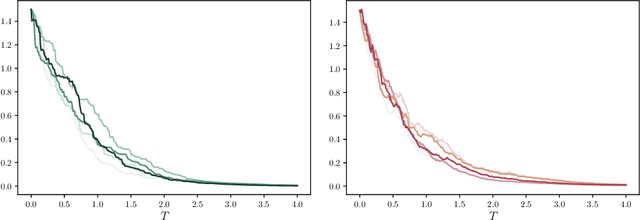
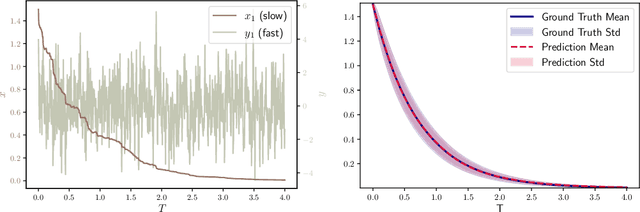
We present a numerical method for learning the dynamics of slow components of unknown multiscale stochastic dynamical systems. While the governing equations of the systems are unknown, bursts of observation data of the slow variables are available. By utilizing the observation data, our proposed method is capable of constructing a generative stochastic model that can accurately capture the effective dynamics of the slow variables in distribution. We present a comprehensive set of numerical examples to demonstrate the performance of the proposed method.

Dimension-reduced Reconstruction Map Learning for Parameter Estimation in Likelihood-Free Inference Problems

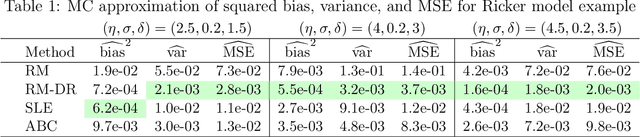
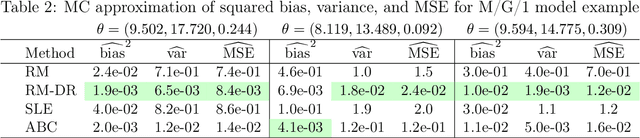
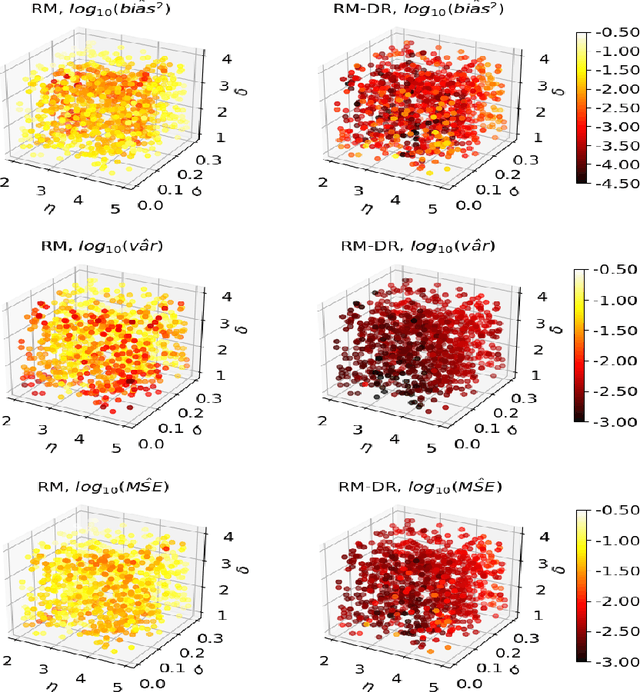
Many application areas rely on models that can be readily simulated but lack a closed-form likelihood, or an accurate approximation under arbitrary parameter values. Existing parameter estimation approaches in this setting are generally approximate. Recent work on using neural network models to reconstruct the mapping from the data space to the parameters from a set of synthetic parameter-data pairs suffers from the curse of dimensionality, resulting in inaccurate estimation as the data size grows. We propose a dimension-reduced approach to likelihood-free estimation which combines the ideas of reconstruction map estimation with dimension-reduction approaches based on subject-specific knowledge. We examine the properties of reconstruction map estimation with and without dimension reduction and explore the trade-off between approximation error due to information loss from reducing the data dimension and approximation error. Numerical examples show that the proposed approach compares favorably with reconstruction map estimation, approximate Bayesian computation, and synthetic likelihood estimation.

Modeling Unknown Stochastic Dynamical System via Autoencoder

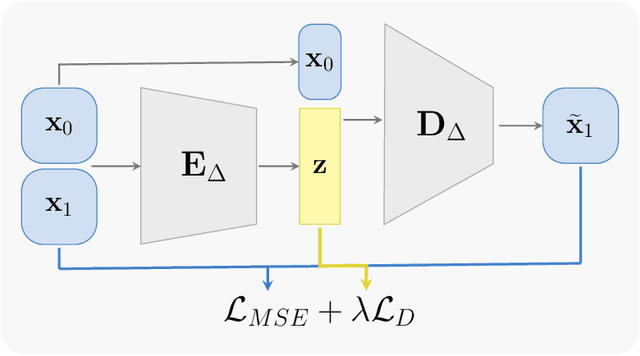
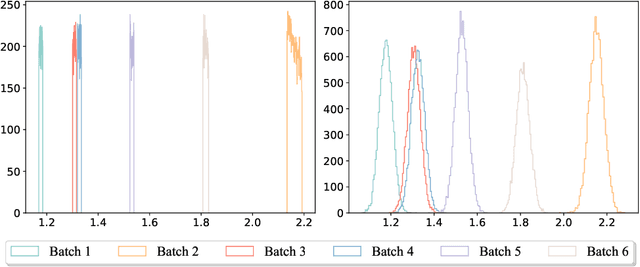
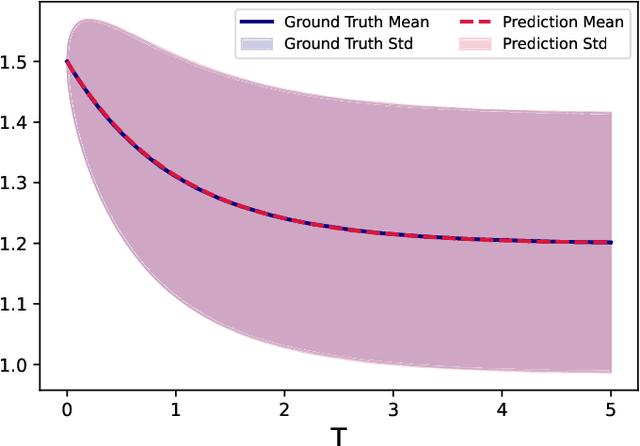
We present a numerical method to learn an accurate predictive model for an unknown stochastic dynamical system from its trajectory data. The method seeks to approximate the unknown flow map of the underlying system. It employs the idea of autoencoder to identify the unobserved latent random variables. In our approach, we design an encoding function to discover the latent variables, which are modeled as unit Gaussian, and a decoding function to reconstruct the future states of the system. Both the encoder and decoder are expressed as deep neural networks (DNNs). Once the DNNs are trained by the trajectory data, the decoder serves as a predictive model for the unknown stochastic system. Through an extensive set of numerical examples, we demonstrate that the method is able to produce long-term system predictions by using short bursts of trajectory data. It is also applicable to systems driven by non-Gaussian noises.

Flow Map Learning for Unknown Dynamical Systems: Overview, Implementation, and Benchmarks

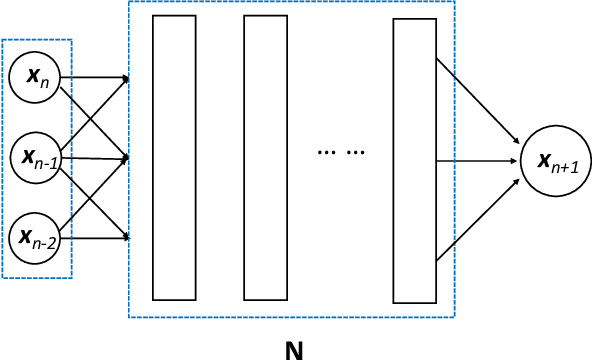
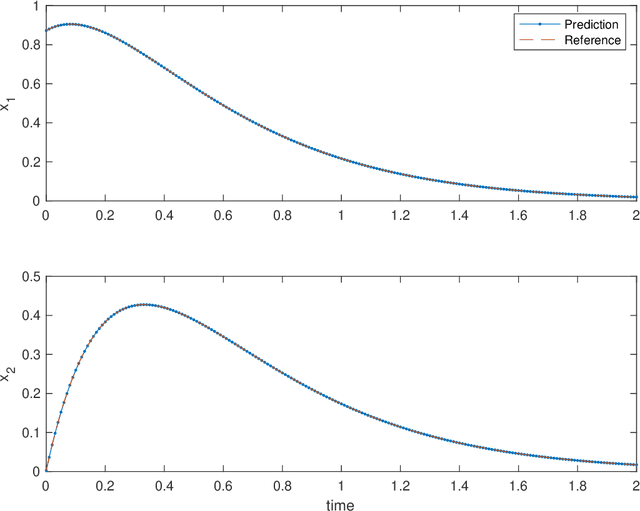
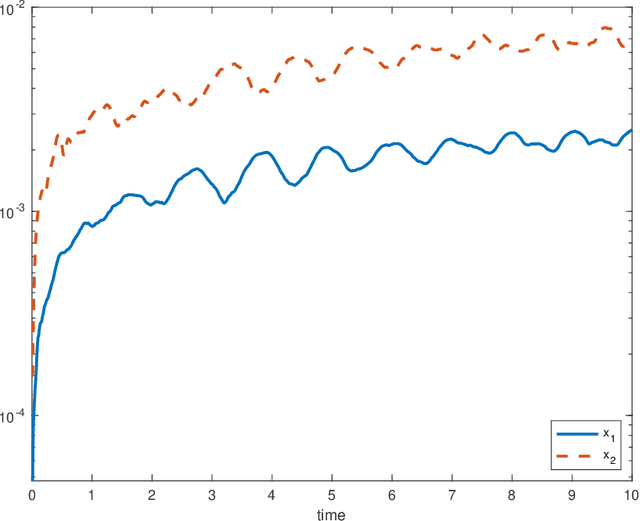
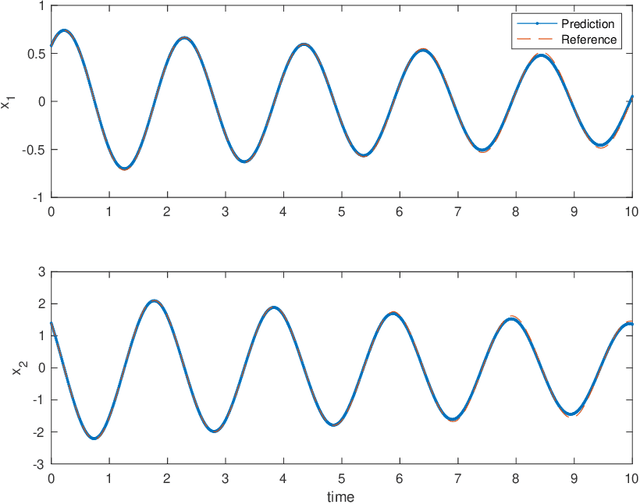
Flow map learning (FML), in conjunction with deep neural networks (DNNs), has shown promises for data driven modeling of unknown dynamical systems. A remarkable feature of FML is that it is capable of producing accurate predictive models for partially observed systems, even when their exact mathematical models do not exist. In this paper, we present an overview of the FML framework, along with the important computational details for its successful implementation. We also present a set of well defined benchmark problems for learning unknown dynamical systems. All the numerical details of these problems are presented, along with their FML results, to ensure that the problems are accessible for cross-examination and the results are reproducible.

Learning Stochastic Dynamical System via Flow Map Operator

We present a numerical framework for learning unknown stochastic dynamical systems using measurement data. Termed stochastic flow map learning (sFML), the new framework is an extension of flow map learning (FML) that was developed for learning deterministic dynamical systems. For learning stochastic systems, we define a stochastic flow map that is a superposition of two sub-flow maps: a deterministic sub-map and a stochastic sub-map. The stochastic training data are used to construct the deterministic sub-map first, followed by the stochastic sub-map. The deterministic sub-map takes the form of residual network (ResNet), similar to the work of FML for deterministic systems. For the stochastic sub-map, we employ a generative model, particularly generative adversarial networks (GANs) in this paper. The final constructed stochastic flow map then defines a stochastic evolution model that is a weak approximation, in term of distribution, of the unknown stochastic system. A comprehensive set of numerical examples are presented to demonstrate the flexibility and effectiveness of the proposed sFML method for various types of stochastic systems.