Positional Knowledge is All You Need: Position-induced Transformer for Operator Learning

Operator learning for Partial Differential Equations (PDEs) is rapidly emerging as a promising approach for surrogate modeling of intricate systems. Transformers with the self-attention mechanism$\unicode{x2013}$a powerful tool originally designed for natural language processing$\unicode{x2013}$have recently been adapted for operator learning. However, they confront challenges, including high computational demands and limited interpretability. This raises a critical question: Is there a more efficient attention mechanism for Transformer-based operator learning? This paper proposes the Position-induced Transformer (PiT), built on an innovative position-attention mechanism, which demonstrates significant advantages over the classical self-attention in operator learning. Position-attention draws inspiration from numerical methods for PDEs. Different from self-attention, position-attention is induced by only the spatial interrelations of sampling positions for input functions of the operators, and does not rely on the input function values themselves, thereby greatly boosting efficiency. PiT exhibits superior performance over current state-of-the-art neural operators in a variety of complex operator learning tasks across diverse PDE benchmarks. Additionally, PiT possesses an enhanced discretization convergence feature, compared to the widely-used Fourier neural operator.

Critical Sampling for Robust Evolution Operator Learning of Unknown Dynamical Systems

Given an unknown dynamical system, what is the minimum number of samples needed for effective learning of its governing laws and accurate prediction of its future evolution behavior, and how to select these critical samples? In this work, we propose to explore this problem based on a design approach. Starting from a small initial set of samples, we adaptively discover critical samples to achieve increasingly accurate learning of the system evolution. One central challenge here is that we do not know the network modeling error since the ground-truth system state is unknown, which is however needed for critical sampling. To address this challenge, we introduce a multi-step reciprocal prediction network where forward and backward evolution networks are designed to learn the temporal evolution behavior in the forward and backward time directions, respectively. Very interestingly, we find that the desired network modeling error is highly correlated with the multi-step reciprocal prediction error, which can be directly computed from the current system state. This allows us to perform a dynamic selection of critical samples from regions with high network modeling errors for dynamical systems. Additionally, a joint spatial-temporal evolution network is introduced which incorporates spatial dynamics modeling into the temporal evolution prediction for robust learning of the system evolution operator with few samples. Our extensive experimental results demonstrate that our proposed method is able to dramatically reduce the number of samples needed for effective learning and accurate prediction of evolution behaviors of unknown dynamical systems by up to hundreds of times.

Deep-OSG: A deep learning approach for approximating a family of operators in semigroup to model unknown autonomous systems

This paper proposes a novel deep learning approach for approximating evolution operators and modeling unknown autonomous dynamical systems using time series data collected at varied time lags. It is a sequel to the previous works [T. Qin, K. Wu, and D. Xiu, J. Comput. Phys., 395:620--635, 2019], [K. Wu and D. Xiu, J. Comput. Phys., 408:109307, 2020], and [Z. Chen, V. Churchill, K. Wu, and D. Xiu, J. Comput. Phys., 449:110782, 2022], which focused on learning single evolution operator with a fixed time step. This paper aims to learn a family of evolution operators with variable time steps, which constitute a semigroup for an autonomous system. The semigroup property is very crucial and links the system's evolutionary behaviors across varying time scales, but it was not considered in the previous works. We propose for the first time a framework of embedding the semigroup property into the data-driven learning process, through a novel neural network architecture and new loss functions. The framework is very feasible, can be combined with any suitable neural networks, and is applicable to learning general autonomous ODEs and PDEs. We present the rigorous error estimates and variance analysis to understand the prediction accuracy and robustness of our approach, showing the remarkable advantages of semigroup awareness in our model. Moreover, our approach allows one to arbitrarily choose the time steps for prediction and ensures that the predicted results are well self-matched and consistent. Extensive numerical experiments demonstrate that embedding the semigroup property notably reduces the data dependency of deep learning models and greatly improves the accuracy, robustness, and stability for long-time prediction.

Deep Neural Network Modeling of Unknown Partial Differential Equations in Nodal Space

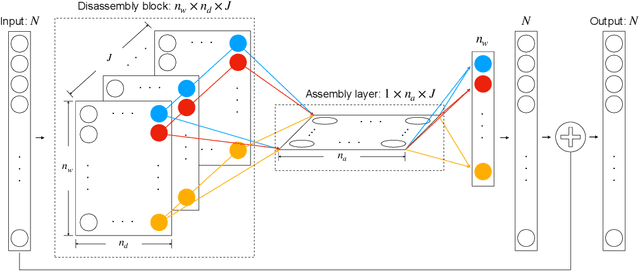
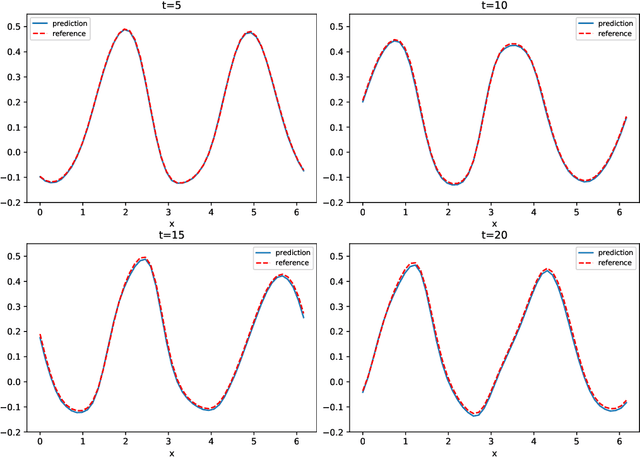
We present a numerical framework for deep neural network (DNN) modeling of unknown time-dependent partial differential equations (PDE) using their trajectory data. Unlike the recent work of [Wu and Xiu, J. Comput. Phys. 2020], where the learning takes place in modal/Fourier space, the current method conducts the learning and modeling in physical space and uses measurement data as nodal values. We present a DNN structure that has a direct correspondence to the evolution operator of the underlying PDE, thus establishing the existence of the DNN model. The DNN model also does not require any geometric information of the data nodes. Consequently, a trained DNN defines a predictive model for the underlying unknown PDE over structureless grids. A set of examples, including linear and nonlinear scalar PDE, system of PDEs, in both one dimension and two dimensions, over structured and unstructured grids, are presented to demonstrate the effectiveness of the proposed DNN modeling. Extension to other equations such as differential-integral equations is also discussed.

Methods to Recover Unknown Processes in Partial Differential Equations Using Data

We study the problem of identifying unknown processes embedded in time-dependent partial differential equation (PDE) using observational data, with an application to advection-diffusion type PDE. We first conduct theoretical analysis and derive conditions to ensure the solvability of the problem. We then present a set of numerical approaches, including Galerkin type algorithm and collocation type algorithm. Analysis of the algorithms are presented, along with their implementation detail. The Galerkin algorithm is more suitable for practical situations, particularly those with noisy data, as it avoids using derivative/gradient data. Various numerical examples are then presented to demonstrate the performance and properties of the numerical methods.

A Non-Intrusive Correction Algorithm for Classification Problems with Corrupted Data

A novel correction algorithm is proposed for multi-class classification problems with corrupted training data. The algorithm is non-intrusive, in the sense that it post-processes a trained classification model by adding a correction procedure to the model prediction. The correction procedure can be coupled with any approximators, such as logistic regression, neural networks of various architectures, etc. When training dataset is sufficiently large, we prove that the corrected models deliver correct classification results as if there is no corruption in the training data. For datasets of finite size, the corrected models produce significantly better recovery results, compared to the models without the correction algorithm. All of the theoretical findings in the paper are verified by our numerical examples.

Data-Driven Deep Learning of Partial Differential Equations in Modal Space

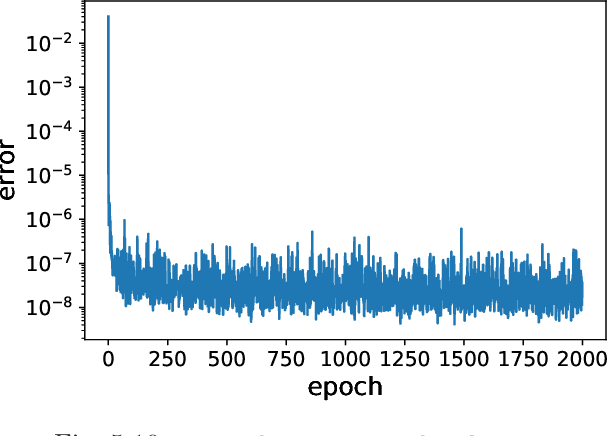
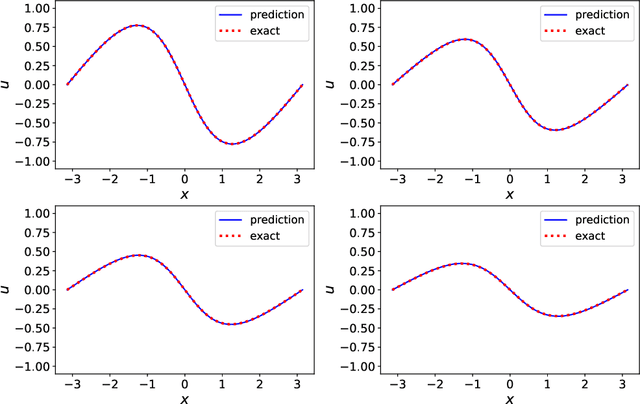
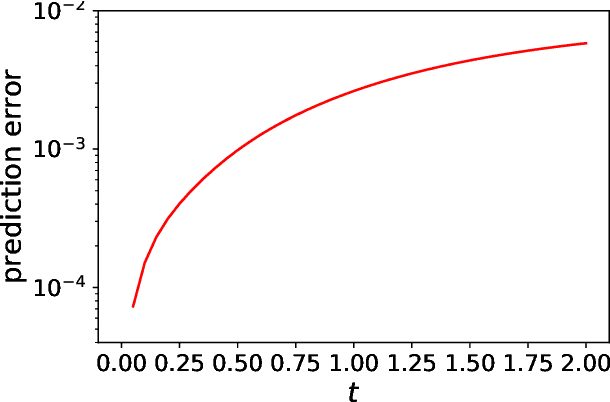
We present a framework for recovering/approximating unknown time-dependent partial differential equation (PDE) using its solution data. Instead of identifying the terms in the underlying PDE, we seek to approximate the evolution operator of the underlying PDE numerically. The evolution operator of the PDE, defined in infinite-dimensional space, maps the solution from a current time to a future time and completely characterizes the solution evolution of the underlying unknown PDE. Our recovery strategy relies on approximation of the evolution operator in a properly defined modal space, i.e., generalized Fourier space, in order to reduce the problem to finite dimensions. The finite dimensional approximation is then accomplished by training a deep neural network structure, which is based on residual network (ResNet), using the given data. Error analysis is provided to illustrate the predictive accuracy of the proposed method. A set of examples of different types of PDEs, including inviscid Burgers' equation that develops discontinuity in its solution, are presented to demonstrate the effectiveness of the proposed method.

Structure-preserving Method for Reconstructing Unknown Hamiltonian Systems from Trajectory Data

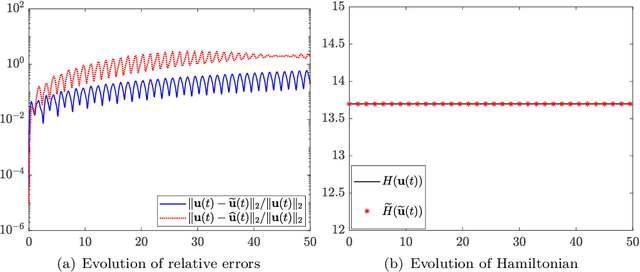
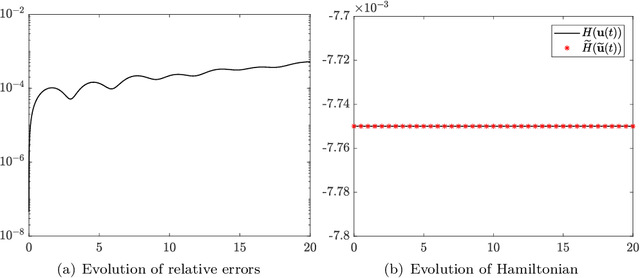
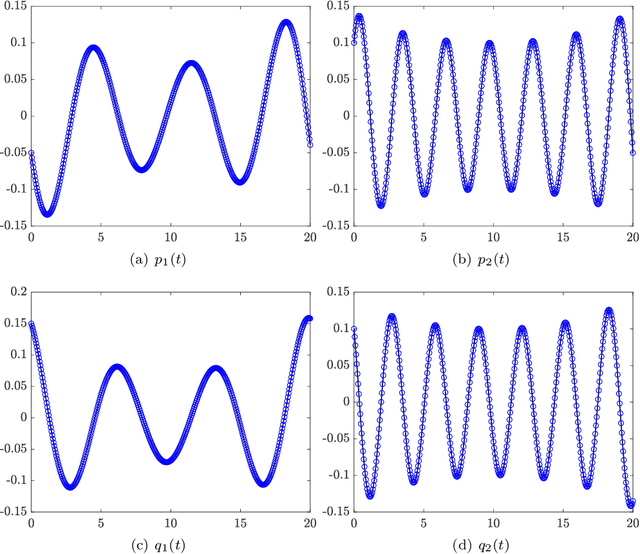
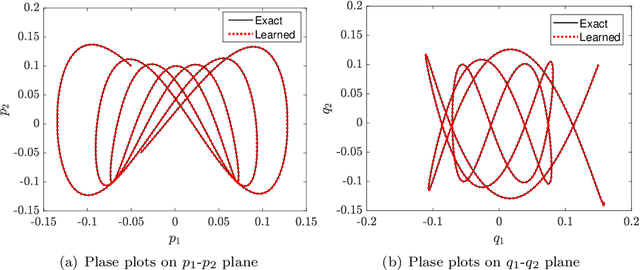
We present a numerical approach for approximating unknown Hamiltonian systems using observation data. A distinct feature of the proposed method is that it is structure-preserving, in the sense that it enforces conservation of the reconstructed Hamiltonian. This is achieved by directly approximating the underlying unknown Hamiltonian, rather than the right-hand-side of the governing equations. We present the technical details of the proposed algorithm and its error estimate, along with a practical de-noising procedure to cope with noisy data. A set of numerical examples are then presented to demonstrate the structure-preserving property and effectiveness of the algorithm.

Data Driven Governing Equations Approximation Using Deep Neural Networks

We present a numerical framework for approximating unknown governing equations using observation data and deep neural networks (DNN). In particular, we propose to use residual network (ResNet) as the basic building block for equation approximation. We demonstrate that the ResNet block can be considered as a one-step method that is exact in temporal integration. We then present two multi-step methods, recurrent ResNet (RT-ResNet) method and recursive ReNet (RS-ResNet) method. The RT-ResNet is a multi-step method on uniform time steps, whereas the RS-ResNet is an adaptive multi-step method using variable time steps. All three methods presented here are based on integral form of the underlying dynamical system. As a result, they do not require time derivative data for equation recovery and can cope with relatively coarsely distributed trajectory data. Several numerical examples are presented to demonstrate the performance of the methods.

Numerical Aspects for Approximating Governing Equations Using Data

We present effective numerical algorithms for locally recovering unknown governing differential equations from measurement data. We employ a set of standard basis functions, e.g., polynomials, to approximate the governing equation with high accuracy. Upon recasting the problem into a function approximation problem, we discuss several important aspects for accurate approximation. Most notably, we discuss the importance of using a large number of short bursts of trajectory data, rather than using data from a single long trajectory. Several options for the numerical algorithms to perform accurate approximation are then presented, along with an error estimate of the final equation approximation. We then present an extensive set of numerical examples of both linear and nonlinear systems to demonstrate the properties and effectiveness of our equation recovery algorithms.