Structure-preserving Method for Reconstructing Unknown Hamiltonian Systems from Trajectory Data
Paper and Code
May 24, 2019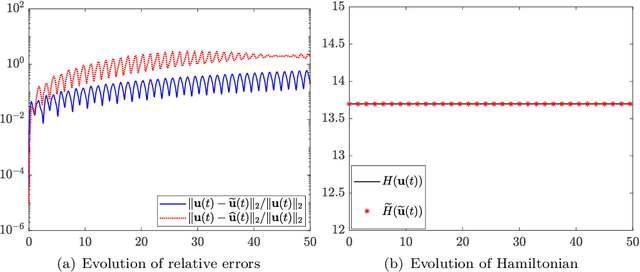
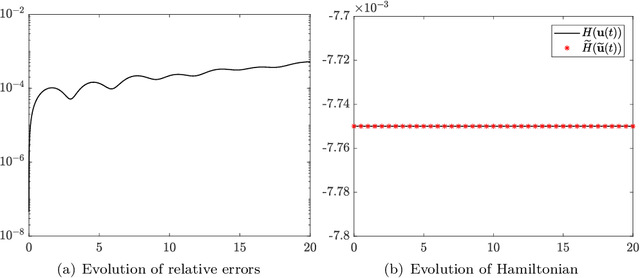
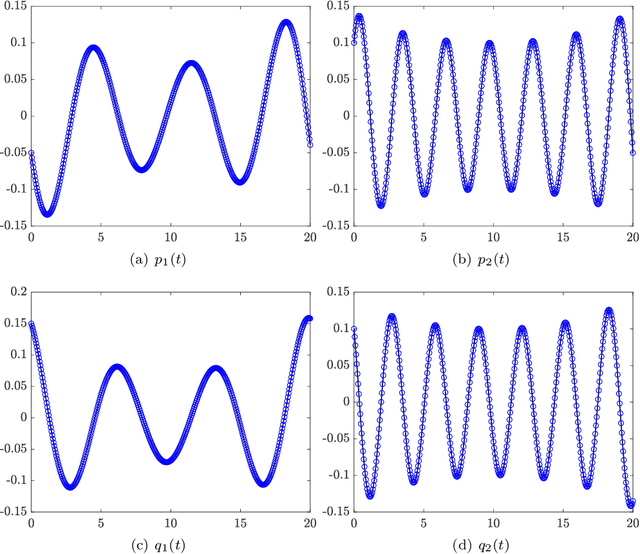
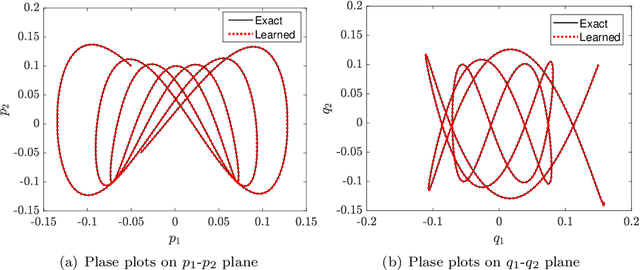
We present a numerical approach for approximating unknown Hamiltonian systems using observation data. A distinct feature of the proposed method is that it is structure-preserving, in the sense that it enforces conservation of the reconstructed Hamiltonian. This is achieved by directly approximating the underlying unknown Hamiltonian, rather than the right-hand-side of the governing equations. We present the technical details of the proposed algorithm and its error estimate, along with a practical de-noising procedure to cope with noisy data. A set of numerical examples are then presented to demonstrate the structure-preserving property and effectiveness of the algorithm.
* 24 pages, 16 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge