Deep Neural Network Modeling of Unknown Partial Differential Equations in Nodal Space
Paper and Code
Jun 07, 2021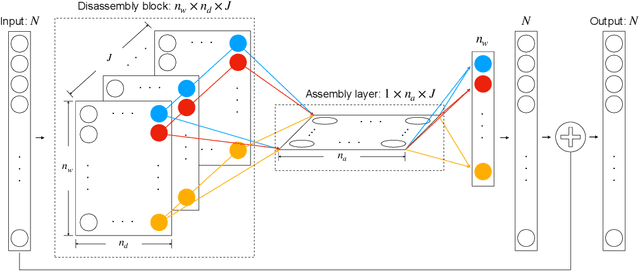

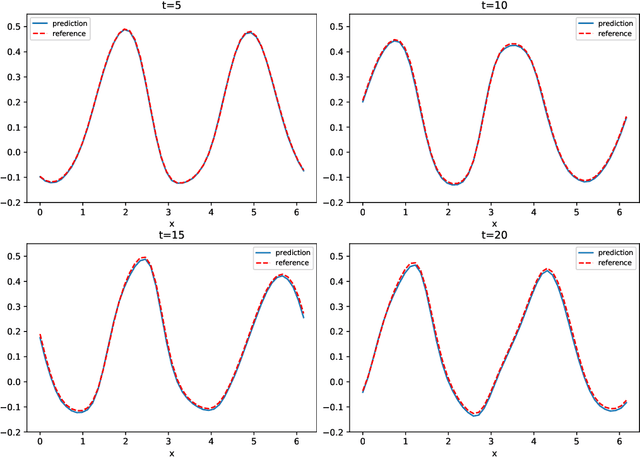

We present a numerical framework for deep neural network (DNN) modeling of unknown time-dependent partial differential equations (PDE) using their trajectory data. Unlike the recent work of [Wu and Xiu, J. Comput. Phys. 2020], where the learning takes place in modal/Fourier space, the current method conducts the learning and modeling in physical space and uses measurement data as nodal values. We present a DNN structure that has a direct correspondence to the evolution operator of the underlying PDE, thus establishing the existence of the DNN model. The DNN model also does not require any geometric information of the data nodes. Consequently, a trained DNN defines a predictive model for the underlying unknown PDE over structureless grids. A set of examples, including linear and nonlinear scalar PDE, system of PDEs, in both one dimension and two dimensions, over structured and unstructured grids, are presented to demonstrate the effectiveness of the proposed DNN modeling. Extension to other equations such as differential-integral equations is also discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge