Principal Component Flow Map Learning of PDEs from Incomplete, Limited, and Noisy Data

We present a computational technique for modeling the evolution of dynamical systems in a reduced basis, with a focus on the challenging problem of modeling partially-observed partial differential equations (PDEs) on high-dimensional non-uniform grids. We address limitations of previous work on data-driven flow map learning in the sense that we focus on noisy and limited data to move toward data collection scenarios in real-world applications. Leveraging recent work on modeling PDEs in modal and nodal spaces, we present a neural network structure that is suitable for PDE modeling with noisy and limited data available only on a subset of the state variables or computational domain. In particular, spatial grid-point measurements are reduced using a learned linear transformation, after which the dynamics are learned in this reduced basis before being transformed back out to the nodal space. This approach yields a drastically reduced parameterization of the neural network compared with previous flow map models for nodal space learning. This primarily allows for smaller training data sets, but also enables reduced training times.

Flow Map Learning for Unknown Dynamical Systems: Overview, Implementation, and Benchmarks

Flow map learning (FML), in conjunction with deep neural networks (DNNs), has shown promises for data driven modeling of unknown dynamical systems. A remarkable feature of FML is that it is capable of producing accurate predictive models for partially observed systems, even when their exact mathematical models do not exist. In this paper, we present an overview of the FML framework, along with the important computational details for its successful implementation. We also present a set of well defined benchmark problems for learning unknown dynamical systems. All the numerical details of these problems are presented, along with their FML results, to ensure that the problems are accessible for cross-examination and the results are reproducible.

Sub-aperture SAR Imaging with Uncertainty Quantification

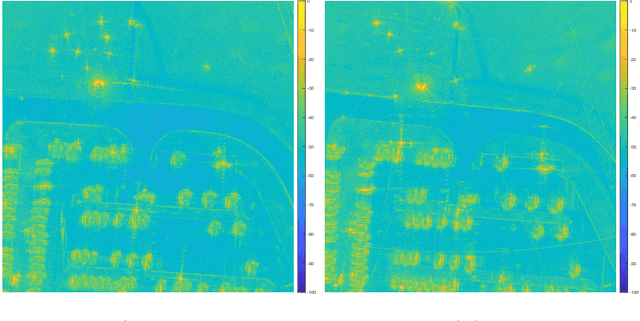
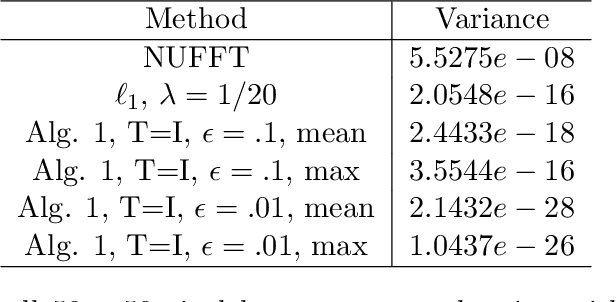
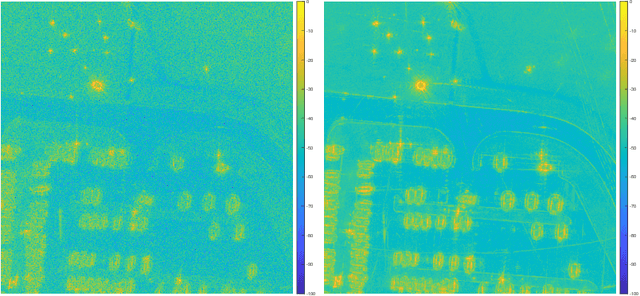
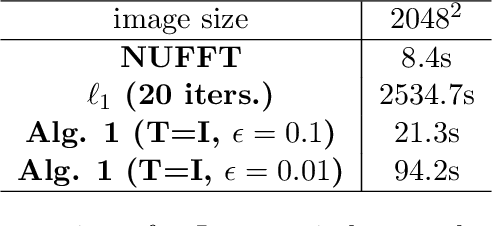
In the problem of spotlight mode airborne synthetic aperture radar (SAR) image formation, it is well-known that data collected over a wide azimuthal angle violate the isotropic scattering property typically assumed. Many techniques have been proposed to account for this issue, including both full-aperture and sub-aperture methods based on filtering, regularized least squares, and Bayesian methods. A full-aperture method that uses a hierarchical Bayesian prior to incorporate appropriate speckle modeling and reduction was recently introduced to produce samples of the posterior density rather than a single image estimate. This uncertainty quantification information is more robust as it can generate a variety of statistics for the scene. As proposed, the method was not well-suited for large problems, however, as the sampling was inefficient. Moreover, the method was not explicitly designed to mitigate the effects of the faulty isotropic scattering assumption. In this work we therefore propose a new sub-aperture SAR imaging method that uses a sparse Bayesian learning-type algorithm to more efficiently produce approximate posterior densities for each sub-aperture window. These estimates may be useful in and of themselves, or when of interest, the statistics from these distributions can be combined to form a composite image. Furthermore, unlike the often-employed lp-regularized least squares methods, no user-defined parameters are required. Application-specific adjustments are made to reduce the typically burdensome runtime and storage requirements so that appropriately large images can be generated. Finally, this paper focuses on incorporating these techniques into SAR image formation process. That is, for the problem starting with SAR phase history data, so that no additional processing errors are incurred.

Learning Fine Scale Dynamics from Coarse Observations via Inner Recurrence

Recent work has focused on data-driven learning of the evolution of unknown systems via deep neural networks (DNNs), with the goal of conducting long term prediction of the dynamics of the unknown system. In many real-world applications, data from time-dependent systems are often collected on a time scale that is coarser than desired, due to various restrictions during the data acquisition process. Consequently, the observed dynamics can be severely under-sampled and do not reflect the true dynamics of the underlying system. This paper presents a computational technique to learn the fine-scale dynamics from such coarsely observed data. The method employs inner recurrence of a DNN to recover the fine-scale evolution operator of the underlying system. In addition to mathematical justification, several challenging numerical examples, including unknown systems of both ordinary and partial differential equations, are presented to demonstrate the effectiveness of the proposed method.

Deep Learning of Chaotic Systems from Partially-Observed Data

Recently, a general data driven numerical framework has been developed for learning and modeling of unknown dynamical systems using fully- or partially-observed data. The method utilizes deep neural networks (DNNs) to construct a model for the flow map of the unknown system. Once an accurate DNN approximation of the flow map is constructed, it can be recursively executed to serve as an effective predictive model of the unknown system. In this paper, we apply this framework to chaotic systems, in particular the well-known Lorenz 63 and 96 systems, and critically examine the predictive performance of the approach. A distinct feature of chaotic systems is that even the smallest perturbations will lead to large (albeit bounded) deviations in the solution trajectories. This makes long-term predictions of the method, or any data driven methods, questionable, as the local model accuracy will eventually degrade and lead to large pointwise errors. Here we employ several other qualitative and quantitative measures to determine whether the chaotic dynamics have been learned. These include phase plots, histograms, autocorrelation, correlation dimension, approximate entropy, and Lyapunov exponent. Using these measures, we demonstrate that the flow map based DNN learning method is capable of accurately modeling chaotic systems, even when only a subset of the state variables are available to the DNNs. For example, for the Lorenz 96 system with 40 state variables, when data of only 3 variables are available, the method is able to learn an effective DNN model for the 3 variables and produce accurately the chaotic behavior of the system.

Robust Modeling of Unknown Dynamical Systems via Ensemble Averaged Learning

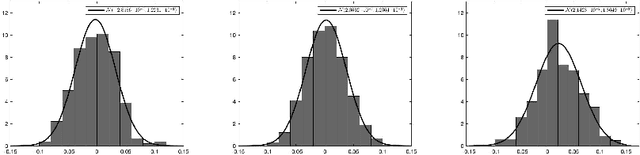
Recent work has focused on data-driven learning of the evolution of unknown systems via deep neural networks (DNNs), with the goal of conducting long time prediction of the evolution of the unknown system. Training a DNN with low generalization error is a particularly important task in this case as error is accumulated over time. Because of the inherent randomness in DNN training, chiefly in stochastic optimization, there is uncertainty in the resulting prediction, and therefore in the generalization error. Hence, the generalization error can be viewed as a random variable with some probability distribution. Well-trained DNNs, particularly those with many hyperparameters, typically result in probability distributions for generalization error with low bias but high variance. High variance causes variability and unpredictably in the results of a trained DNN. This paper presents a computational technique which decreases the variance of the generalization error, thereby improving the reliability of the DNN model to generalize consistently. In the proposed ensemble averaging method, multiple models are independently trained and model predictions are averaged at each time step. A mathematical foundation for the method is presented, including results regarding the distribution of the local truncation error. In addition, three time-dependent differential equation problems are considered as numerical examples, demonstrating the effectiveness of the method to decrease variance of DNN predictions generally.

Deep Neural Network Modeling of Unknown Partial Differential Equations in Nodal Space

We present a numerical framework for deep neural network (DNN) modeling of unknown time-dependent partial differential equations (PDE) using their trajectory data. Unlike the recent work of [Wu and Xiu, J. Comput. Phys. 2020], where the learning takes place in modal/Fourier space, the current method conducts the learning and modeling in physical space and uses measurement data as nodal values. We present a DNN structure that has a direct correspondence to the evolution operator of the underlying PDE, thus establishing the existence of the DNN model. The DNN model also does not require any geometric information of the data nodes. Consequently, a trained DNN defines a predictive model for the underlying unknown PDE over structureless grids. A set of examples, including linear and nonlinear scalar PDE, system of PDEs, in both one dimension and two dimensions, over structured and unstructured grids, are presented to demonstrate the effectiveness of the proposed DNN modeling. Extension to other equations such as differential-integral equations is also discussed.