A Training-Free Conditional Diffusion Model for Learning Stochastic Dynamical Systems

This study introduces a training-free conditional diffusion model for learning unknown stochastic differential equations (SDEs) using data. The proposed approach addresses key challenges in computational efficiency and accuracy for modeling SDEs by utilizing a score-based diffusion model to approximate their stochastic flow map. Unlike the existing methods, this technique is based on an analytically derived closed-form exact score function, which can be efficiently estimated by Monte Carlo method using the trajectory data, and eliminates the need for neural network training to learn the score function. By generating labeled data through solving the corresponding reverse ordinary differential equation, the approach enables supervised learning of the flow map. Extensive numerical experiments across various SDE types, including linear, nonlinear, and multi-dimensional systems, demonstrate the versatility and effectiveness of the method. The learned models exhibit significant improvements in predicting both short-term and long-term behaviors of unknown stochastic systems, often surpassing baseline methods like GANs in estimating drift and diffusion coefficients.

LERENet: Eliminating Intra-class Differences for Metal Surface Defect Few-shot Semantic Segmentation

Few-shot segmentation models excel in metal defect detection due to their rapid generalization ability to new classes and pixel-level segmentation, rendering them ideal for addressing data scarcity issues and achieving refined object delineation in industrial applications. Existing works neglect the \textit{Intra-Class Differences}, inherent in metal surface defect data, which hinders the model from learning sufficient knowledge from the support set to guide the query set segmentation. Specifically, it can be categorized into two types: the \textit{Semantic Difference} induced by internal factors in metal samples and the \textit{Distortion Difference} caused by external factors of surroundings. To address these differences, we introduce a \textbf{L}ocal d\textbf{E}scriptor based \textbf{R}easoning and \textbf{E}xcitation \textbf{Net}work (\textbf{LERENet}) to learn the two-view guidance, i.e., local and global information from the graph and feature space, and fuse them to segment precisely. Since the relation structure of local features embedded in graph space will help to eliminate \textit{Semantic Difference}, we employ Multi-Prototype Reasoning (MPR) module, extracting local descriptors based prototypes and analyzing local-view feature relevance in support-query pairs. Besides, due to the global information that will assist in countering the \textit{Distortion Difference} in observations, we utilize Multi-Prototype Excitation (MPE) module to capture the global-view relations in support-query pairs. Finally, we employ an Information Fusion Module (IFM) to fuse learned prototypes in local and global views to generate pixel-level masks. Our comprehensive experiments on defect datasets demonstrate that it outperforms existing benchmarks, establishing a new state-of-the-art.

Deep Bayesian Reinforcement Learning for Spacecraft Proximity Maneuvers and Docking

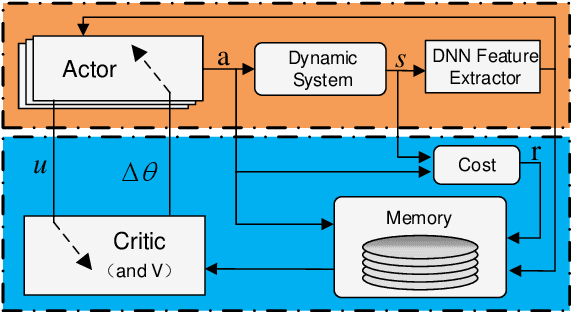
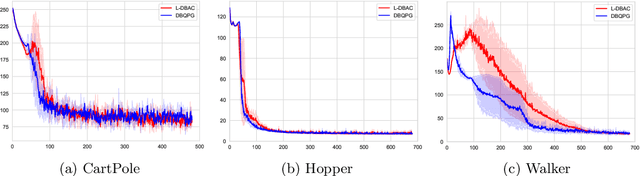
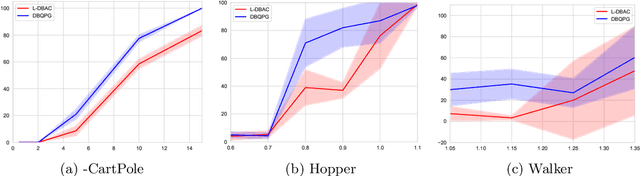
In the pursuit of autonomous spacecraft proximity maneuvers and docking(PMD), we introduce a novel Bayesian actor-critic reinforcement learning algorithm to learn a control policy with the stability guarantee. The PMD task is formulated as a Markov decision process that reflects the relative dynamic model, the docking cone and the cost function. Drawing from the principles of Lyapunov theory, we frame the temporal difference learning as a constrained Gaussian process regression problem. This innovative approach allows the state-value function to be expressed as a Lyapunov function, leveraging the Gaussian process and deep kernel learning. We develop a novel Bayesian quadrature policy optimization procedure to analytically compute the policy gradient while integrating Lyapunov-based stability constraints. This integration is pivotal in satisfying the rigorous safety demands of spaceflight missions. The proposed algorithm has been experimentally evaluated on a spacecraft air-bearing testbed and shows impressive and promising performance.

Diffusion-Model-Assisted Supervised Learning of Generative Models for Density Estimation

We present a supervised learning framework of training generative models for density estimation. Generative models, including generative adversarial networks, normalizing flows, variational auto-encoders, are usually considered as unsupervised learning models, because labeled data are usually unavailable for training. Despite the success of the generative models, there are several issues with the unsupervised training, e.g., requirement of reversible architectures, vanishing gradients, and training instability. To enable supervised learning in generative models, we utilize the score-based diffusion model to generate labeled data. Unlike existing diffusion models that train neural networks to learn the score function, we develop a training-free score estimation method. This approach uses mini-batch-based Monte Carlo estimators to directly approximate the score function at any spatial-temporal location in solving an ordinary differential equation (ODE), corresponding to the reverse-time stochastic differential equation (SDE). This approach can offer both high accuracy and substantial time savings in neural network training. Once the labeled data are generated, we can train a simple fully connected neural network to learn the generative model in the supervised manner. Compared with existing normalizing flow models, our method does not require to use reversible neural networks and avoids the computation of the Jacobian matrix. Compared with existing diffusion models, our method does not need to solve the reverse-time SDE to generate new samples. As a result, the sampling efficiency is significantly improved. We demonstrate the performance of our method by applying it to a set of 2D datasets as well as real data from the UCI repository.

Contrastive Prompt Learning-based Code Search based on Interaction Matrix

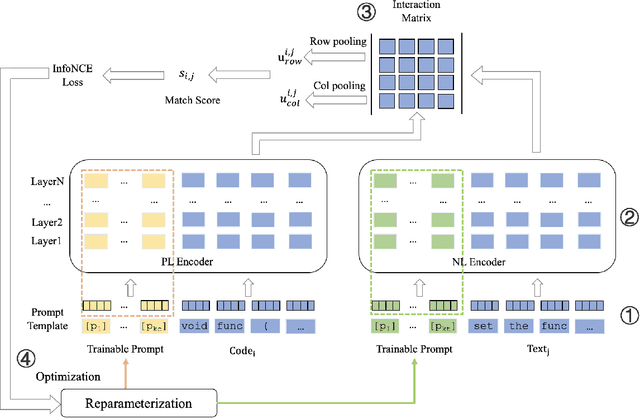
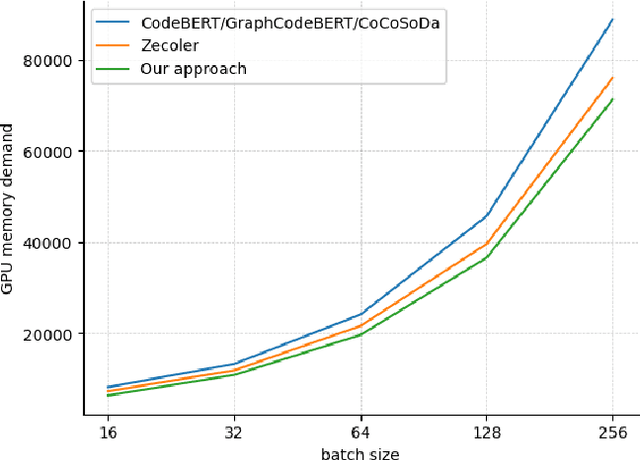
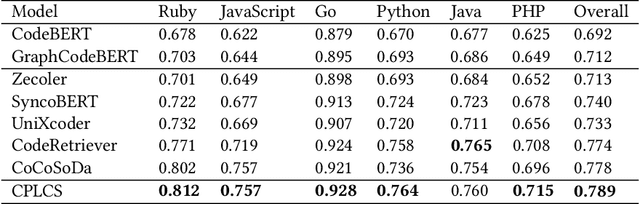
Code search aims to retrieve the code snippet that highly matches the given query described in natural language. Recently, many code pre-training approaches have demonstrated impressive performance on code search. However, existing code search methods still suffer from two performance constraints: inadequate semantic representation and the semantic gap between natural language (NL) and programming language (PL). In this paper, we propose CPLCS, a contrastive prompt learning-based code search method based on the cross-modal interaction mechanism. CPLCS comprises:(1) PL-NL contrastive learning, which learns the semantic matching relationship between PL and NL representations; (2) a prompt learning design for a dual-encoder structure that can alleviate the problem of inadequate semantic representation; (3) a cross-modal interaction mechanism to enhance the fine-grained mapping between NL and PL. We conduct extensive experiments to evaluate the effectiveness of our approach on a real-world dataset across six programming languages. The experiment results demonstrate the efficacy of our approach in improving semantic representation quality and mapping ability between PL and NL.

Seeking the Yield Barrier: High-Dimensional SRAM Evaluation Through Optimal Manifold

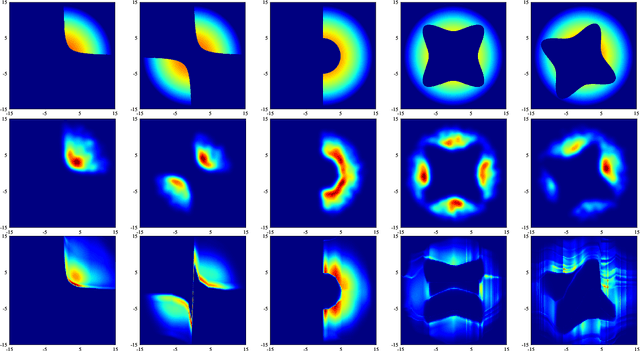
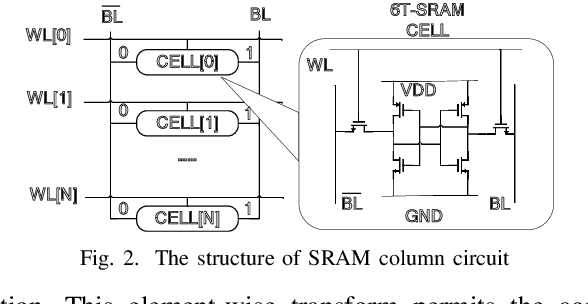
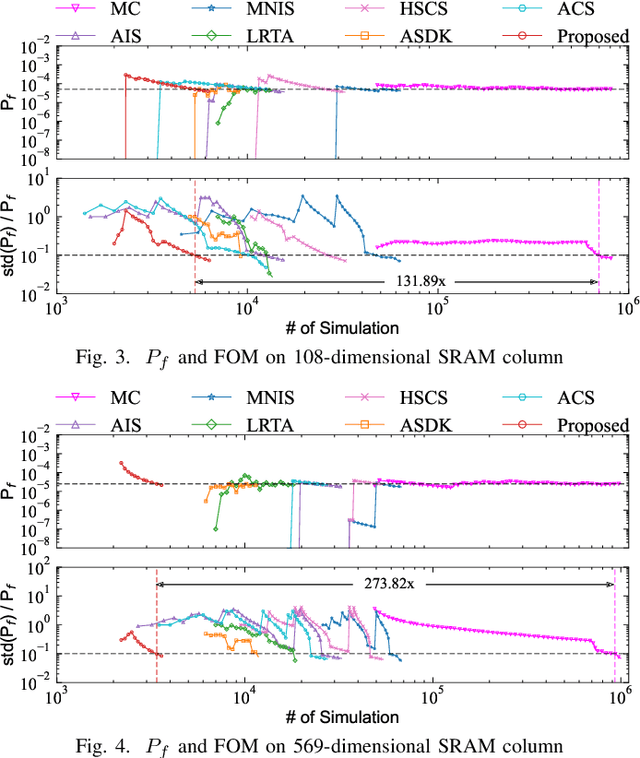
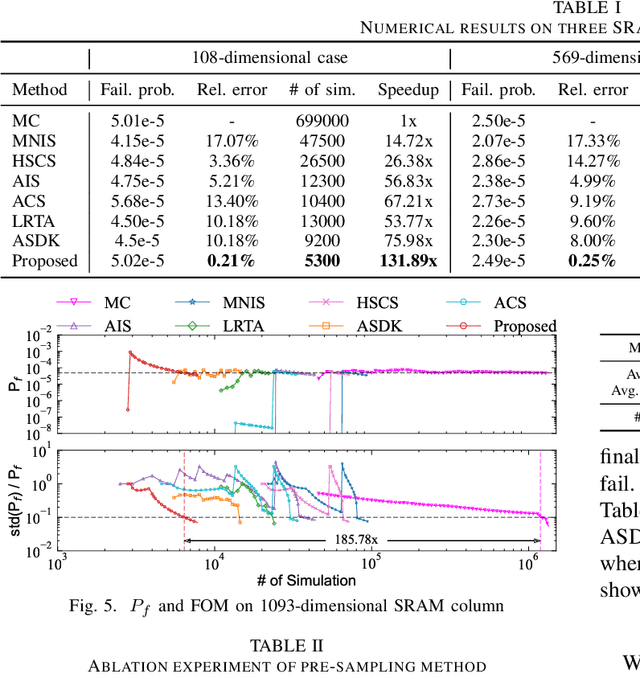
Being able to efficiently obtain an accurate estimate of the failure probability of SRAM components has become a central issue as model circuits shrink their scale to submicrometer with advanced technology nodes. In this work, we revisit the classic norm minimization method. We then generalize it with infinite components and derive the novel optimal manifold concept, which bridges the surrogate-based and importance sampling (IS) yield estimation methods. We then derive a sub-optimal manifold, optimal hypersphere, which leads to an efficient sampling method being aware of the failure boundary called onion sampling. Finally, we use a neural coupling flow (which learns from samples like a surrogate model) as the IS proposal distribution. These combinations give rise to a novel yield estimation method, named Optimal Manifold Important Sampling (OPTIMIS), which keeps the advantages of the surrogate and IS methods to deliver state-of-the-art performance with robustness and consistency, with up to 3.5x in efficiency and 3x in accuracy over the best of SOTA methods in High-dimensional SRAM evaluation.

Covering matroid

In this paper, we propose a new type of matroids, namely covering matroids, and investigate the connections with the second type of covering-based rough sets and some existing special matroids. Firstly, as an extension of partitions, coverings are more natural combinatorial objects and can sometimes be more efficient to deal with problems in the real world. Through extending partitions to coverings, we propose a new type of matroids called covering matroids and prove them to be an extension of partition matroids. Secondly, since some researchers have successfully applied partition matroids to classical rough sets, we study the relationships between covering matroids and covering-based rough sets which are an extension of classical rough sets. Thirdly, in matroid theory, there are many special matroids, such as transversal matroids, partition matroids, 2-circuit matroid and partition-circuit matroids. The relationships among several special matroids and covering matroids are studied.

Relation matroid and its relationship with generalized rough set based on relation

Recently, the relationship between matroids and generalized rough sets based on relations has been studied from the viewpoint of linear independence of matrices. In this paper, we reveal more relationships by the predecessor and successor neighborhoods from relations. First, through these two neighborhoods, we propose a pair of matroids, namely predecessor relation matroid and successor relation matroid, respectively. Basic characteristics of this pair of matroids, such as dependent sets, circuits, the rank function and the closure operator, are described by the predecessor and successor neighborhoods from relations. Second, we induce a relation from a matroid through the circuits of the matroid. We prove that the induced relation is always an equivalence relation. With these two inductions, a relation induces a relation matroid, and the relation matroid induces an equivalence relation, then the connection between the original relation and the induced equivalence relation is studied. Moreover, the relationships between the upper approximation operator in generalized rough sets and the closure operator in matroids are investigated.

Matroidal structure of rough sets based on serial and transitive relations

The theory of rough sets is concerned with the lower and upper approximations of objects through a binary relation on a universe. It has been applied to machine learning, knowledge discovery and data mining. The theory of matroids is a generalization of linear independence in vector spaces. It has been used in combinatorial optimization and algorithm design. In order to take advantages of both rough sets and matroids, in this paper we propose a matroidal structure of rough sets based on a serial and transitive relation on a universe. We define the family of all minimal neighborhoods of a relation on a universe, and prove it satisfy the circuit axioms of matroids when the relation is serial and transitive. In order to further study this matroidal structure, we investigate the inverse of this construction: inducing a relation by a matroid. The relationships between the upper approximation operators of rough sets based on relations and the closure operators of matroids in the above two constructions are studied. Moreover, we investigate the connections between the above two constructions.

Characteristic of partition-circuit matroid through approximation number

Rough set theory is a useful tool to deal with uncertain, granular and incomplete knowledge in information systems. And it is based on equivalence relations or partitions. Matroid theory is a structure that generalizes linear independence in vector spaces, and has a variety of applications in many fields. In this paper, we propose a new type of matroids, namely, partition-circuit matroids, which are induced by partitions. Firstly, a partition satisfies circuit axioms in matroid theory, then it can induce a matroid which is called a partition-circuit matroid. A partition and an equivalence relation on the same universe are one-to-one corresponding, then some characteristics of partition-circuit matroids are studied through rough sets. Secondly, similar to the upper approximation number which is proposed by Wang and Zhu, we define the lower approximation number. Some characteristics of partition-circuit matroids and the dual matroids of them are investigated through the lower approximation number and the upper approximation number.