Hybrid Channel Based Pedestrian Detection

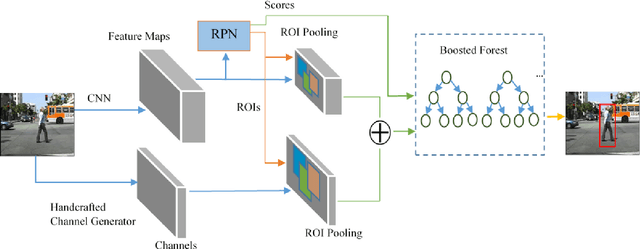
Pedestrian detection has achieved great improvements with the help of Convolutional Neural Networks (CNNs). CNN can learn high-level features from input images, but the insufficient spatial resolution of CNN feature channels (feature maps) may cause a loss of information, which is harmful especially to small instances. In this paper, we propose a new pedestrian detection framework, which extends the successful RPN+BF framework to combine handcrafted features and CNN features. RoI-pooling is used to extract features from both handcrafted channels (e.g. HOG+LUV, CheckerBoards or RotatedFilters) and CNN channels. Since handcrafted channels always have higher spatial resolution than CNN channels, we apply RoI-pooling with larger output resolution to handcrafted channels to keep more detailed information. Our ablation experiments show that the developed handcrafted features can reach better detection accuracy than the CNN features extracted from the VGG-16 net, and a performance gain can be achieved by combining them. Experimental results on Caltech pedestrian dataset with the original annotations and the improved annotations demonstrate the effectiveness of the proposed approach. When using a more advanced RPN in our framework, our approach can be further improved and get competitive results on both benchmarks.

Dependence space of matroids and its application to attribute reduction

Attribute reduction is a basic issue in knowledge representation and data mining. Rough sets provide a theoretical foundation for the issue. Matroids generalized from matrices have been widely used in many fields, particularly greedy algorithm design, which plays an important role in attribute reduction. Therefore, it is meaningful to combine matroids with rough sets to solve the optimization problems. In this paper, we introduce an existing algebraic structure called dependence space to study the reduction problem in terms of matroids. First, a dependence space of matroids is constructed. Second, the characterizations for the space such as consistent sets and reducts are studied through matroids. Finally, we investigate matroids by the means of the space and present two expressions for their bases. In a word, this paper provides new approaches to study attribute reduction.

Connectedness of graphs and its application to connected matroids through covering-based rough sets

Graph theoretical ideas are highly utilized by computer science fields especially data mining. In this field, a data structure can be designed in the form of tree. Covering is a widely used form of data representation in data mining and covering-based rough sets provide a systematic approach to this type of representation. In this paper, we study the connectedness of graphs through covering-based rough sets and apply it to connected matroids. First, we present an approach to inducing a covering by a graph, and then study the connectedness of the graph from the viewpoint of the covering approximation operators. Second, we construct a graph from a matroid, and find the matroid and the graph have the same connectedness, which makes us to use covering-based rough sets to study connected matroids. In summary, this paper provides a new approach to studying graph theory and matroid theory.

Geometric lattice structure of covering and its application to attribute reduction through matroids

The reduction of covering decision systems is an important problem in data mining, and covering-based rough sets serve as an efficient technique to process the problem. Geometric lattices have been widely used in many fields, especially greedy algorithm design which plays an important role in the reduction problems. Therefore, it is meaningful to combine coverings with geometric lattices to solve the optimization problems. In this paper, we obtain geometric lattices from coverings through matroids and then apply them to the issue of attribute reduction. First, a geometric lattice structure of a covering is constructed through transversal matroids. Then its atoms are studied and used to describe the lattice. Second, considering that all the closed sets of a finite matroid form a geometric lattice, we propose a dependence space through matroids and study the attribute reduction issues of the space, which realizes the application of geometric lattices to attribute reduction. Furthermore, a special type of information system is taken as an example to illustrate the application. In a word, this work points out an interesting view, namely, geometric lattice to study the attribute reduction issues of information systems.

Closed-set lattice of regular sets based on a serial and transitive relation through matroids

Rough sets are efficient for data pre-processing in data mining. Matroids are based on linear algebra and graph theory, and have a variety of applications in many fields. Both rough sets and matroids are closely related to lattices. For a serial and transitive relation on a universe, the collection of all the regular sets of the generalized rough set is a lattice. In this paper, we use the lattice to construct a matroid and then study relationships between the lattice and the closed-set lattice of the matroid. First, the collection of all the regular sets based on a serial and transitive relation is proved to be a semimodular lattice. Then, a matroid is constructed through the height function of the semimodular lattice. Finally, we propose an approach to obtain all the closed sets of the matroid from the semimodular lattice. Borrowing from matroids, results show that lattice theory provides an interesting view to investigate rough sets.

Connectivity for matroids based on rough sets

In mathematics and computer science, connectivity is one of the basic concepts of matroid theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems. The connectivity of a matroid is an important measure of its robustness as a network. Therefore, it is very necessary to investigate the conditions under which a matroid is connected. In this paper, the connectivity for matroids is studied through relation-based rough sets. First, a symmetric and transitive relation is introduced from a general matroid and its properties are explored from the viewpoint of matroids. Moreover, through the relation introduced by a general matroid, an undirected graph is generalized. Specifically, the connection of the graph can be investigated by the relation-based rough sets. Second, we study the connectivity for matroids by means of relation-based rough sets and some conditions under which a general matroid is connected are presented. Finally, it is easy to prove that the connectivity for a general matroid with some special properties and its induced undirected graph is equivalent. These results show an important application of relation-based rough sets to matroids.

Rough matroids based on coverings

The introduction of covering-based rough sets has made a substantial contribution to the classical rough sets. However, many vital problems in rough sets, including attribution reduction, are NP-hard and therefore the algorithms for solving them are usually greedy. Matroid, as a generalization of linear independence in vector spaces, it has a variety of applications in many fields such as algorithm design and combinatorial optimization. An excellent introduction to the topic of rough matroids is due to Zhu and Wang. On the basis of their work, we study the rough matroids based on coverings in this paper. First, we investigate some properties of the definable sets with respect to a covering. Specifically, it is interesting that the set of all definable sets with respect to a covering, equipped with the binary relation of inclusion $\subseteq$, constructs a lattice. Second, we propose the rough matroids based on coverings, which are a generalization of the rough matroids based on relations. Finally, some properties of rough matroids based on coverings are explored. Moreover, an equivalent formulation of rough matroids based on coverings is presented. These interesting and important results exhibit many potential connections between rough sets and matroids.

A necessary and sufficient condition for two relations to induce the same definable set family

In Pawlak rough sets, the structure of the definable set families is simple and clear, but in generalizing rough sets, the structure of the definable set families is a bit more complex. There has been much research work focusing on this topic. However, as a fundamental issue in relation based rough sets, under what condition two relations induce the same definable set family has not been discussed. In this paper, based on the concept of the closure of relations, we present a necessary and sufficient condition for two relations to induce the same definable set family.

Applications of repeat degree on coverings of neighborhoods

In covering based rough sets, the neighborhood of an element is the intersection of all the covering blocks containing the element. All the neighborhoods form a new covering called a covering of neighborhoods. In the course of studying under what condition a covering of neighborhoods is a partition, the concept of repeat degree is proposed, with the help of which the issue is addressed. This paper studies further the application of repeat degree on coverings of neighborhoods. First, we investigate under what condition a covering of neighborhoods is the reduct of the covering inducing it. As a preparation for addressing this issue, we give a necessary and sufficient condition for a subset of a set family to be the reduct of the set family. Then we study under what condition two coverings induce a same relation and a same covering of neighborhoods. Finally, we give the method of calculating the covering according to repeat degree.

Test-cost-sensitive attribute reduction of data with normal distribution measurement errors

The measurement error with normal distribution is universal in applications. Generally, smaller measurement error requires better instrument and higher test cost. In decision making based on attribute values of objects, we shall select an attribute subset with appropriate measurement error to minimize the total test cost. Recently, error-range-based covering rough set with uniform distribution error was proposed to investigate this issue. However, the measurement errors satisfy normal distribution instead of uniform distribution which is rather simple for most applications. In this paper, we introduce normal distribution measurement errors to covering-based rough set model, and deal with test-cost-sensitive attribute reduction problem in this new model. The major contributions of this paper are four-fold. First, we build a new data model based on normal distribution measurement errors. With the new data model, the error range is an ellipse in a two-dimension space. Second, the covering-based rough set with normal distribution measurement errors is constructed through the "3-sigma" rule. Third, the test-cost-sensitive attribute reduction problem is redefined on this covering-based rough set. Fourth, a heuristic algorithm is proposed to deal with this problem. The algorithm is tested on ten UCI (University of California - Irvine) datasets. The experimental results show that the algorithm is more effective and efficient than the existing one. This study is a step toward realistic applications of cost-sensitive learning.