Jiyan Zhang
LERENet: Eliminating Intra-class Differences for Metal Surface Defect Few-shot Semantic Segmentation
Mar 17, 2024Abstract:Few-shot segmentation models excel in metal defect detection due to their rapid generalization ability to new classes and pixel-level segmentation, rendering them ideal for addressing data scarcity issues and achieving refined object delineation in industrial applications. Existing works neglect the \textit{Intra-Class Differences}, inherent in metal surface defect data, which hinders the model from learning sufficient knowledge from the support set to guide the query set segmentation. Specifically, it can be categorized into two types: the \textit{Semantic Difference} induced by internal factors in metal samples and the \textit{Distortion Difference} caused by external factors of surroundings. To address these differences, we introduce a \textbf{L}ocal d\textbf{E}scriptor based \textbf{R}easoning and \textbf{E}xcitation \textbf{Net}work (\textbf{LERENet}) to learn the two-view guidance, i.e., local and global information from the graph and feature space, and fuse them to segment precisely. Since the relation structure of local features embedded in graph space will help to eliminate \textit{Semantic Difference}, we employ Multi-Prototype Reasoning (MPR) module, extracting local descriptors based prototypes and analyzing local-view feature relevance in support-query pairs. Besides, due to the global information that will assist in countering the \textit{Distortion Difference} in observations, we utilize Multi-Prototype Excitation (MPE) module to capture the global-view relations in support-query pairs. Finally, we employ an Information Fusion Module (IFM) to fuse learned prototypes in local and global views to generate pixel-level masks. Our comprehensive experiments on defect datasets demonstrate that it outperforms existing benchmarks, establishing a new state-of-the-art.
The APC Algorithm of Solving Large-Scale Linear Systems: A Generalized Analysis
Sep 16, 2022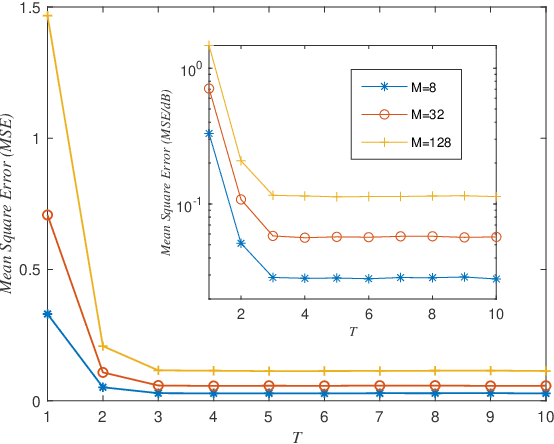
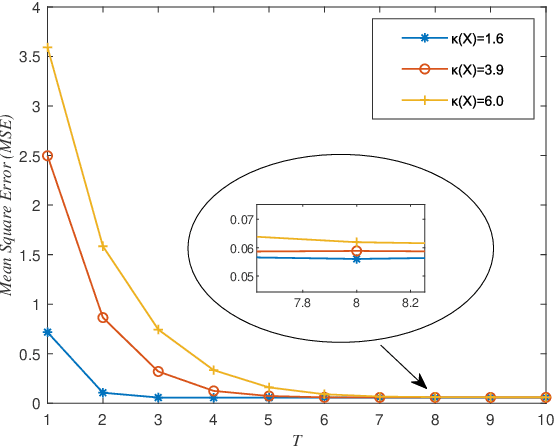
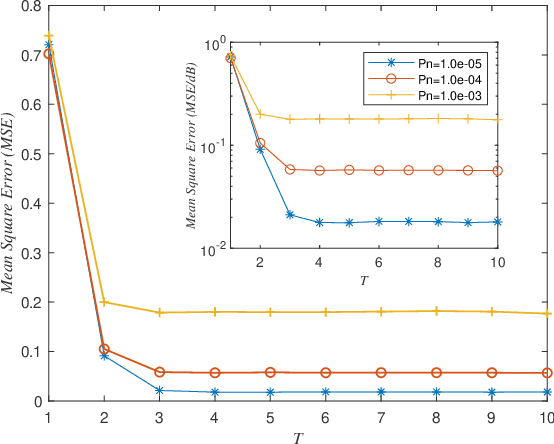
Abstract:A new algorithm called accelerated projection-based consensus (APC) has recently emerged as a promising approach to solve large-scale systems of linear equations in a distributed fashion. The algorithm adopts the federated architecture, and attracts increasing research interest; however, it's performance analysis is still incomplete, e.g., the error performance under noisy condition has not yet been investigated. In this paper, we focus on providing a generalized analysis by the use of the linear system theory, such that the error performance of the APC algorithm for solving linear systems in presence of additive noise can be clarified. We specifically provide a closed-form expression of the error of solution attained by the APC algorithm. Numerical results demonstrate the error performance of the APC algorithm, validating the presented analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge