Monte Carlo Diffusion for Generalizable Learning-Based RANSAC

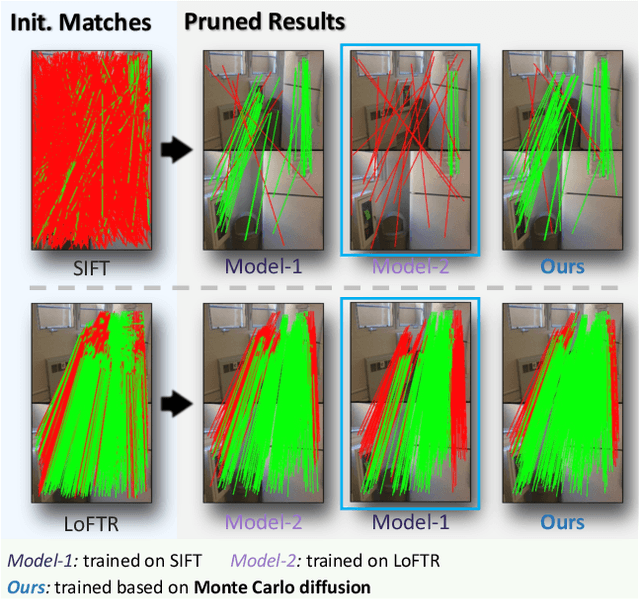
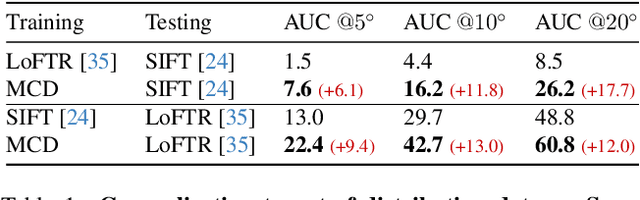
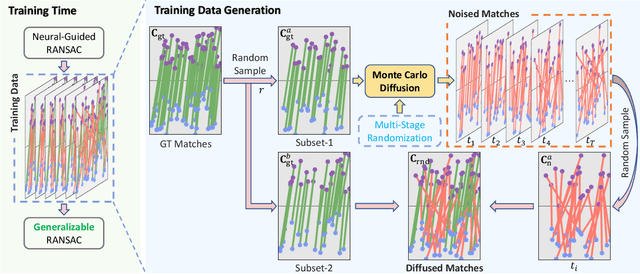
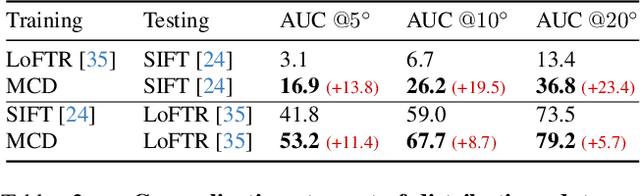
Random Sample Consensus (RANSAC) is a fundamental approach for robustly estimating parametric models from noisy data. Existing learning-based RANSAC methods utilize deep learning to enhance the robustness of RANSAC against outliers. However, these approaches are trained and tested on the data generated by the same algorithms, leading to limited generalization to out-of-distribution data during inference. Therefore, in this paper, we introduce a novel diffusion-based paradigm that progressively injects noise into ground-truth data, simulating the noisy conditions for training learning-based RANSAC. To enhance data diversity, we incorporate Monte Carlo sampling into the diffusion paradigm, approximating diverse data distributions by introducing different types of randomness at multiple stages. We evaluate our approach in the context of feature matching through comprehensive experiments on the ScanNet and MegaDepth datasets. The experimental results demonstrate that our Monte Carlo diffusion mechanism significantly improves the generalization ability of learning-based RANSAC. We also develop extensive ablation studies that highlight the effectiveness of key components in our framework.

Enhancing Complex Formula Recognition with Hierarchical Detail-Focused Network

Hierarchical and complex Mathematical Expression Recognition (MER) is challenging due to multiple possible interpretations of a formula, complicating both parsing and evaluation. In this paper, we introduce the Hierarchical Detail-Focused Recognition dataset (HDR), the first dataset specifically designed to address these issues. It consists of a large-scale training set, HDR-100M, offering an unprecedented scale and diversity with one hundred million training instances. And the test set, HDR-Test, includes multiple interpretations of complex hierarchical formulas for comprehensive model performance evaluation. Additionally, the parsing of complex formulas often suffers from errors in fine-grained details. To address this, we propose the Hierarchical Detail-Focused Recognition Network (HDNet), an innovative framework that incorporates a hierarchical sub-formula module, focusing on the precise handling of formula details, thereby significantly enhancing MER performance. Experimental results demonstrate that HDNet outperforms existing MER models across various datasets.

F3T: A soft tactile unit with 3D force and temperature mathematical decoupling ability for robots

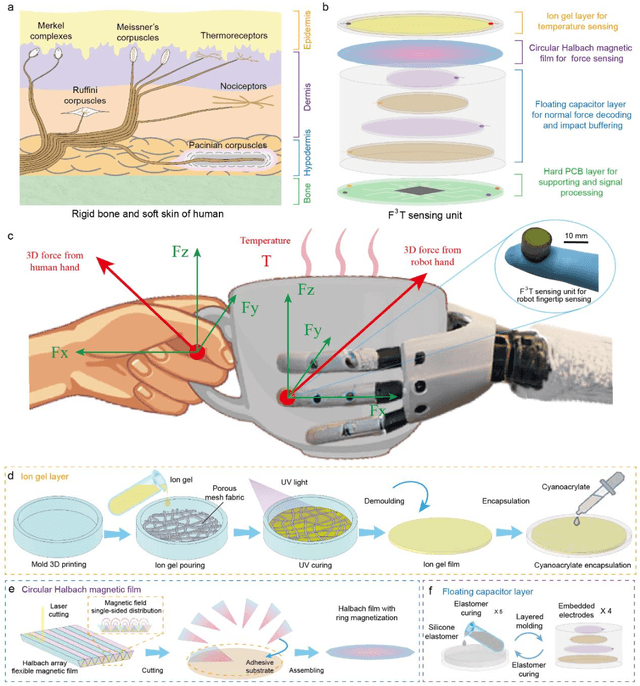
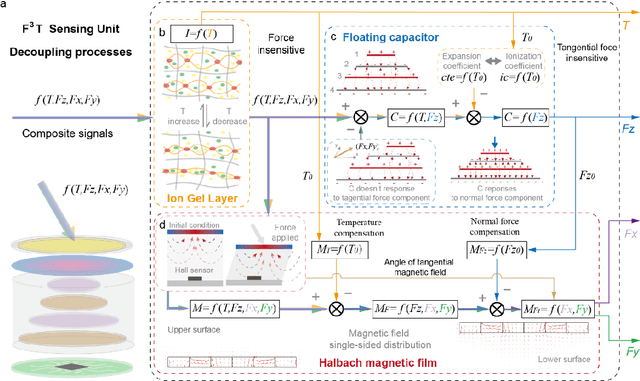
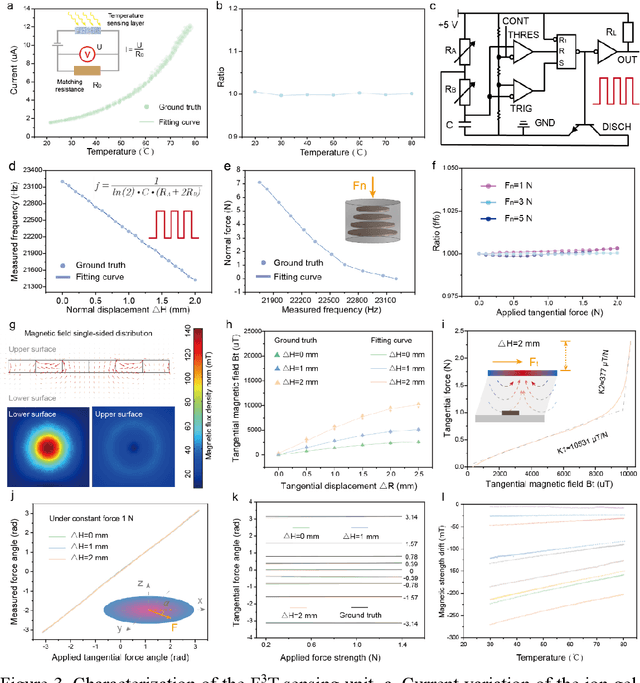
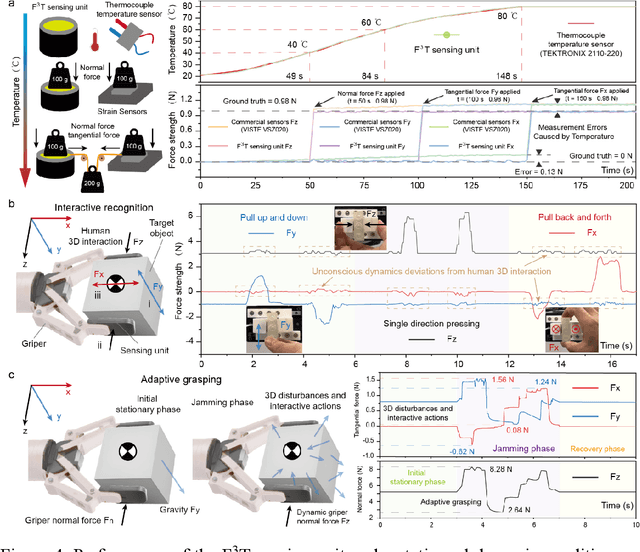
The human skin exhibits remarkable capability to perceive contact forces and environmental temperatures, providing intricate information essential for nuanced manipulation. Despite recent advancements in soft tactile sensors, a significant challenge remains in accurately decoupling signals - specifically, separating force from directional orientation and temperature - resulting in fail to meet the advanced application requirements of robots. This research proposes a multi-layered soft sensor unit (F3T) designed to achieve isolated measurements and mathematical decoupling of normal pressure, omnidirectional tangential forces, and temperature. We developed a circular coaxial magnetic film featuring a floating-mountain multi-layer capacitor, facilitating the physical decoupling of normal and tangential forces in all directions. Additionally, we incorporated an ion gel-based temperature sensing film atop the tactile sensor. This sensor is resilient to external pressure and deformation, enabling it to measure temperature and, crucially, eliminate capacitor errors induced by environmental temperature changes. This innovative design allows for the decoupled measurement of multiple signals, paving the way for advancements in higher-level robot motion control, autonomous decision-making, and task planning.

First Multi-Dimensional Evaluation of Flowchart Comprehension for Multimodal Large Language Models

With the development of Multimodal Large Language Models (MLLMs) technology, its general capabilities are increasingly powerful. To evaluate the various abilities of MLLMs, numerous evaluation systems have emerged. But now there is still a lack of a comprehensive method to evaluate MLLMs in the tasks related to flowcharts, which are very important in daily life and work. We propose the first comprehensive method, FlowCE, to assess MLLMs across various dimensions for tasks related to flowcharts. It encompasses evaluating MLLMs' abilities in Reasoning, Localization Recognition, Information Extraction, Logical Verification, and Summarization on flowcharts. However, we find that even the GPT4o model achieves only a score of 56.63. Among open-source models, Phi-3-Vision obtained the highest score of 49.97. We hope that FlowCE can contribute to future research on MLLMs for tasks based on flowcharts. \url{https://github.com/360AILAB-NLP/FlowCE} \end{abstract}

The APC Algorithm of Solving Large-Scale Linear Systems: A Generalized Analysis

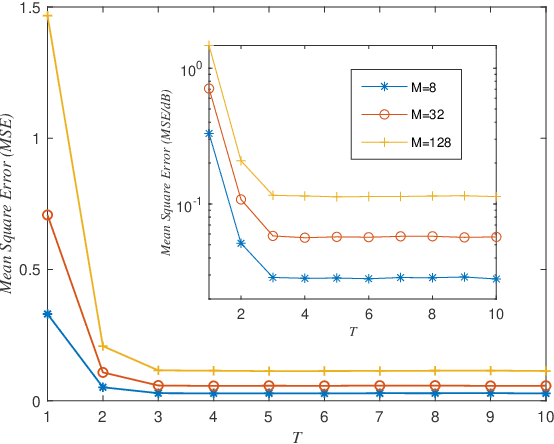
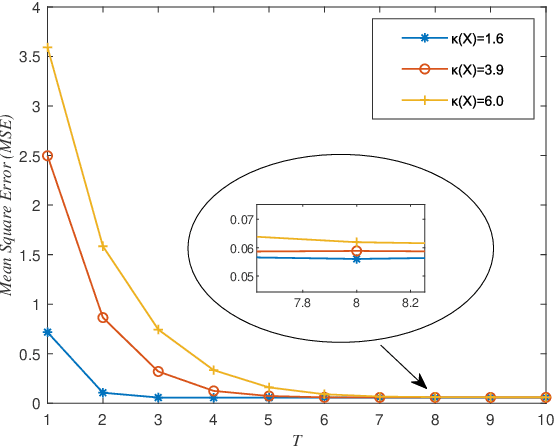
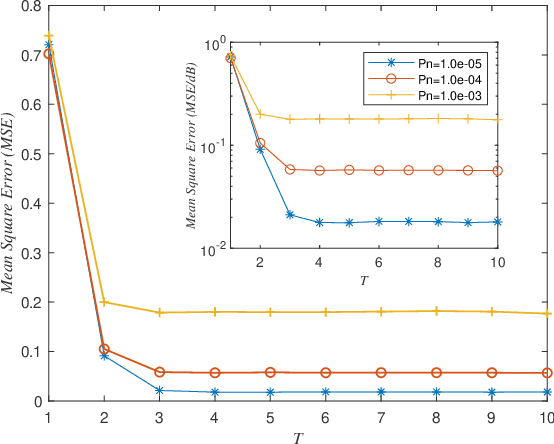
A new algorithm called accelerated projection-based consensus (APC) has recently emerged as a promising approach to solve large-scale systems of linear equations in a distributed fashion. The algorithm adopts the federated architecture, and attracts increasing research interest; however, it's performance analysis is still incomplete, e.g., the error performance under noisy condition has not yet been investigated. In this paper, we focus on providing a generalized analysis by the use of the linear system theory, such that the error performance of the APC algorithm for solving linear systems in presence of additive noise can be clarified. We specifically provide a closed-form expression of the error of solution attained by the APC algorithm. Numerical results demonstrate the error performance of the APC algorithm, validating the presented analysis.