Oksana A. Chkrebtii
Dimension-reduced Reconstruction Map Learning for Parameter Estimation in Likelihood-Free Inference Problems
Jul 19, 2024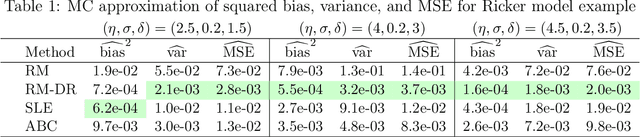
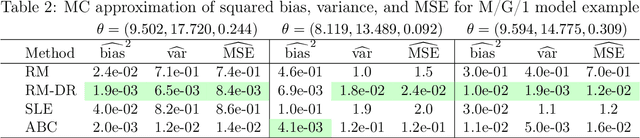
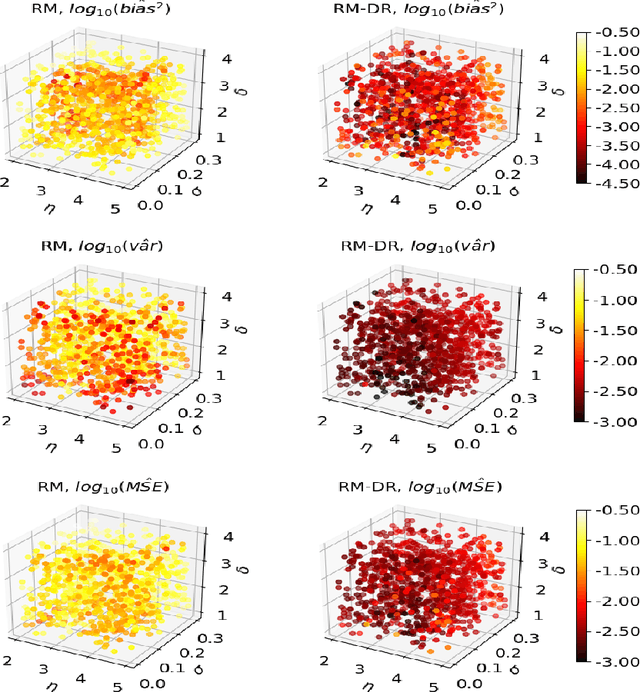
Abstract:Many application areas rely on models that can be readily simulated but lack a closed-form likelihood, or an accurate approximation under arbitrary parameter values. Existing parameter estimation approaches in this setting are generally approximate. Recent work on using neural network models to reconstruct the mapping from the data space to the parameters from a set of synthetic parameter-data pairs suffers from the curse of dimensionality, resulting in inaccurate estimation as the data size grows. We propose a dimension-reduced approach to likelihood-free estimation which combines the ideas of reconstruction map estimation with dimension-reduction approaches based on subject-specific knowledge. We examine the properties of reconstruction map estimation with and without dimension reduction and explore the trade-off between approximation error due to information loss from reducing the data dimension and approximation error. Numerical examples show that the proposed approach compares favorably with reconstruction map estimation, approximate Bayesian computation, and synthetic likelihood estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge