Spatio-temporal Multivariate Cluster Evolution Analysis for Detecting and Tracking Climate Impacts

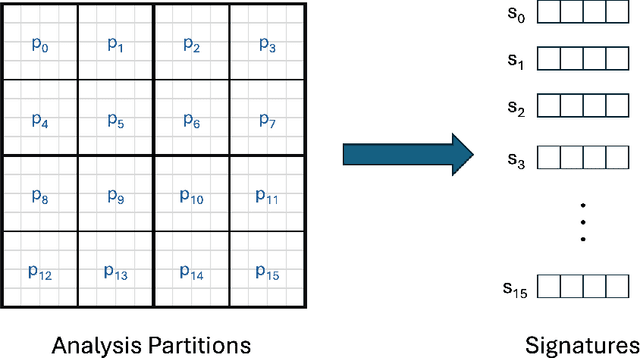
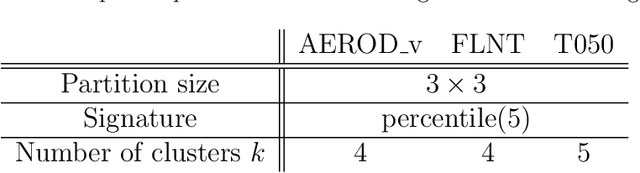
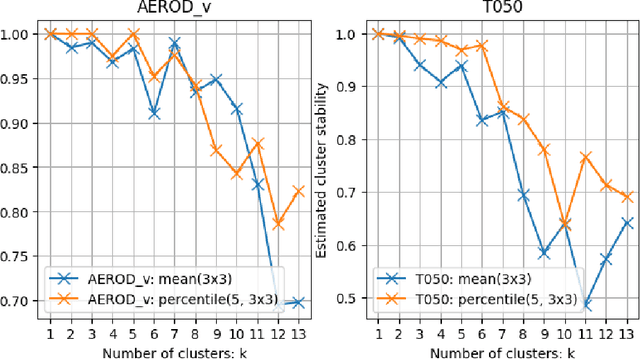
Recent years have seen a growing concern about climate change and its impacts. While Earth System Models (ESMs) can be invaluable tools for studying the impacts of climate change, the complex coupling processes encoded in ESMs and the large amounts of data produced by these models, together with the high internal variability of the Earth system, can obscure important source-to-impact relationships. This paper presents a novel and efficient unsupervised data-driven approach for detecting statistically-significant impacts and tracing spatio-temporal source-impact pathways in the climate through a unique combination of ideas from anomaly detection, clustering and Natural Language Processing (NLP). Using as an exemplar the 1991 eruption of Mount Pinatubo in the Philippines, we demonstrate that the proposed approach is capable of detecting known post-eruption impacts/events. We additionally describe a methodology for extracting meaningful sequences of post-eruption impacts/events by using NLP to efficiently mine frequent multivariate cluster evolutions, which can be used to confirm or discover the chain of physical processes between a climate source and its impact(s).

Solving High-Dimensional Inverse Problems with Auxiliary Uncertainty via Operator Learning with Limited Data

In complex large-scale systems such as climate, important effects are caused by a combination of confounding processes that are not fully observable. The identification of sources from observations of system state is vital for attribution and prediction, which inform critical policy decisions. The difficulty of these types of inverse problems lies in the inability to isolate sources and the cost of simulating computational models. Surrogate models may enable the many-query algorithms required for source identification, but data challenges arise from high dimensionality of the state and source, limited ensembles of costly model simulations to train a surrogate model, and few and potentially noisy state observations for inversion due to measurement limitations. The influence of auxiliary processes adds an additional layer of uncertainty that further confounds source identification. We introduce a framework based on (1) calibrating deep neural network surrogates to the flow maps provided by an ensemble of simulations obtained by varying sources, and (2) using these surrogates in a Bayesian framework to identify sources from observations via optimization. Focusing on an atmospheric dispersion exemplar, we find that the expressive and computationally efficient nature of the deep neural network operator surrogates in appropriately reduced dimension allows for source identification with uncertainty quantification using limited data. Introducing a variable wind field as an auxiliary process, we find that a Bayesian approximation error approach is essential for reliable source inversion when uncertainty due to wind stresses the algorithm.

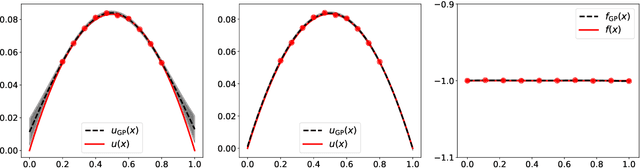
Gaussian Process Regression constrained by Boundary Value Problems

We develop a framework for Gaussian processes regression constrained by boundary value problems. The framework may be applied to infer the solution of a well-posed boundary value problem with a known second-order differential operator and boundary conditions, but for which only scattered observations of the source term are available. Scattered observations of the solution may also be used in the regression. The framework combines co-kriging with the linear transformation of a Gaussian process together with the use of kernels given by spectral expansions in eigenfunctions of the boundary value problem. Thus, it benefits from a reduced-rank property of covariance matrices. We demonstrate that the resulting framework yields more accurate and stable solution inference as compared to physics-informed Gaussian process regression without boundary condition constraints.

A Survey of Constrained Gaussian Process Regression: Approaches and Implementation Challenges

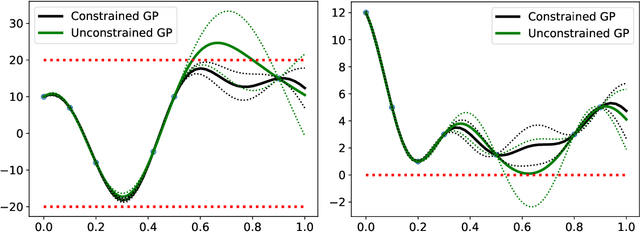
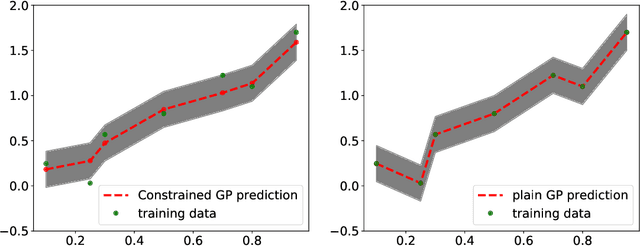
Gaussian process regression is a popular Bayesian framework for surrogate modeling of expensive data sources. As part of a broader effort in scientific machine learning, many recent works have incorporated physical constraints or other a priori information within Gaussian process regression to supplement limited data and regularize the behavior of the model. We provide an overview and survey of several classes of Gaussian process constraints, including positivity or bound constraints, monotonicity and convexity constraints, differential equation constraints provided by linear PDEs, and boundary condition constraints. We compare the strategies behind each approach as well as the differences in implementation, concluding with a discussion of the computational challenges introduced by constraints.

Tensor Basis Gaussian Process Models of Hyperelastic Materials

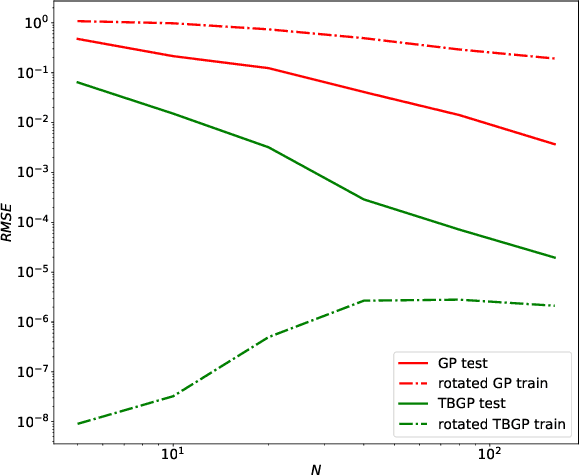
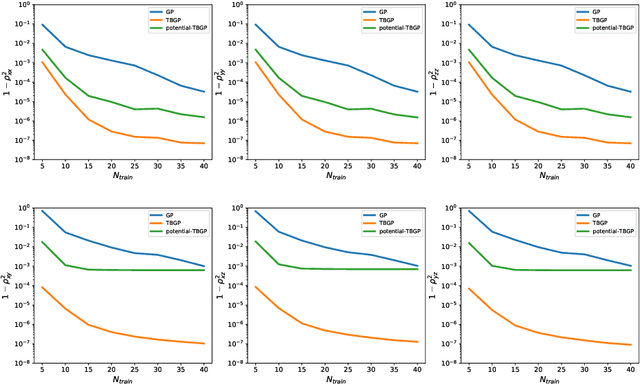
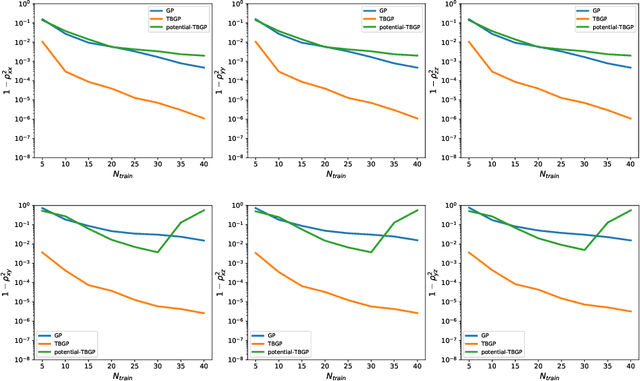
In this work, we develop Gaussian process regression (GPR) models of hyperelastic material behavior. First, we consider the direct approach of modeling the components of the Cauchy stress tensor as a function of the components of the Finger stretch tensor in a Gaussian process. We then consider an improvement on this approach that embeds rotational invariance of the stress-stretch constitutive relation in the GPR representation. This approach requires fewer training examples and achieves higher accuracy while maintaining invariance to rotations exactly. Finally, we consider an approach that recovers the strain-energy density function and derives the stress tensor from this potential. Although the error of this model for predicting the stress tensor is higher, the strain-energy density is recovered with high accuracy from limited training data. The approaches presented here are examples of physics-informed machine learning. They go beyond purely data-driven approaches by embedding the physical system constraints directly into the Gaussian process representation of materials models.