Tensor Basis Gaussian Process Models of Hyperelastic Materials
Paper and Code
Dec 23, 2019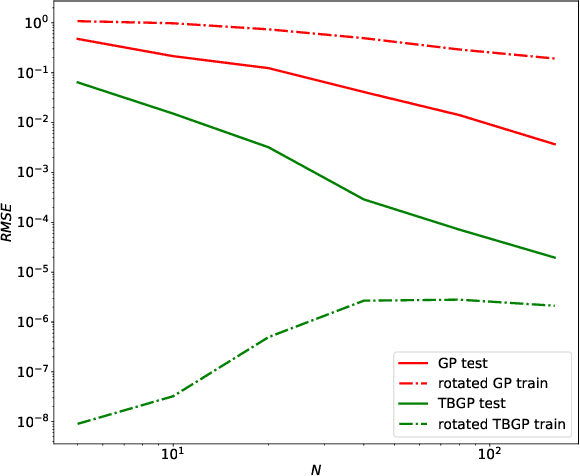

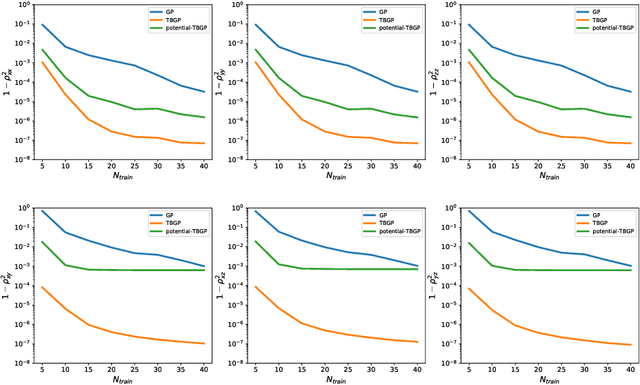
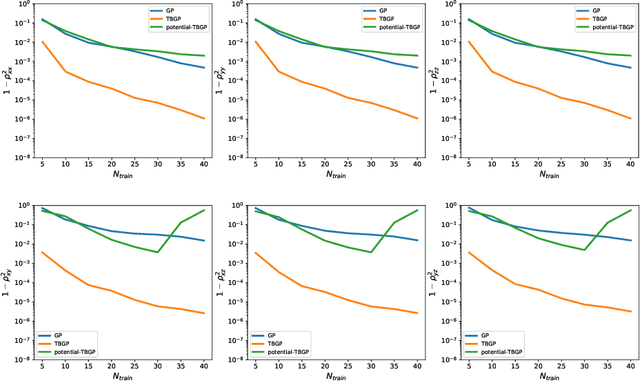
In this work, we develop Gaussian process regression (GPR) models of hyperelastic material behavior. First, we consider the direct approach of modeling the components of the Cauchy stress tensor as a function of the components of the Finger stretch tensor in a Gaussian process. We then consider an improvement on this approach that embeds rotational invariance of the stress-stretch constitutive relation in the GPR representation. This approach requires fewer training examples and achieves higher accuracy while maintaining invariance to rotations exactly. Finally, we consider an approach that recovers the strain-energy density function and derives the stress tensor from this potential. Although the error of this model for predicting the stress tensor is higher, the strain-energy density is recovered with high accuracy from limited training data. The approaches presented here are examples of physics-informed machine learning. They go beyond purely data-driven approaches by embedding the physical system constraints directly into the Gaussian process representation of materials models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge