Solving High-Dimensional Inverse Problems with Auxiliary Uncertainty via Operator Learning with Limited Data

In complex large-scale systems such as climate, important effects are caused by a combination of confounding processes that are not fully observable. The identification of sources from observations of system state is vital for attribution and prediction, which inform critical policy decisions. The difficulty of these types of inverse problems lies in the inability to isolate sources and the cost of simulating computational models. Surrogate models may enable the many-query algorithms required for source identification, but data challenges arise from high dimensionality of the state and source, limited ensembles of costly model simulations to train a surrogate model, and few and potentially noisy state observations for inversion due to measurement limitations. The influence of auxiliary processes adds an additional layer of uncertainty that further confounds source identification. We introduce a framework based on (1) calibrating deep neural network surrogates to the flow maps provided by an ensemble of simulations obtained by varying sources, and (2) using these surrogates in a Bayesian framework to identify sources from observations via optimization. Focusing on an atmospheric dispersion exemplar, we find that the expressive and computationally efficient nature of the deep neural network operator surrogates in appropriately reduced dimension allows for source identification with uncertainty quantification using limited data. Introducing a variable wind field as an auxiliary process, we find that a Bayesian approximation error approach is essential for reliable source inversion when uncertainty due to wind stresses the algorithm.

Error-in-variables modelling for operator learning

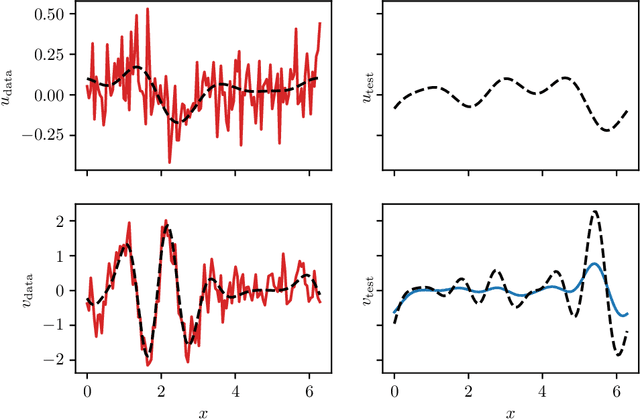
Deep operator learning has emerged as a promising tool for reduced-order modelling and PDE model discovery. Leveraging the expressive power of deep neural networks, especially in high dimensions, such methods learn the mapping between functional state variables. While proposed methods have assumed noise only in the dependent variables, experimental and numerical data for operator learning typically exhibit noise in the independent variables as well, since both variables represent signals that are subject to measurement error. In regression on scalar data, failure to account for noisy independent variables can lead to biased parameter estimates. With noisy independent variables, linear models fitted via ordinary least squares (OLS) will show attenuation bias, wherein the slope will be underestimated. In this work, we derive an analogue of attenuation bias for linear operator regression with white noise in both the independent and dependent variables. In the nonlinear setting, we computationally demonstrate underprediction of the action of the Burgers operator in the presence of noise in the independent variable. We propose error-in-variables (EiV) models for two operator regression methods, MOR-Physics and DeepONet, and demonstrate that these new models reduce bias in the presence of noisy independent variables for a variety of operator learning problems. Considering the Burgers operator in 1D and 2D, we demonstrate that EiV operator learning robustly recovers operators in high-noise regimes that defeat OLS operator learning. We also introduce an EiV model for time-evolving PDE discovery and show that OLS and EiV perform similarly in learning the Kuramoto-Sivashinsky evolution operator from corrupted data, suggesting that the effect of bias in OLS operator learning depends on the regularity of the target operator.

Probabilistic partition of unity networks: clustering based deep approximation

Partition of unity networks (POU-Nets) have been shown capable of realizing algebraic convergence rates for regression and solution of PDEs, but require empirical tuning of training parameters. We enrich POU-Nets with a Gaussian noise model to obtain a probabilistic generalization amenable to gradient-based minimization of a maximum likelihood loss. The resulting architecture provides spatial representations of both noiseless and noisy data as Gaussian mixtures with closed form expressions for variance which provides an estimator of local error. The training process yields remarkably sharp partitions of input space based upon correlation of function values. This classification of training points is amenable to a hierarchical refinement strategy that significantly improves the localization of the regression, allowing for higher-order polynomial approximation to be utilized. The framework scales more favorably to large data sets as compared to Gaussian process regression and allows for spatially varying uncertainty, leveraging the expressive power of deep neural networks while bypassing expensive training associated with other probabilistic deep learning methods. Compared to standard deep neural networks, the framework demonstrates hp-convergence without the use of regularizers to tune the localization of partitions. We provide benchmarks quantifying performance in high/low-dimensions, demonstrating that convergence rates depend only on the latent dimension of data within high-dimensional space. Finally, we introduce a new open-source data set of PDE-based simulations of a semiconductor device and perform unsupervised extraction of a physically interpretable reduced-order basis.

Gaussian Process Regression constrained by Boundary Value Problems

We develop a framework for Gaussian processes regression constrained by boundary value problems. The framework may be applied to infer the solution of a well-posed boundary value problem with a known second-order differential operator and boundary conditions, but for which only scattered observations of the source term are available. Scattered observations of the solution may also be used in the regression. The framework combines co-kriging with the linear transformation of a Gaussian process together with the use of kernels given by spectral expansions in eigenfunctions of the boundary value problem. Thus, it benefits from a reduced-rank property of covariance matrices. We demonstrate that the resulting framework yields more accurate and stable solution inference as compared to physics-informed Gaussian process regression without boundary condition constraints.

A Survey of Constrained Gaussian Process Regression: Approaches and Implementation Challenges

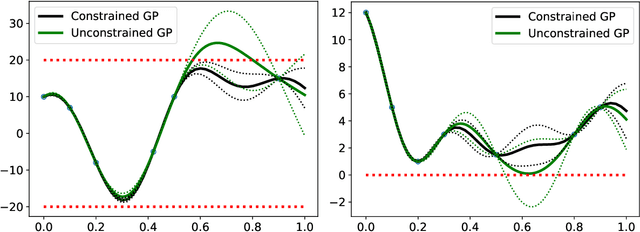
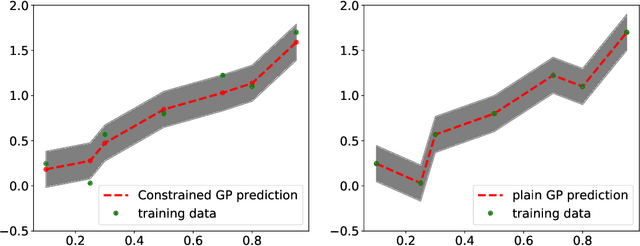
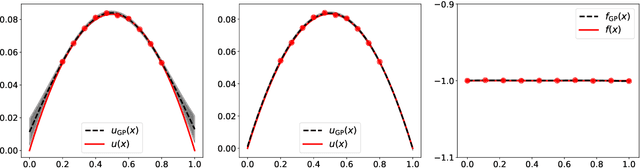
Gaussian process regression is a popular Bayesian framework for surrogate modeling of expensive data sources. As part of a broader effort in scientific machine learning, many recent works have incorporated physical constraints or other a priori information within Gaussian process regression to supplement limited data and regularize the behavior of the model. We provide an overview and survey of several classes of Gaussian process constraints, including positivity or bound constraints, monotonicity and convexity constraints, differential equation constraints provided by linear PDEs, and boundary condition constraints. We compare the strategies behind each approach as well as the differences in implementation, concluding with a discussion of the computational challenges introduced by constraints.

Data-driven learning of robust nonlocal physics from high-fidelity synthetic data

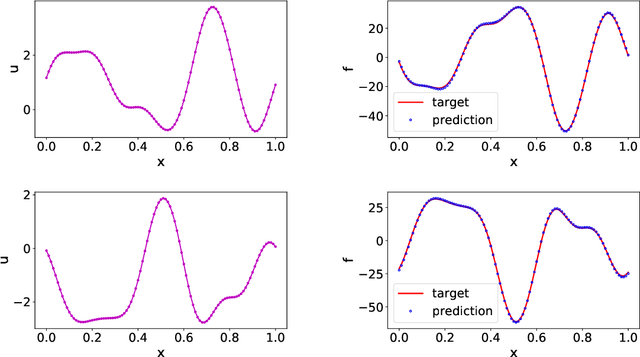
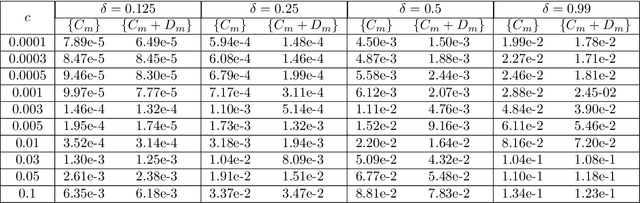
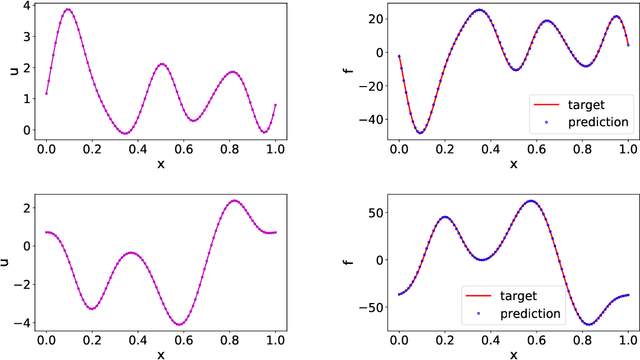
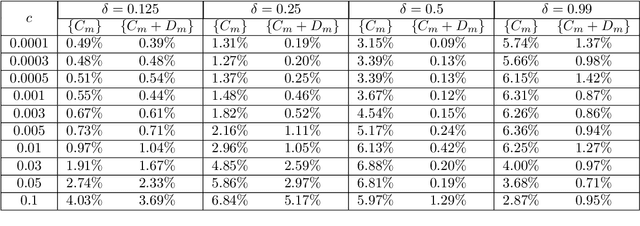
A key challenge to nonlocal models is the analytical complexity of deriving them from first principles, and frequently their use is justified a posteriori. In this work we extract nonlocal models from data, circumventing these challenges and providing data-driven justification for the resulting model form. Extracting provably robust data-driven surrogates is a major challenge for machine learning (ML) approaches, due to nonlinearities and lack of convexity. Our scheme allows extraction of provably invertible nonlocal models whose kernels may be partially negative. To achieve this, based on established nonlocal theory, we embed in our algorithm sufficient conditions on the non-positive part of the kernel that guarantee well-posedness of the learnt operator. These conditions are imposed as inequality constraints and ensure that models are robust, even in small-data regimes. We demonstrate this workflow for a range of applications, including reproduction of manufactured nonlocal kernels; numerical homogenization of Darcy flow associated with a heterogeneous periodic microstructure; nonlocal approximation to high-order local transport phenomena; and approximation of globally supported fractional diffusion operators by truncated kernels.

Machine Learning of Space-Fractional Differential Equations

Data-driven discovery of "hidden physics" -- i.e., machine learning of differential equation models underlying observed data -- has recently been approached by embedding the discovery problem into a Gaussian Process regression of spatial data, treating and discovering unknown equation parameters as hyperparameters of a modified "physics informed" Gaussian Process kernel. This kernel includes the parametrized differential operators applied to a prior covariance kernel. We extend this framework to linear space-fractional differential equations. The methodology is compatible with a wide variety of fractional operators in $\mathbb{R}^d$ and stationary covariance kernels, including the Matern class, and can optimize the Matern parameter during training. We provide a user-friendly and feasible way to perform fractional derivatives of kernels, via a unified set of d-dimensional Fourier integral formulas amenable to generalized Gauss-Laguerre quadrature. The implementation of fractional derivatives has several benefits. First, it allows for discovering fractional-order PDEs for systems characterized by heavy tails or anomalous diffusion, bypassing the analytical difficulty of fractional calculus. Data sets exhibiting such features are of increasing prevalence in physical and financial domains. Second, a single fractional-order archetype allows for a derivative of arbitrary order to be learned, with the order itself being a parameter in the regression. This is advantageous even when used for discovering integer-order equations; the user is not required to assume a "dictionary" of derivatives of various orders, and directly controls the parsimony of the models being discovered. We illustrate on several examples, including fractional-order interpolation of advection-diffusion and modeling relative stock performance in the S&P 500 with alpha-stable motion via a fractional diffusion equation.