Andy Huang
Alexa, Let's Work Together: Introducing the First Alexa Prize TaskBot Challenge on Conversational Task Assistance
Sep 13, 2022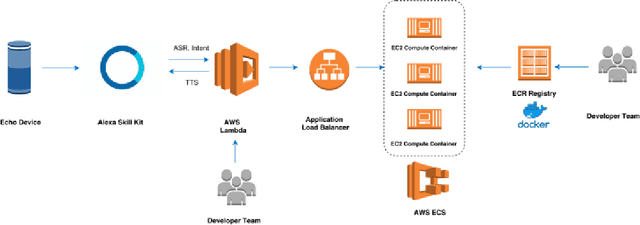
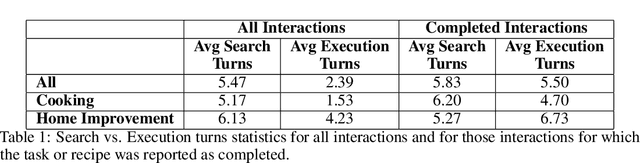
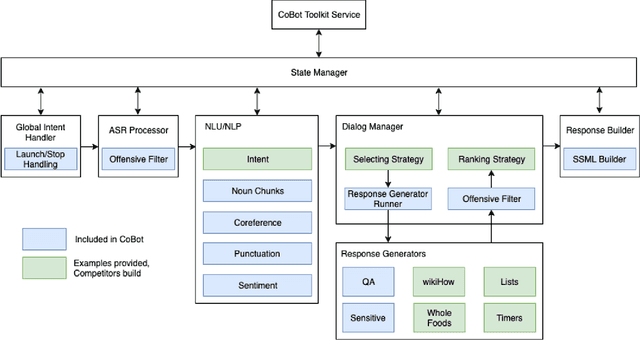

Abstract:Since its inception in 2016, the Alexa Prize program has enabled hundreds of university students to explore and compete to develop conversational agents through the SocialBot Grand Challenge. The goal of the challenge is to build agents capable of conversing coherently and engagingly with humans on popular topics for 20 minutes, while achieving an average rating of at least 4.0/5.0. However, as conversational agents attempt to assist users with increasingly complex tasks, new conversational AI techniques and evaluation platforms are needed. The Alexa Prize TaskBot challenge, established in 2021, builds on the success of the SocialBot challenge by introducing the requirements of interactively assisting humans with real-world Cooking and Do-It-Yourself tasks, while making use of both voice and visual modalities. This challenge requires the TaskBots to identify and understand the user's need, identify and integrate task and domain knowledge into the interaction, and develop new ways of engaging the user without distracting them from the task at hand, among other challenges. This paper provides an overview of the TaskBot challenge, describes the infrastructure support provided to the teams with the CoBot Toolkit, and summarizes the approaches the participating teams took to overcome the research challenges. Finally, it analyzes the performance of the competing TaskBots during the first year of the competition.
Polynomial-Spline Neural Networks with Exact Integrals
Oct 26, 2021Abstract:Using neural networks to solve variational problems, and other scientific machine learning tasks, has been limited by a lack of consistency and an inability to exactly integrate expressions involving neural network architectures. We address these limitations by formulating a novel neural network architecture that combines a polynomial mixture-of-experts model with free knot B1-spline basis functions. Effectively, our architecture performs piecewise polynomial approximation on each cell of a trainable partition of unity. Our architecture exhibits both $h$- and $p$- refinement for regression problems at the convergence rates expected from approximation theory, allowing for consistency in solving variational problems. Moreover, this architecture, its moments, and its partial derivatives can all be integrated exactly, obviating a reliance on sampling or quadrature and enabling error-free computation of variational forms. We demonstrate the success of our network on a range of regression and variational problems that illustrate the consistency and exact integrability of our network architecture.
Probabilistic partition of unity networks: clustering based deep approximation
Jul 07, 2021Abstract:Partition of unity networks (POU-Nets) have been shown capable of realizing algebraic convergence rates for regression and solution of PDEs, but require empirical tuning of training parameters. We enrich POU-Nets with a Gaussian noise model to obtain a probabilistic generalization amenable to gradient-based minimization of a maximum likelihood loss. The resulting architecture provides spatial representations of both noiseless and noisy data as Gaussian mixtures with closed form expressions for variance which provides an estimator of local error. The training process yields remarkably sharp partitions of input space based upon correlation of function values. This classification of training points is amenable to a hierarchical refinement strategy that significantly improves the localization of the regression, allowing for higher-order polynomial approximation to be utilized. The framework scales more favorably to large data sets as compared to Gaussian process regression and allows for spatially varying uncertainty, leveraging the expressive power of deep neural networks while bypassing expensive training associated with other probabilistic deep learning methods. Compared to standard deep neural networks, the framework demonstrates hp-convergence without the use of regularizers to tune the localization of partitions. We provide benchmarks quantifying performance in high/low-dimensions, demonstrating that convergence rates depend only on the latent dimension of data within high-dimensional space. Finally, we introduce a new open-source data set of PDE-based simulations of a semiconductor device and perform unsupervised extraction of a physically interpretable reduced-order basis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge