Ravi G. Patel
Uncertainty quantification of neural network models of evolving processes via Langevin sampling
Apr 21, 2025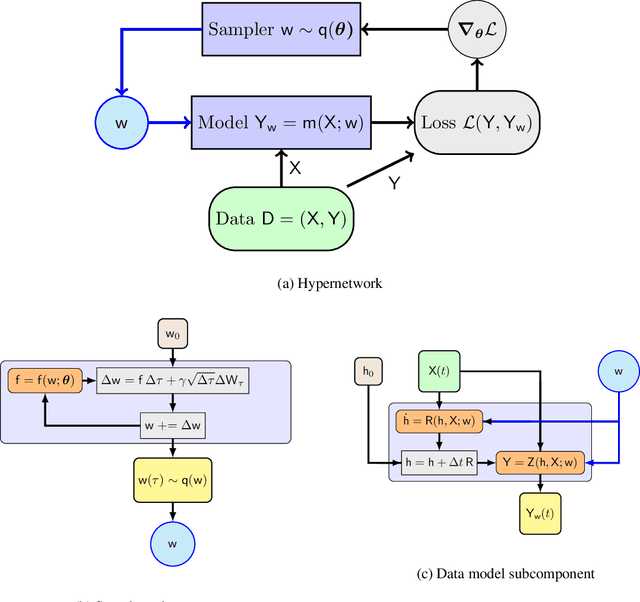
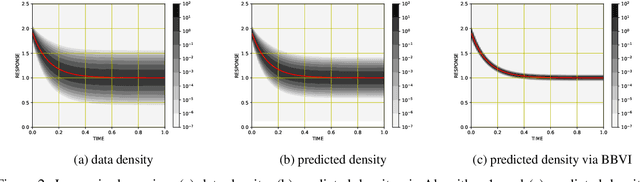
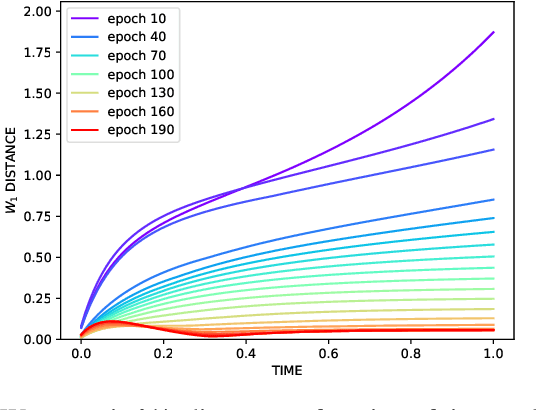
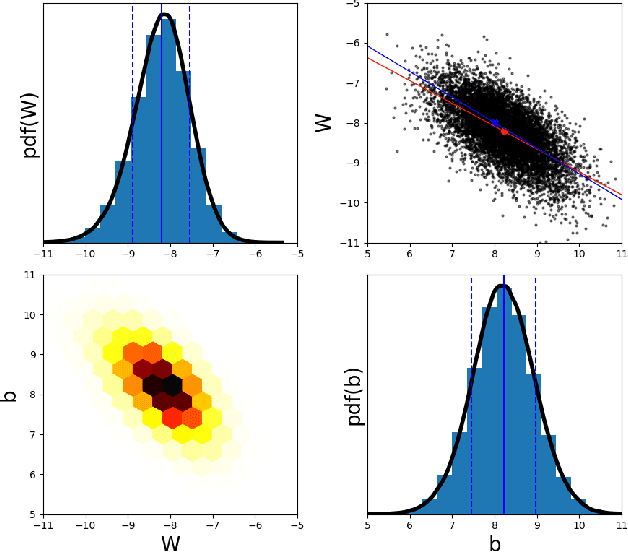
Abstract:We propose a scalable, approximate inference hypernetwork framework for a general model of history-dependent processes. The flexible data model is based on a neural ordinary differential equation (NODE) representing the evolution of internal states together with a trainable observation model subcomponent. The posterior distribution corresponding to the data model parameters (weights and biases) follows a stochastic differential equation with a drift term related to the score of the posterior that is learned jointly with the data model parameters. This Langevin sampling approach offers flexibility in balancing the computational budget between the evaluation cost of the data model and the approximation of the posterior density of its parameters. We demonstrate performance of the hypernetwork on chemical reaction and material physics data and compare it to mean-field variational inference.
Mixture of neural operator experts for learning boundary conditions and model selection
Feb 06, 2025Abstract:While Fourier-based neural operators are best suited to learning mappings between functions on periodic domains, several works have introduced techniques for incorporating non trivial boundary conditions. However, all previously introduced methods have restrictions that limit their applicability. In this work, we introduce an alternative approach to imposing boundary conditions inspired by volume penalization from numerical methods and Mixture of Experts (MoE) from machine learning. By introducing competing experts, the approach additionally allows for model selection. To demonstrate the method, we combine a spatially conditioned MoE with the Fourier based, Modal Operator Regression for Physics (MOR-Physics) neural operator and recover a nonlinear operator on a disk and quarter disk. Next, we extract a large eddy simulation (LES) model from direct numerical simulation of channel flow and show the domain decomposition provided by our approach. Finally, we train our LES model with Bayesian variational inference and obtain posterior predictive samples of flow far past the DNS simulation time horizon.
Analog Bayesian neural networks are insensitive to the shape of the weight distribution
Jan 09, 2025Abstract:Recent work has demonstrated that Bayesian neural networks (BNN's) trained with mean field variational inference (MFVI) can be implemented in analog hardware, promising orders of magnitude energy savings compared to the standard digital implementations. However, while Gaussians are typically used as the variational distribution in MFVI, it is difficult to precisely control the shape of the noise distributions produced by sampling analog devices. This paper introduces a method for MFVI training using real device noise as the variational distribution. Furthermore, we demonstrate empirically that the predictive distributions from BNN's with the same weight means and variances converge to the same distribution, regardless of the shape of the variational distribution. This result suggests that analog device designers do not need to consider the shape of the device noise distribution when hardware-implementing BNNs performing MFVI.
Uncertainty Quantification of Graph Convolution Neural Network Models of Evolving Processes
Feb 17, 2024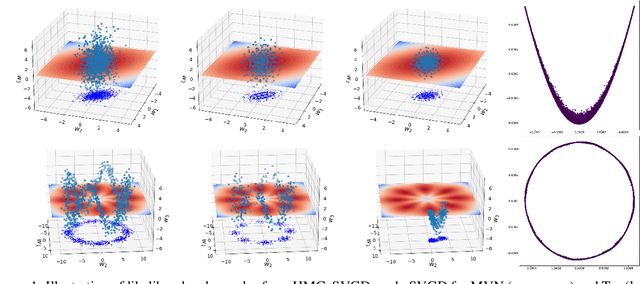
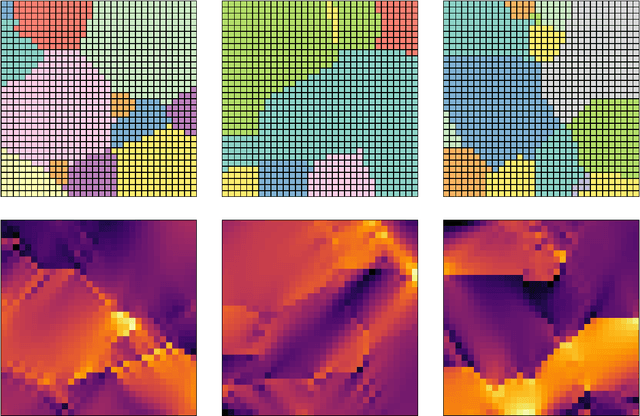
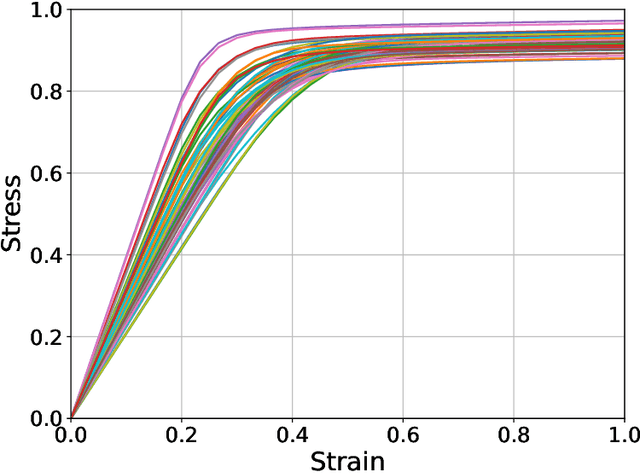
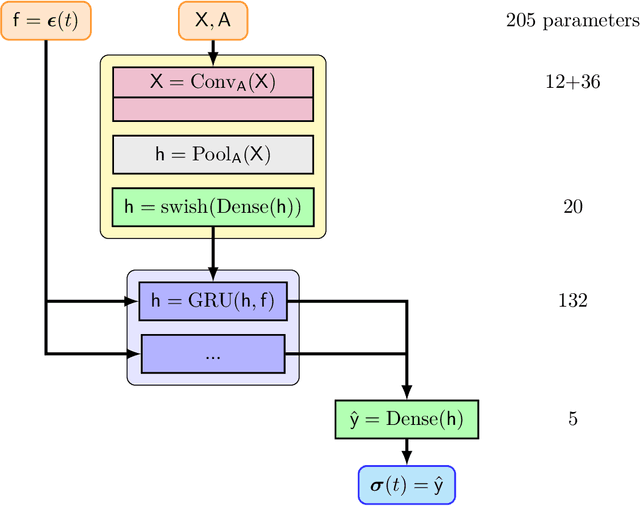
Abstract:The application of neural network models to scientific machine learning tasks has proliferated in recent years. In particular, neural network models have proved to be adept at modeling processes with spatial-temporal complexity. Nevertheless, these highly parameterized models have garnered skepticism in their ability to produce outputs with quantified error bounds over the regimes of interest. Hence there is a need to find uncertainty quantification methods that are suitable for neural networks. In this work we present comparisons of the parametric uncertainty quantification of neural networks modeling complex spatial-temporal processes with Hamiltonian Monte Carlo and Stein variational gradient descent and its projected variant. Specifically we apply these methods to graph convolutional neural network models of evolving systems modeled with recurrent neural network and neural ordinary differential equations architectures. We show that Stein variational inference is a viable alternative to Monte Carlo methods with some clear advantages for complex neural network models. For our exemplars, Stein variational interference gave similar uncertainty profiles through time compared to Hamiltonian Monte Carlo, albeit with generally more generous variance.Projected Stein variational gradient descent also produced similar uncertainty profiles to the non-projected counterpart, but large reductions in the active weight space were confounded by the stability of the neural network predictions and the convoluted likelihood landscape.
Error-in-variables modelling for operator learning
Apr 22, 2022


Abstract:Deep operator learning has emerged as a promising tool for reduced-order modelling and PDE model discovery. Leveraging the expressive power of deep neural networks, especially in high dimensions, such methods learn the mapping between functional state variables. While proposed methods have assumed noise only in the dependent variables, experimental and numerical data for operator learning typically exhibit noise in the independent variables as well, since both variables represent signals that are subject to measurement error. In regression on scalar data, failure to account for noisy independent variables can lead to biased parameter estimates. With noisy independent variables, linear models fitted via ordinary least squares (OLS) will show attenuation bias, wherein the slope will be underestimated. In this work, we derive an analogue of attenuation bias for linear operator regression with white noise in both the independent and dependent variables. In the nonlinear setting, we computationally demonstrate underprediction of the action of the Burgers operator in the presence of noise in the independent variable. We propose error-in-variables (EiV) models for two operator regression methods, MOR-Physics and DeepONet, and demonstrate that these new models reduce bias in the presence of noisy independent variables for a variety of operator learning problems. Considering the Burgers operator in 1D and 2D, we demonstrate that EiV operator learning robustly recovers operators in high-noise regimes that defeat OLS operator learning. We also introduce an EiV model for time-evolving PDE discovery and show that OLS and EiV perform similarly in learning the Kuramoto-Sivashinsky evolution operator from corrupted data, suggesting that the effect of bias in OLS operator learning depends on the regularity of the target operator.
Partition of unity networks: deep hp-approximation
Jan 27, 2021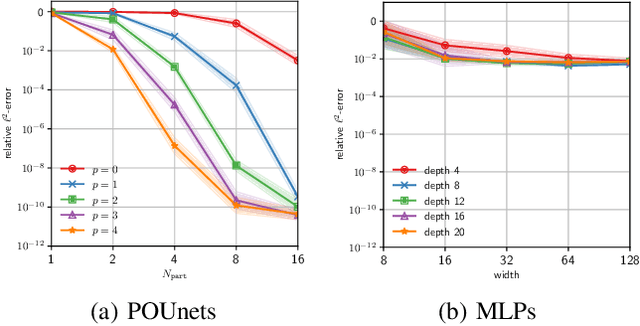
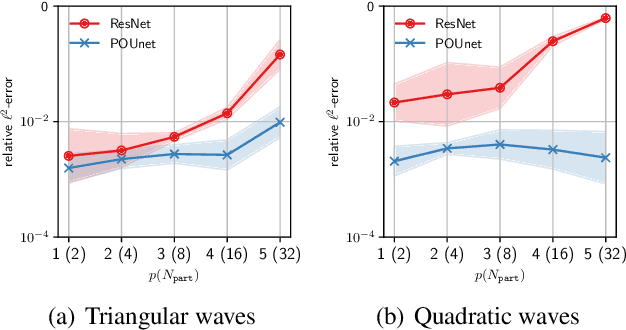
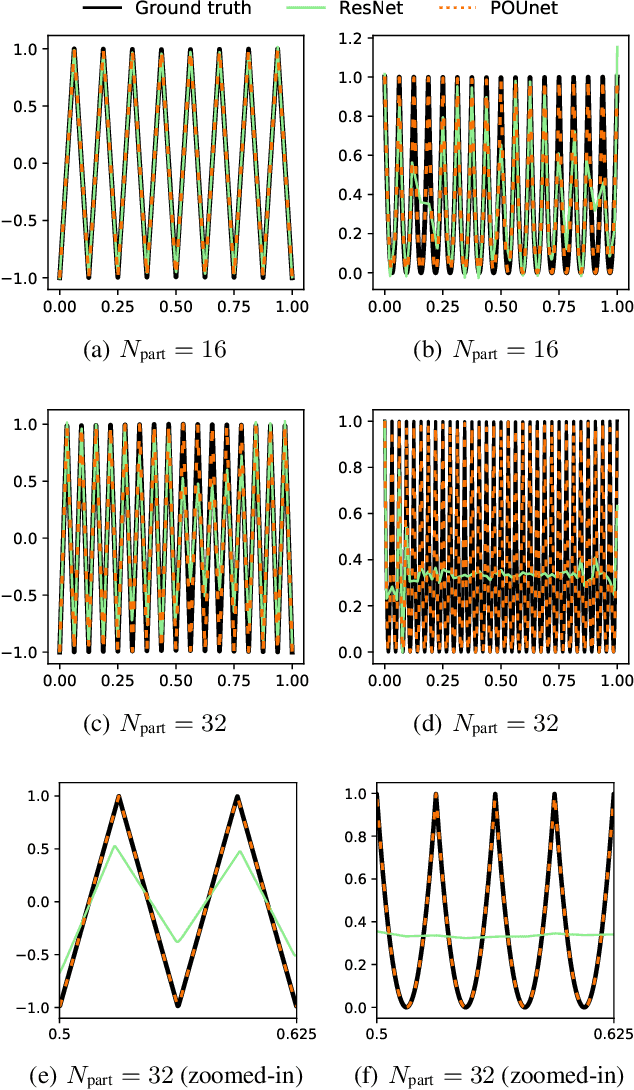
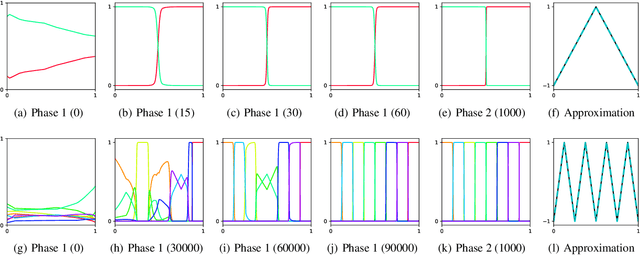
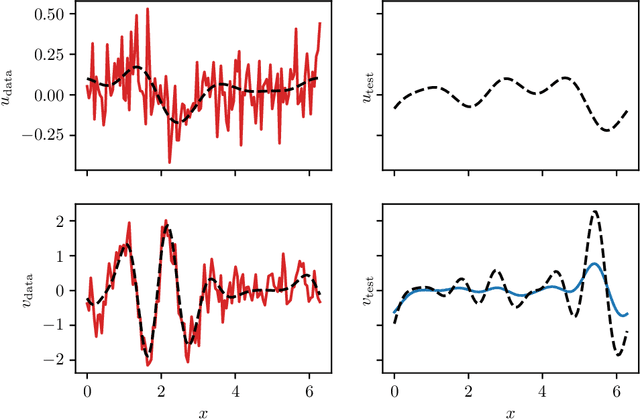
Abstract:Approximation theorists have established best-in-class optimal approximation rates of deep neural networks by utilizing their ability to simultaneously emulate partitions of unity and monomials. Motivated by this, we propose partition of unity networks (POUnets) which incorporate these elements directly into the architecture. Classification architectures of the type used to learn probability measures are used to build a meshfree partition of space, while polynomial spaces with learnable coefficients are associated to each partition. The resulting hp-element-like approximation allows use of a fast least-squares optimizer, and the resulting architecture size need not scale exponentially with spatial dimension, breaking the curse of dimensionality. An abstract approximation result establishes desirable properties to guide network design. Numerical results for two choices of architecture demonstrate that POUnets yield hp-convergence for smooth functions and consistently outperform MLPs for piecewise polynomial functions with large numbers of discontinuities.
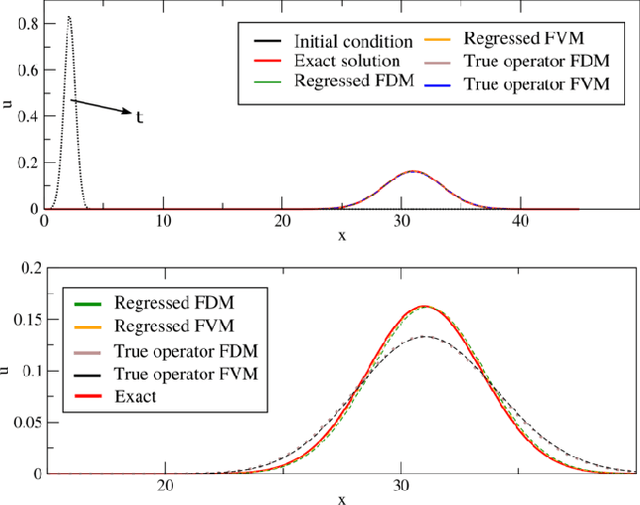
A physics-informed operator regression framework for extracting data-driven continuum models
Sep 25, 2020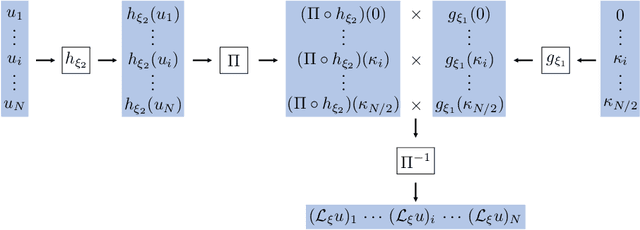

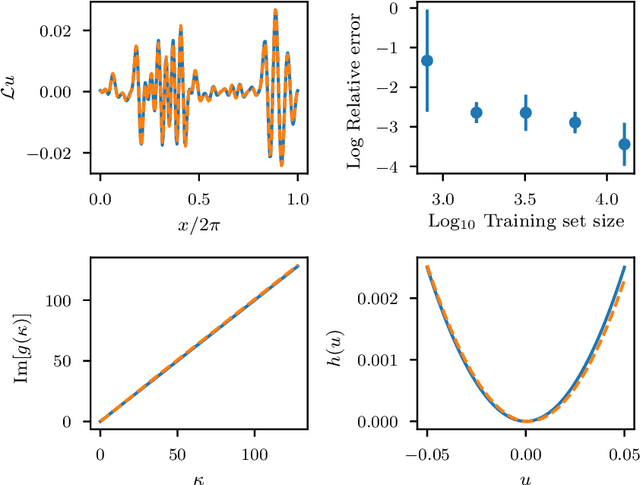

Abstract:The application of deep learning toward discovery of data-driven models requires careful application of inductive biases to obtain a description of physics which is both accurate and robust. We present here a framework for discovering continuum models from high fidelity molecular simulation data. Our approach applies a neural network parameterization of governing physics in modal space, allowing a characterization of differential operators while providing structure which may be used to impose biases related to symmetry, isotropy, and conservation form. We demonstrate the effectiveness of our framework for a variety of physics, including local and nonlocal diffusion processes and single and multiphase flows. For the flow physics we demonstrate this approach leads to a learned operator that generalizes to system characteristics not included in the training sets, such as variable particle sizes, densities, and concentration.
A block coordinate descent optimizer for classification problems exploiting convexity
Jun 17, 2020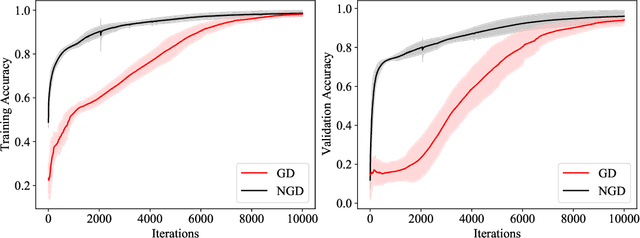
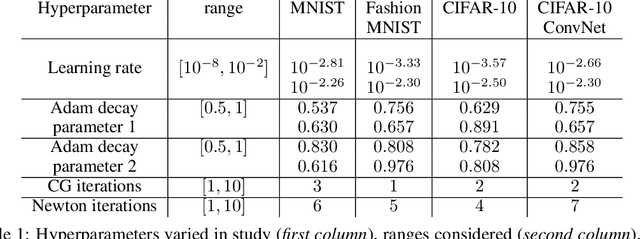
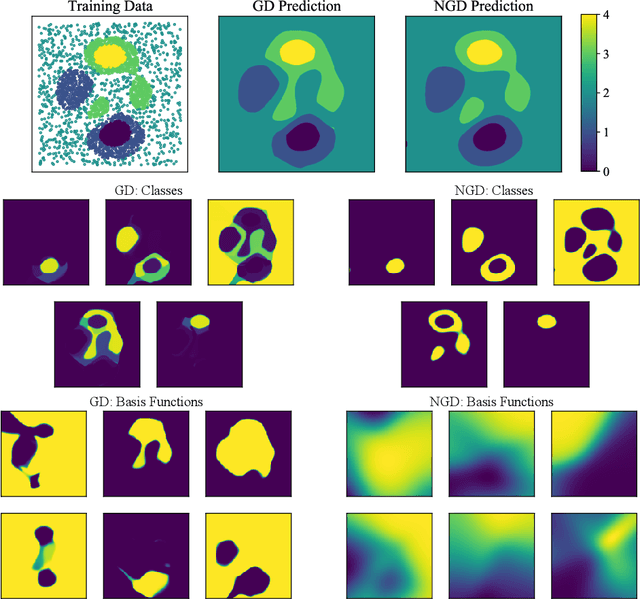
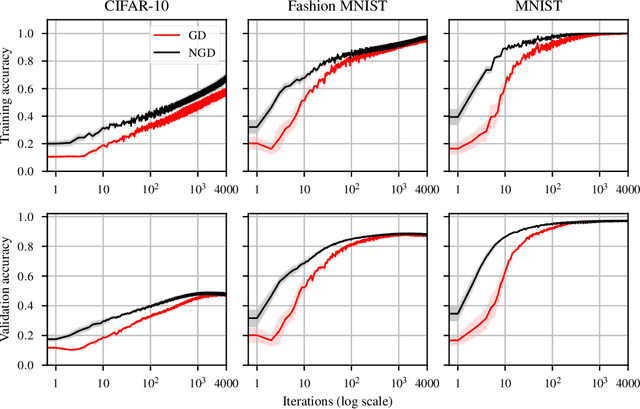
Abstract:Second-order optimizers hold intriguing potential for deep learning, but suffer from increased cost and sensitivity to the non-convexity of the loss surface as compared to gradient-based approaches. We introduce a coordinate descent method to train deep neural networks for classification tasks that exploits global convexity of the cross-entropy loss in the weights of the linear layer. Our hybrid Newton/Gradient Descent (NGD) method is consistent with the interpretation of hidden layers as providing an adaptive basis and the linear layer as providing an optimal fit of the basis to data. By alternating between a second-order method to find globally optimal parameters for the linear layer and gradient descent to train the hidden layers, we ensure an optimal fit of the adaptive basis to data throughout training. The size of the Hessian in the second-order step scales only with the number weights in the linear layer and not the depth and width of the hidden layers; furthermore, the approach is applicable to arbitrary hidden layer architecture. Previous work applying this adaptive basis perspective to regression problems demonstrated significant improvements in accuracy at reduced training cost, and this work can be viewed as an extension of this approach to classification problems. We first prove that the resulting Hessian matrix is symmetric semi-definite, and that the Newton step realizes a global minimizer. By studying classification of manufactured two-dimensional point cloud data, we demonstrate both an improvement in validation error and a striking qualitative difference in the basis functions encoded in the hidden layer when trained using NGD. Application to image classification benchmarks for both dense and convolutional architectures reveals improved training accuracy, suggesting possible gains of second-order methods over gradient descent.
Robust Training and Initialization of Deep Neural Networks: An Adaptive Basis Viewpoint
Dec 10, 2019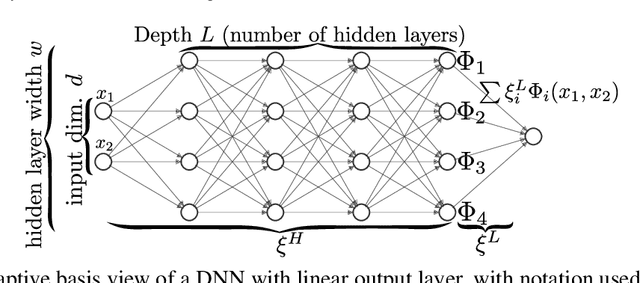
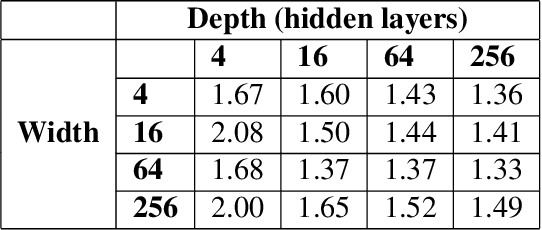
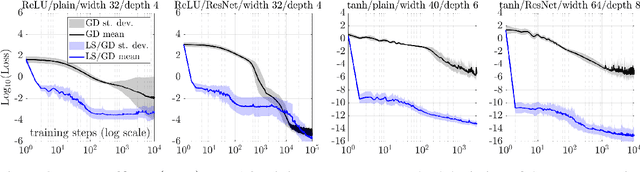
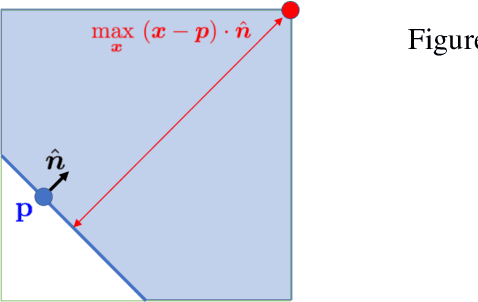
Abstract:Motivated by the gap between theoretical optimal approximation rates of deep neural networks (DNNs) and the accuracy realized in practice, we seek to improve the training of DNNs. The adoption of an adaptive basis viewpoint of DNNs leads to novel initializations and a hybrid least squares/gradient descent optimizer. We provide analysis of these techniques and illustrate via numerical examples dramatic increases in accuracy and convergence rate for benchmarks characterizing scientific applications where DNNs are currently used, including regression problems and physics-informed neural networks for the solution of partial differential equations.
GMLS-Nets: A framework for learning from unstructured data
Sep 13, 2019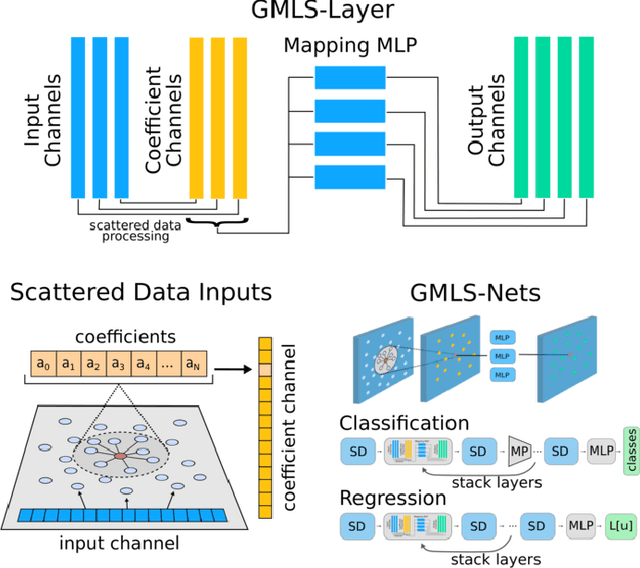
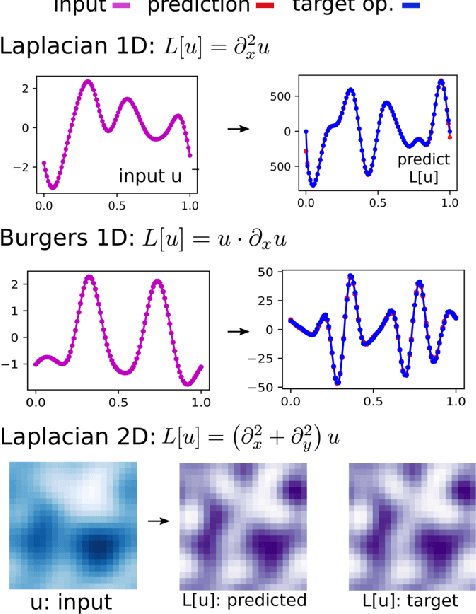
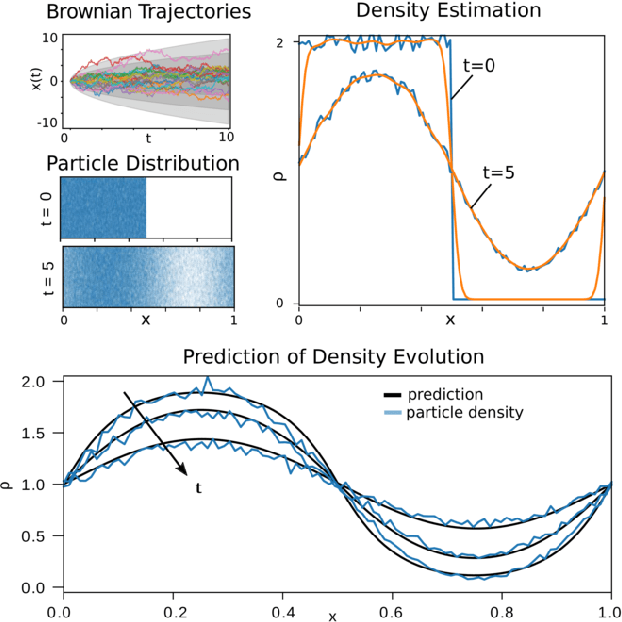
Abstract:Data fields sampled on irregularly spaced points arise in many applications in the sciences and engineering. For regular grids, Convolutional Neural Networks (CNNs) have been successfully used to gaining benefits from weight sharing and invariances. We generalize CNNs by introducing methods for data on unstructured point clouds based on Generalized Moving Least Squares (GMLS). GMLS is a non-parametric technique for estimating linear bounded functionals from scattered data, and has recently been used in the literature for solving partial differential equations. By parameterizing the GMLS estimator, we obtain learning methods for operators with unstructured stencils. In GMLS-Nets the necessary calculations are local, readily parallelizable, and the estimator is supported by a rigorous approximation theory. We show how the framework may be used for unstructured physical data sets to perform functional regression to identify associated differential operators and to regress quantities of interest. The results suggest the architectures to be an attractive foundation for data-driven model development in scientific machine learning applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge