Analog Bayesian neural networks are insensitive to the shape of the weight distribution

Recent work has demonstrated that Bayesian neural networks (BNN's) trained with mean field variational inference (MFVI) can be implemented in analog hardware, promising orders of magnitude energy savings compared to the standard digital implementations. However, while Gaussians are typically used as the variational distribution in MFVI, it is difficult to precisely control the shape of the noise distributions produced by sampling analog devices. This paper introduces a method for MFVI training using real device noise as the variational distribution. Furthermore, we demonstrate empirically that the predictive distributions from BNN's with the same weight means and variances converge to the same distribution, regardless of the shape of the variational distribution. This result suggests that analog device designers do not need to consider the shape of the device noise distribution when hardware-implementing BNNs performing MFVI.

Analog fast Fourier transforms for scalable and efficient signal processing

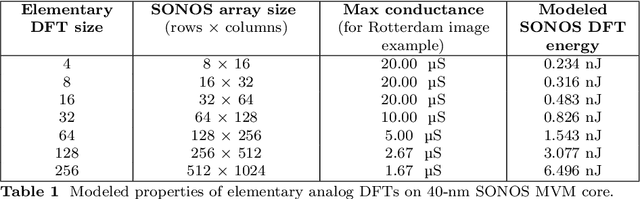
Edge devices are being deployed at increasing volumes to sense and act on information from the physical world. The discrete Fourier transform (DFT) is often necessary to make this sensed data suitable for further processing $\unicode{x2013}$ such as by artificial intelligence (AI) algorithms $\unicode{x2013}$ and for transmission over communication networks. Analog in-memory computing has been shown to be a fast and energy-efficient solution for processing edge AI workloads, but not for Fourier transforms. This is because of the existence of the fast Fourier transform (FFT) algorithm, which enormously reduces the complexity of the DFT but has so far belonged only to digital processors. Here, we show that the FFT can be mapped to analog in-memory computing systems, enabling them to efficiently scale to arbitrarily large Fourier transforms without requiring large sizes or large numbers of non-volatile memory arrays. We experimentally demonstrate analog FFTs on 1D audio and 2D image signals, using a large-scale charge-trapping memory array with precisely tunable, low-conductance analog states. The scalability of both the new analog FFT approach and the charge-trapping memory device is leveraged to compute a 65,536-point analog DFT, a scale that is otherwise inaccessible by analog systems and which is $>$1000$\times$ larger than any previous analog DFT demonstration. The analog FFT also provides more numerically precise DFTs with greater tolerance to device and circuit non-idealities than a direct matrix-vector multiplication approach. We show that the extension of the FFT algorithm to analog in-memory processors leads to design considerations that differ markedly from digital implementations, and that analog Fourier transforms have a substantial power efficiency advantage at all size scales over FFTs implemented on state-of-the-art digital hardware.

An out-of-distribution discriminator based on Bayesian neural network epistemic uncertainty

Neural networks have revolutionized the field of machine learning with increased predictive capability. In addition to improving the predictions of neural networks, there is a simultaneous demand for reliable uncertainty quantification on estimates made by machine learning methods such as neural networks. Bayesian neural networks (BNNs) are an important type of neural network with built-in capability for quantifying uncertainty. This paper discusses aleatoric and epistemic uncertainty in BNNs and how they can be calculated. With an example dataset of images where the goal is to identify the amplitude of an event in the image, it is shown that epistemic uncertainty tends to be lower in images which are well-represented in the training dataset and tends to be high in images which are not well-represented. An algorithm for out-of-distribution (OoD) detection with BNN epistemic uncertainty is introduced along with various experiments demonstrating factors influencing the OoD detection capability in a BNN. The OoD detection capability with epistemic uncertainty is shown to be comparable to the OoD detection in the discriminator network of a generative adversarial network (GAN) with comparable network architecture.

On the Accuracy of Analog Neural Network Inference Accelerators

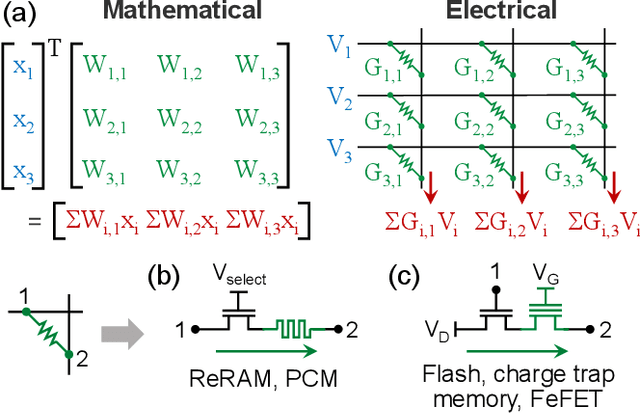
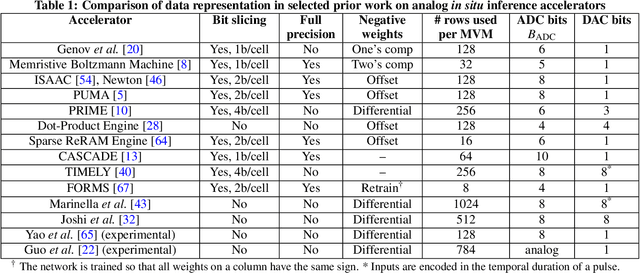
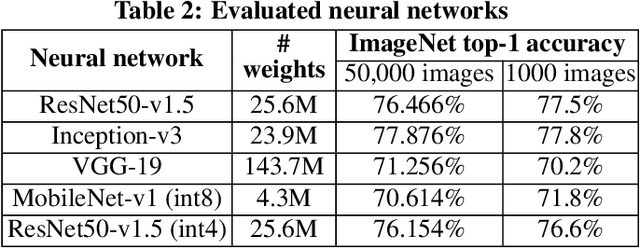
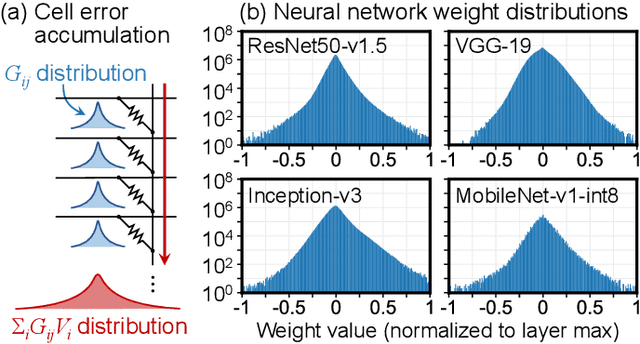
Specialized accelerators have recently garnered attention as a method to reduce the power consumption of neural network inference. A promising category of accelerators utilizes nonvolatile memory arrays to both store weights and perform $\textit{in situ}$ analog computation inside the array. While prior work has explored the design space of analog accelerators to optimize performance and energy efficiency, there is seldom a rigorous evaluation of the accuracy of these accelerators. This work shows how architectural design decisions, particularly in mapping neural network parameters to analog memory cells, influence inference accuracy. When evaluated using ResNet50 on ImageNet, the resilience of the system to analog non-idealities - cell programming errors, analog-to-digital converter resolution, and array parasitic resistances - all improve when analog quantities in the hardware are made proportional to the weights in the network. Moreover, contrary to the assumptions of prior work, nearly equivalent resilience to cell imprecision can be achieved by fully storing weights as analog quantities, rather than spreading weight bits across multiple devices, often referred to as bit slicing. By exploiting proportionality, analog system designers have the freedom to match the precision of the hardware to the needs of the algorithm, rather than attempting to guarantee the same level of precision in the intermediate results as an equivalent digital accelerator. This ultimately results in an analog accelerator that is more accurate, more robust to analog errors, and more energy-efficient.

Device-aware inference operations in SONOS nonvolatile memory arrays

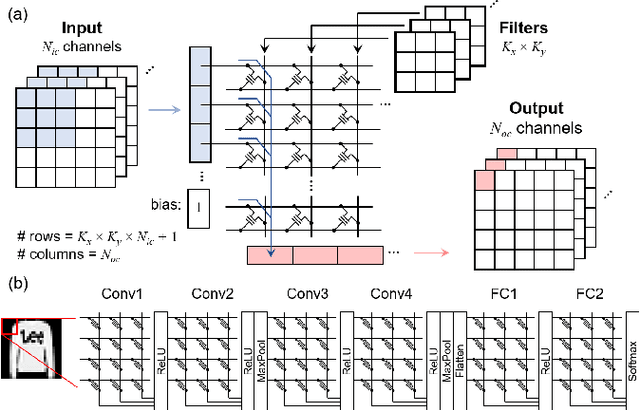
Non-volatile memory arrays can deploy pre-trained neural network models for edge inference. However, these systems are affected by device-level noise and retention issues. Here, we examine damage caused by these effects, introduce a mitigation strategy, and demonstrate its use in fabricated array of SONOS (Silicon-Oxide-Nitride-Oxide-Silicon) devices. On MNIST, fashion-MNIST, and CIFAR-10 tasks, our approach increases resilience to synaptic noise and drift. We also show strong performance can be realized with ADCs of 5-8 bits precision.

Evaluating complexity and resilience trade-offs in emerging memory inference machines

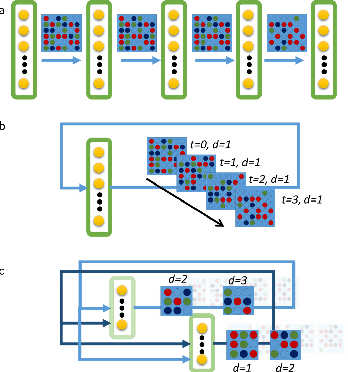
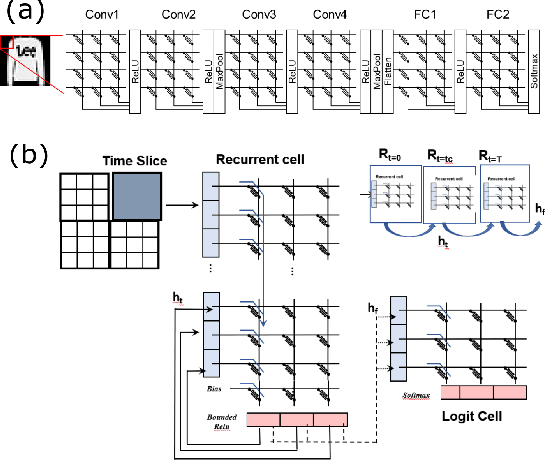
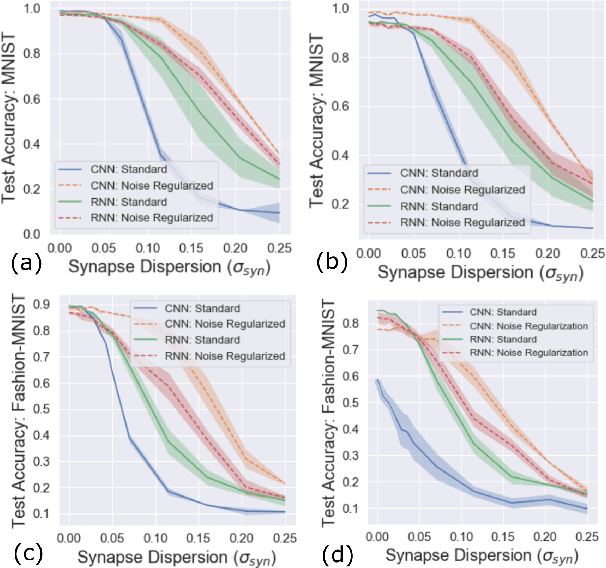
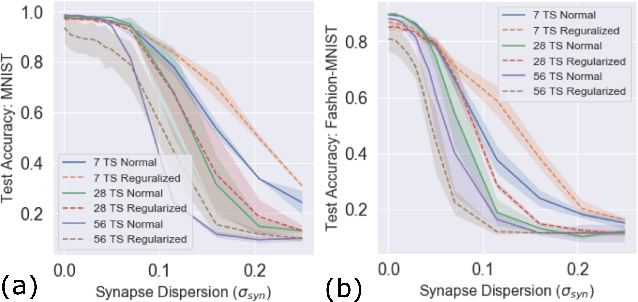
Neuromorphic-style inference only works well if limited hardware resources are maximized properly, e.g. accuracy continues to scale with parameters and complexity in the face of potential disturbance. In this work, we use realistic crossbar simulations to highlight that compact implementations of deep neural networks are unexpectedly susceptible to collapse from multiple system disturbances. Our work proposes a middle path towards high performance and strong resilience utilizing the Mosaics framework, and specifically by re-using synaptic connections in a recurrent neural network implementation that possesses a natural form of noise-immunity.

Multiscale Co-Design Analysis of Energy, Latency, Area, and Accuracy of a ReRAM Analog Neural Training Accelerator

Neural networks are an increasingly attractive algorithm for natural language processing and pattern recognition. Deep networks with >50M parameters are made possible by modern GPU clusters operating at <50 pJ per op and more recently, production accelerators capable of <5pJ per operation at the board level. However, with the slowing of CMOS scaling, new paradigms will be required to achieve the next several orders of magnitude in performance per watt gains. Using an analog resistive memory (ReRAM) crossbar to perform key matrix operations in an accelerator is an attractive option. This work presents a detailed design using a state of the art 14/16 nm PDK for of an analog crossbar circuit block designed to process three key kernels required in training and inference of neural networks. A detailed circuit and device-level analysis of energy, latency, area, and accuracy are given and compared to relevant designs using standard digital ReRAM and SRAM operations. It is shown that the analog accelerator has a 270x energy and 540x latency advantage over a similar block utilizing only digital ReRAM and takes only 11 fJ per multiply and accumulate (MAC). Compared to an SRAM based accelerator, the energy is 430X better and latency is 34X better. Although training accuracy is degraded in the analog accelerator, several options to improve this are presented. The possible gains over a similar digital-only version of this accelerator block suggest that continued optimization of analog resistive memories is valuable. This detailed circuit and device analysis of a training accelerator may serve as a foundation for further architecture-level studies.

Probability Series Expansion Classifier that is Interpretable by Design

This work presents a new classifier that is specifically designed to be fully interpretable. This technique determines the probability of a class outcome, based directly on probability assignments measured from the training data. The accuracy of the predicted probability can be improved by measuring more probability estimates from the training data to create a series expansion that refines the predicted probability. We use this work to classify four standard datasets and achieve accuracies comparable to that of Random Forests. Because this technique is interpretable by design, it is capable of determining the combinations of features that contribute to a particular classification probability for individual cases as well as the weightings of each of combination of features.