Analog fast Fourier transforms for scalable and efficient signal processing
Paper and Code
Sep 27, 2024
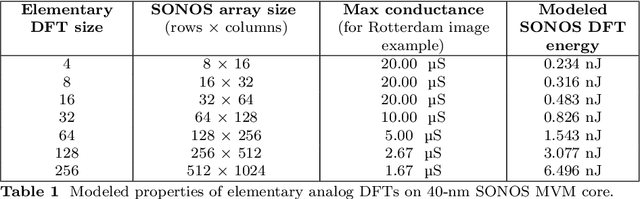


Edge devices are being deployed at increasing volumes to sense and act on information from the physical world. The discrete Fourier transform (DFT) is often necessary to make this sensed data suitable for further processing $\unicode{x2013}$ such as by artificial intelligence (AI) algorithms $\unicode{x2013}$ and for transmission over communication networks. Analog in-memory computing has been shown to be a fast and energy-efficient solution for processing edge AI workloads, but not for Fourier transforms. This is because of the existence of the fast Fourier transform (FFT) algorithm, which enormously reduces the complexity of the DFT but has so far belonged only to digital processors. Here, we show that the FFT can be mapped to analog in-memory computing systems, enabling them to efficiently scale to arbitrarily large Fourier transforms without requiring large sizes or large numbers of non-volatile memory arrays. We experimentally demonstrate analog FFTs on 1D audio and 2D image signals, using a large-scale charge-trapping memory array with precisely tunable, low-conductance analog states. The scalability of both the new analog FFT approach and the charge-trapping memory device is leveraged to compute a 65,536-point analog DFT, a scale that is otherwise inaccessible by analog systems and which is $>$1000$\times$ larger than any previous analog DFT demonstration. The analog FFT also provides more numerically precise DFTs with greater tolerance to device and circuit non-idealities than a direct matrix-vector multiplication approach. We show that the extension of the FFT algorithm to analog in-memory processors leads to design considerations that differ markedly from digital implementations, and that analog Fourier transforms have a substantial power efficiency advantage at all size scales over FFTs implemented on state-of-the-art digital hardware.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge