A Likelihood-Free Approach to Goal-Oriented Bayesian Optimal Experimental Design

Conventional Bayesian optimal experimental design seeks to maximize the expected information gain (EIG) on model parameters. However, the end goal of the experiment often is not to learn the model parameters, but to predict downstream quantities of interest (QoIs) that depend on the learned parameters. And designs that offer high EIG for parameters may not translate to high EIG for QoIs. Goal-oriented optimal experimental design (GO-OED) thus directly targets to maximize the EIG of QoIs. We introduce LF-GO-OED (likelihood-free goal-oriented optimal experimental design), a computational method for conducting GO-OED with nonlinear observation and prediction models. LF-GO-OED is specifically designed to accommodate implicit models, where the likelihood is intractable. In particular, it builds a density ratio estimator from samples generated from approximate Bayesian computation (ABC), thereby sidestepping the need for likelihood evaluations or density estimations. The overall method is validated on benchmark problems with existing methods, and demonstrated on scientific applications of epidemiology and neural science.

Deep Koopman-based Control of Quality Variation in Multistage Manufacturing Systems

This paper presents a modeling-control synthesis to address the quality control challenges in multistage manufacturing systems (MMSs). A new feedforward control scheme is developed to minimize the quality variations caused by process disturbances in MMSs. Notably, the control framework leverages a stochastic deep Koopman (SDK) model to capture the quality propagation mechanism in the MMSs, highlighted by its ability to transform the nonlinear propagation dynamics into a linear one. Two roll-to-roll case studies are presented to validate the proposed method and demonstrate its effectiveness. The overall method is suitable for nonlinear MMSs and does not require extensive expert knowledge.

Goal-Oriented Bayesian Optimal Experimental Design for Nonlinear Models using Markov Chain Monte Carlo

Optimal experimental design (OED) provides a systematic approach to quantify and maximize the value of experimental data. Under a Bayesian approach, conventional OED maximizes the expected information gain (EIG) on model parameters. However, we are often interested in not the parameters themselves, but predictive quantities of interest (QoIs) that depend on the parameters in a nonlinear manner. We present a computational framework of predictive goal-oriented OED (GO-OED) suitable for nonlinear observation and prediction models, which seeks the experimental design providing the greatest EIG on the QoIs. In particular, we propose a nested Monte Carlo estimator for the QoI EIG, featuring Markov chain Monte Carlo for posterior sampling and kernel density estimation for evaluating the posterior-predictive density and its Kullback-Leibler divergence from the prior-predictive. The GO-OED design is then found by maximizing the EIG over the design space using Bayesian optimization. We demonstrate the effectiveness of the overall nonlinear GO-OED method, and illustrate its differences versus conventional non-GO-OED, through various test problems and an application of sensor placement for source inversion in a convection-diffusion field.

Uncertainty Quantification of Graph Convolution Neural Network Models of Evolving Processes

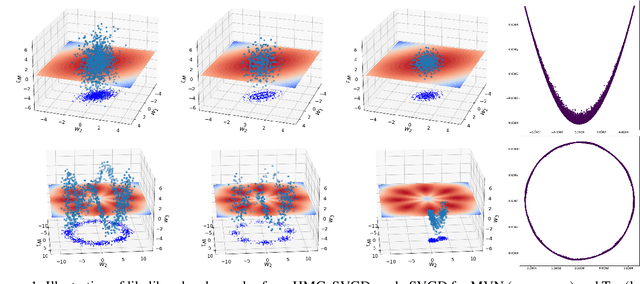
The application of neural network models to scientific machine learning tasks has proliferated in recent years. In particular, neural network models have proved to be adept at modeling processes with spatial-temporal complexity. Nevertheless, these highly parameterized models have garnered skepticism in their ability to produce outputs with quantified error bounds over the regimes of interest. Hence there is a need to find uncertainty quantification methods that are suitable for neural networks. In this work we present comparisons of the parametric uncertainty quantification of neural networks modeling complex spatial-temporal processes with Hamiltonian Monte Carlo and Stein variational gradient descent and its projected variant. Specifically we apply these methods to graph convolutional neural network models of evolving systems modeled with recurrent neural network and neural ordinary differential equations architectures. We show that Stein variational inference is a viable alternative to Monte Carlo methods with some clear advantages for complex neural network models. For our exemplars, Stein variational interference gave similar uncertainty profiles through time compared to Hamiltonian Monte Carlo, albeit with generally more generous variance.Projected Stein variational gradient descent also produced similar uncertainty profiles to the non-projected counterpart, but large reductions in the active weight space were confounded by the stability of the neural network predictions and the convoluted likelihood landscape.

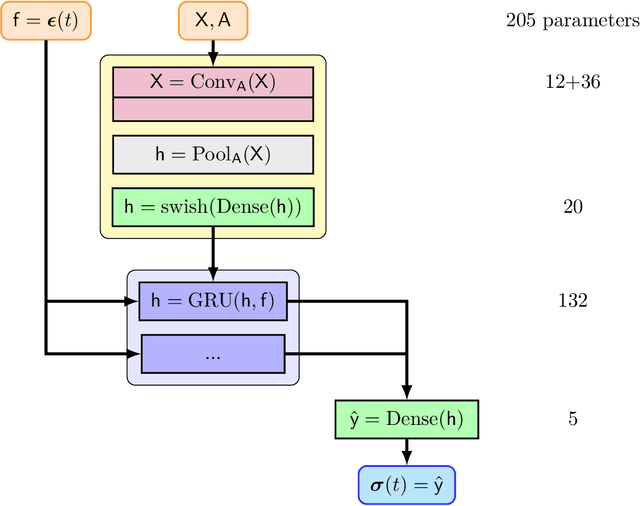
Enhancing Dynamical System Modeling through Interpretable Machine Learning Augmentations: A Case Study in Cathodic Electrophoretic Deposition

We introduce a comprehensive data-driven framework aimed at enhancing the modeling of physical systems, employing inference techniques and machine learning enhancements. As a demonstrative application, we pursue the modeling of cathodic electrophoretic deposition (EPD), commonly known as e-coating. Our approach illustrates a systematic procedure for enhancing physical models by identifying their limitations through inference on experimental data and introducing adaptable model enhancements to address these shortcomings. We begin by tackling the issue of model parameter identifiability, which reveals aspects of the model that require improvement. To address generalizability , we introduce modifications which also enhance identifiability. However, these modifications do not fully capture essential experimental behaviors. To overcome this limitation, we incorporate interpretable yet flexible augmentations into the baseline model. These augmentations are parameterized by simple fully-connected neural networks (FNNs), and we leverage machine learning tools, particularly Neural Ordinary Differential Equations (Neural ODEs), to learn these augmentations. Our simulations demonstrate that the machine learning-augmented model more accurately captures observed behaviors and improves predictive accuracy. Nevertheless, we contend that while the model updates offer superior performance and capture the relevant physics, we can reduce off-line computational costs by eliminating certain dynamics without compromising accuracy or interpretability in downstream predictions of quantities of interest, particularly film thickness predictions. The entire process outlined here provides a structured approach to leverage data-driven methods. Firstly, it helps us comprehend the root causes of model inaccuracies, and secondly, it offers a principled method for enhancing model performance.

Stochastic Deep Koopman Model for Quality Propagation Analysis in Multistage Manufacturing Systems

The modeling of multistage manufacturing systems (MMSs) has attracted increased attention from both academia and industry. Recent advancements in deep learning methods provide an opportunity to accomplish this task with reduced cost and expertise. This study introduces a stochastic deep Koopman (SDK) framework to model the complex behavior of MMSs. Specifically, we present a novel application of Koopman operators to propagate critical quality information extracted by variational autoencoders. Through this framework, we can effectively capture the general nonlinear evolution of product quality using a transferred linear representation, thus enhancing the interpretability of the data-driven model. To evaluate the performance of the SDK framework, we carried out a comparative study on an open-source dataset. The main findings of this paper are as follows. Our results indicate that SDK surpasses other popular data-driven models in accuracy when predicting stagewise product quality within the MMS. Furthermore, the unique linear propagation property in the stochastic latent space of SDK enables traceability for quality evolution throughout the process, thereby facilitating the design of root cause analysis schemes. Notably, the proposed framework requires minimal knowledge of the underlying physics of production lines. It serves as a virtual metrology tool that can be applied to various MMSs, contributing to the ultimate goal of Zero Defect Manufacturing.

FP-IRL: Fokker-Planck-based Inverse Reinforcement Learning -- A Physics-Constrained Approach to Markov Decision Processes

Inverse Reinforcement Learning (IRL) is a compelling technique for revealing the rationale underlying the behavior of autonomous agents. IRL seeks to estimate the unknown reward function of a Markov decision process (MDP) from observed agent trajectories. However, IRL needs a transition function, and most algorithms assume it is known or can be estimated in advance from data. It therefore becomes even more challenging when such transition dynamics is not known a-priori, since it enters the estimation of the policy in addition to determining the system's evolution. When the dynamics of these agents in the state-action space is described by stochastic differential equations (SDE) in It^{o} calculus, these transitions can be inferred from the mean-field theory described by the Fokker-Planck (FP) equation. We conjecture there exists an isomorphism between the time-discrete FP and MDP that extends beyond the minimization of free energy (in FP) and maximization of the reward (in MDP). We identify specific manifestations of this isomorphism and use them to create a novel physics-aware IRL algorithm, FP-IRL, which can simultaneously infer the transition and reward functions using only observed trajectories. We employ variational system identification to infer the potential function in FP, which consequently allows the evaluation of reward, transition, and policy by leveraging the conjecture. We demonstrate the effectiveness of FP-IRL by applying it to a synthetic benchmark and a biological problem of cancer cell dynamics, where the transition function is inaccessible.

Variational Sequential Optimal Experimental Design using Reinforcement Learning

We introduce variational sequential Optimal Experimental Design (vsOED), a new method for optimally designing a finite sequence of experiments under a Bayesian framework and with information-gain utilities. Specifically, we adopt a lower bound estimator for the expected utility through variational approximation to the Bayesian posteriors. The optimal design policy is solved numerically by simultaneously maximizing the variational lower bound and performing policy gradient updates. We demonstrate this general methodology for a range of OED problems targeting parameter inference, model discrimination, and goal-oriented prediction. These cases encompass explicit and implicit likelihoods, nuisance parameters, and physics-based partial differential equation models. Our vsOED results indicate substantially improved sample efficiency and reduced number of forward model simulations compared to previous sequential design algorithms.

Uncertainty Quantification in Machine Learning for Engineering Design and Health Prognostics: A Tutorial

On top of machine learning models, uncertainty quantification (UQ) functions as an essential layer of safety assurance that could lead to more principled decision making by enabling sound risk assessment and management. The safety and reliability improvement of ML models empowered by UQ has the potential to significantly facilitate the broad adoption of ML solutions in high-stakes decision settings, such as healthcare, manufacturing, and aviation, to name a few. In this tutorial, we aim to provide a holistic lens on emerging UQ methods for ML models with a particular focus on neural networks and the applications of these UQ methods in tackling engineering design as well as prognostics and health management problems. Toward this goal, we start with a comprehensive classification of uncertainty types, sources, and causes pertaining to UQ of ML models. Next, we provide a tutorial-style description of several state-of-the-art UQ methods: Gaussian process regression, Bayesian neural network, neural network ensemble, and deterministic UQ methods focusing on spectral-normalized neural Gaussian process. Established upon the mathematical formulations, we subsequently examine the soundness of these UQ methods quantitatively and qualitatively (by a toy regression example) to examine their strengths and shortcomings from different dimensions. Then, we review quantitative metrics commonly used to assess the quality of predictive uncertainty in classification and regression problems. Afterward, we discuss the increasingly important role of UQ of ML models in solving challenging problems in engineering design and health prognostics. Two case studies with source codes available on GitHub are used to demonstrate these UQ methods and compare their performance in the life prediction of lithium-ion batteries at the early stage and the remaining useful life prediction of turbofan engines.

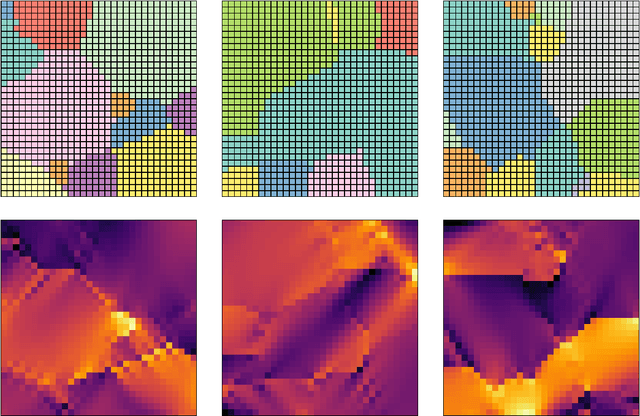
Shapley-based Explainable AI for Clustering Applications in Fault Diagnosis and Prognosis

Data-driven artificial intelligence models require explainability in intelligent manufacturing to streamline adoption and trust in modern industry. However, recently developed explainable artificial intelligence (XAI) techniques that estimate feature contributions on a model-agnostic level such as SHapley Additive exPlanations (SHAP) have not yet been evaluated for semi-supervised fault diagnosis and prognosis problems characterized by class imbalance and weakly labeled datasets. This paper explores the potential of utilizing Shapley values for a new clustering framework compatible with semi-supervised learning problems, loosening the strict supervision requirement of current XAI techniques. This broad methodology is validated on two case studies: a heatmap image dataset obtained from a semiconductor manufacturing process featuring class imbalance, and a benchmark dataset utilized in the 2021 Prognostics and Health Management (PHM) Data Challenge. Semi-supervised clustering based on Shapley values significantly improves upon clustering quality compared to the fully unsupervised case, deriving information-dense and meaningful clusters that relate to underlying fault diagnosis model predictions. These clusters can also be characterized by high-precision decision rules in terms of original feature values, as demonstrated in the second case study. The rules, limited to 1-2 terms utilizing original feature scales, describe 12 out of the 16 derived equipment failure clusters with precision exceeding 0.85, showcasing the promising utility of the explainable clustering framework for intelligent manufacturing applications.