Flow matching Operators for Residual-Augmented Probabilistic Learning of Partial Differential Equations

Learning probabilistic surrogates for partial differential equations remains challenging in data-scarce regimes: neural operators require large amounts of high-fidelity data, while generative approaches typically sacrifice resolution invariance. We formulate flow matching in an infinite-dimensional function space to learn a probabilistic transport that maps low-fidelity approximations to the manifold of high-fidelity PDE solutions via learned residual corrections. We develop a conditional neural operator architecture based on feature-wise linear modulation for flow matching vector fields directly in function space, enabling inference at arbitrary spatial resolutions without retraining. To improve stability and representational control of the induced neural ODE, we parameterize the flow vector field as a sum of a linear operator and a nonlinear operator, combining lightweight linear components with a conditioned Fourier neural operator for expressive, input-dependent dynamics. We then formulate a residual-augmented learning strategy where the flow model learns probabilistic corrections from inexpensive low-fidelity surrogates to high-fidelity solutions, rather than learning the full solution mapping from scratch. Finally, we derive tractable training objectives that extend conditional flow matching to the operator setting with input-function-dependent couplings. To demonstrate the effectiveness of our approach, we present numerical experiments on a range of PDEs, including the 1D advection and Burgers' equation, and a 2D Darcy flow problem for flow through a porous medium. We show that the proposed method can accurately learn solution operators across different resolutions and fidelities and produces uncertainty estimates that appropriately reflect model confidence, even when trained on limited high-fidelity data.

Attention-Enhanced Convolutional Autoencoder and Structured Delay Embeddings for Weather Prediction

Weather prediction is a quintessential problem involving the forecasting of a complex, nonlinear, and chaotic high-dimensional dynamical system. This work introduces an efficient reduced-order modeling (ROM) framework for short-range weather prediction and investigates fundamental questions in dimensionality reduction and reduced order modeling of such systems. Unlike recent AI-driven models, which require extensive computational resources, our framework prioritizes efficiency while achieving reasonable accuracy. Specifically, a ResNet-based convolutional autoencoder augmented by block attention modules is developed to reduce the dimensionality of high-dimensional weather data. Subsequently, a linear operator is learned in the time-delayed embedding of the latent space to efficiently capture the dynamics. Using the ERA5 reanalysis dataset, we demonstrate that this framework performs well in-distribution as evidenced by effectively predicting weather patterns within training data periods. We also identify important limitations in generalizing to future states, particularly in maintaining prediction accuracy beyond the training window. Our analysis reveals that weather systems exhibit strong temporal correlations that can be effectively captured through linear operations in an appropriately constructed embedding space, and that projection error rather than inference error is the main bottleneck. These findings shed light on some key challenges in reduced-order modeling of chaotic systems and point toward opportunities for hybrid approaches that combine efficient reduced-order models as baselines with more sophisticated AI architectures, particularly for applications in long-term climate modeling where computational efficiency is paramount.

Active Inference AI Systems for Scientific Discovery

The rapid evolution of artificial intelligence has led to expectations of transformative scientific discovery, yet current systems remain fundamentally limited by their operational architectures, brittle reasoning mechanisms, and their separation from experimental reality. Building on earlier work, we contend that progress in AI-driven science now depends on closing three fundamental gaps -- the abstraction gap, the reasoning gap, and the reality gap -- rather than on model size/data/test time compute. Scientific reasoning demands internal representations that support simulation of actions and response, causal structures that distinguish correlation from mechanism, and continuous calibration. We define active inference AI systems for scientific discovery as those that (i) maintain long-lived research memories grounded in causal self-supervised foundation models, (ii) symbolic or neuro-symbolic planners equipped with Bayesian guardrails, (iii) grow persistent knowledge graphs where thinking generates novel conceptual nodes, reasoning establishes causal edges, and real-world interaction prunes false connections while strengthening verified pathways, and (iv) refine their internal representations through closed-loop interaction with both high-fidelity simulators and automated laboratories - an operational loop where mental simulation guides action and empirical surprise reshapes understanding. In essence, we outline an architecture where discovery arises from the interplay between internal models that enable counterfactual reasoning and external validation that grounds hypotheses in reality. It is also argued that the inherent ambiguity in feedback from simulations and experiments, and underlying uncertainties makes human judgment indispensable, not as a temporary scaffold but as a permanent architectural component.

LaDCast: A Latent Diffusion Model for Medium-Range Ensemble Weather Forecasting

Accurate probabilistic weather forecasting demands both high accuracy and efficient uncertainty quantification, challenges that overburden both ensemble numerical weather prediction (NWP) and recent machine-learning methods. We introduce LaDCast, the first global latent-diffusion framework for medium-range ensemble forecasting, which generates hourly ensemble forecasts entirely in a learned latent space. An autoencoder compresses high-dimensional ERA5 reanalysis fields into a compact representation, and a transformer-based diffusion model produces sequential latent updates with arbitrary hour initialization. The model incorporates Geometric Rotary Position Embedding (GeoRoPE) to account for the Earth's spherical geometry, a dual-stream attention mechanism for efficient conditioning, and sinusoidal temporal embeddings to capture seasonal patterns. LaDCast achieves deterministic and probabilistic skill close to that of the European Centre for Medium-Range Forecast IFS-ENS, without any explicit perturbations. Notably, LaDCast demonstrates superior performance in tracking rare extreme events such as cyclones, capturing their trajectories more accurately than established models. By operating in latent space, LaDCast reduces storage and compute by orders of magnitude, demonstrating a practical path toward forecasting at kilometer-scale resolution in real time. We open-source our code and models and provide the training and evaluation pipelines at: https://github.com/tonyzyl/ladcast.

Spatially-Aware Diffusion Models with Cross-Attention for Global Field Reconstruction with Sparse Observations

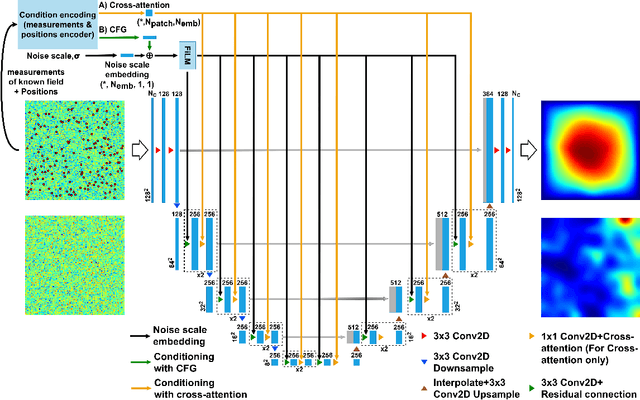
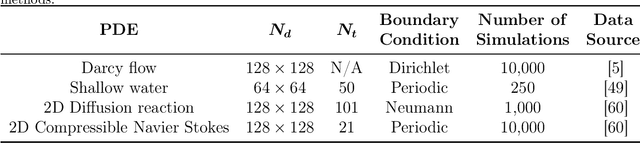
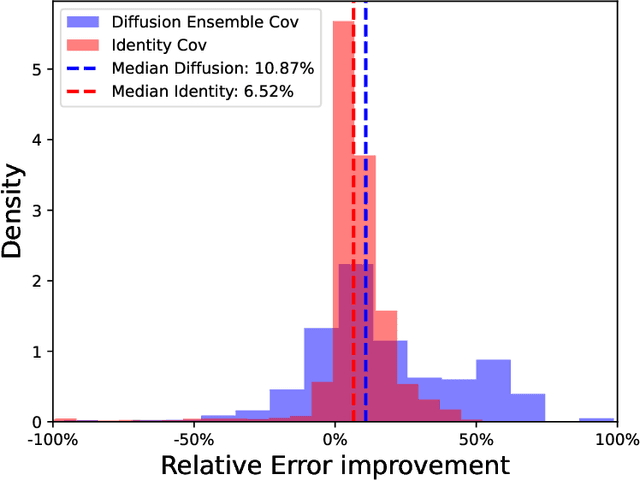
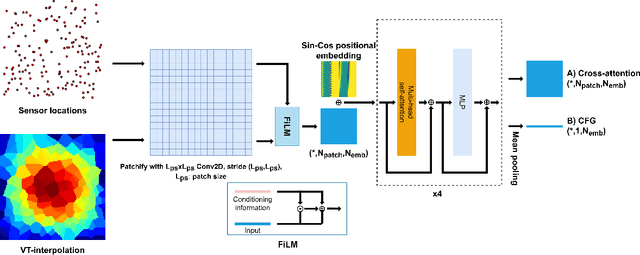
Diffusion models have gained attention for their ability to represent complex distributions and incorporate uncertainty, making them ideal for robust predictions in the presence of noisy or incomplete data. In this study, we develop and enhance score-based diffusion models in field reconstruction tasks, where the goal is to estimate complete spatial fields from partial observations. We introduce a condition encoding approach to construct a tractable mapping mapping between observed and unobserved regions using a learnable integration of sparse observations and interpolated fields as an inductive bias. With refined sensing representations and an unraveled temporal dimension, our method can handle arbitrary moving sensors and effectively reconstruct fields. Furthermore, we conduct a comprehensive benchmark of our approach against a deterministic interpolation-based method across various static and time-dependent PDEs. Our study attempts to addresses the gap in strong baselines for evaluating performance across varying sampling hyperparameters, noise levels, and conditioning methods. Our results show that diffusion models with cross-attention and the proposed conditional encoding generally outperform other methods under noisy conditions, although the deterministic method excels with noiseless data. Additionally, both the diffusion models and the deterministic method surpass the numerical approach in accuracy and computational cost for the steady problem. We also demonstrate the ability of the model to capture possible reconstructions and improve the accuracy of fused results in covariance-based correction tasks using ensemble sampling.

Enhancing Dynamical System Modeling through Interpretable Machine Learning Augmentations: A Case Study in Cathodic Electrophoretic Deposition

We introduce a comprehensive data-driven framework aimed at enhancing the modeling of physical systems, employing inference techniques and machine learning enhancements. As a demonstrative application, we pursue the modeling of cathodic electrophoretic deposition (EPD), commonly known as e-coating. Our approach illustrates a systematic procedure for enhancing physical models by identifying their limitations through inference on experimental data and introducing adaptable model enhancements to address these shortcomings. We begin by tackling the issue of model parameter identifiability, which reveals aspects of the model that require improvement. To address generalizability , we introduce modifications which also enhance identifiability. However, these modifications do not fully capture essential experimental behaviors. To overcome this limitation, we incorporate interpretable yet flexible augmentations into the baseline model. These augmentations are parameterized by simple fully-connected neural networks (FNNs), and we leverage machine learning tools, particularly Neural Ordinary Differential Equations (Neural ODEs), to learn these augmentations. Our simulations demonstrate that the machine learning-augmented model more accurately captures observed behaviors and improves predictive accuracy. Nevertheless, we contend that while the model updates offer superior performance and capture the relevant physics, we can reduce off-line computational costs by eliminating certain dynamics without compromising accuracy or interpretability in downstream predictions of quantities of interest, particularly film thickness predictions. The entire process outlined here provides a structured approach to leverage data-driven methods. Firstly, it helps us comprehend the root causes of model inaccuracies, and secondly, it offers a principled method for enhancing model performance.

CoCoGen: Physically-Consistent and Conditioned Score-based Generative Models for Forward and Inverse Problems

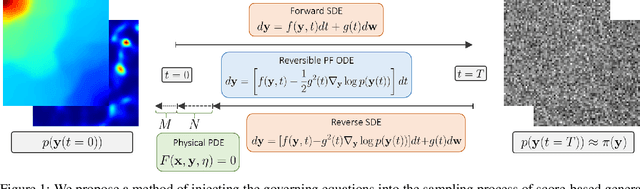
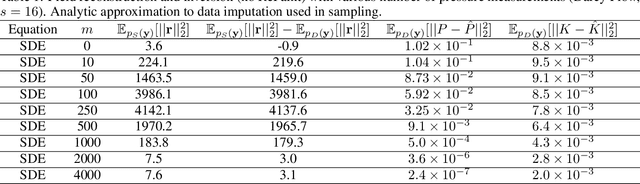
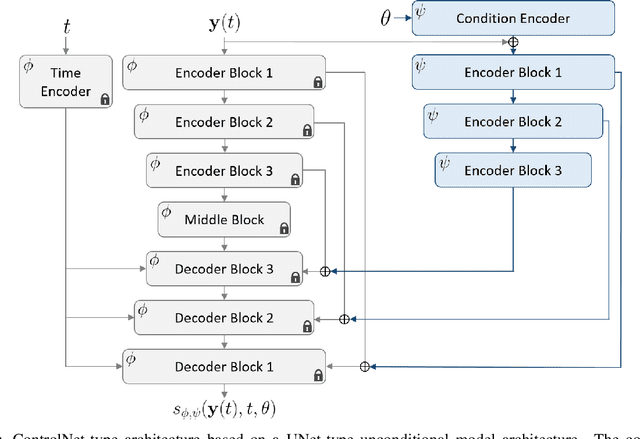
Recent advances in generative artificial intelligence have had a significant impact on diverse domains spanning computer vision, natural language processing, and drug discovery. This work extends the reach of generative models into physical problem domains, particularly addressing the efficient enforcement of physical laws and conditioning for forward and inverse problems involving partial differential equations (PDEs). Our work introduces two key contributions: firstly, we present an efficient approach to promote consistency with the underlying PDE. By incorporating discretized information into score-based generative models, our method generates samples closely aligned with the true data distribution, showcasing residuals comparable to data generated through conventional PDE solvers, significantly enhancing fidelity. Secondly, we showcase the potential and versatility of score-based generative models in various physics tasks, specifically highlighting surrogate modeling as well as probabilistic field reconstruction and inversion from sparse measurements. A robust foundation is laid by designing unconditional score-based generative models that utilize reversible probability flow ordinary differential equations. Leveraging conditional models that require minimal training, we illustrate their flexibility when combined with a frozen unconditional model. These conditional models generate PDE solutions by incorporating parameters, macroscopic quantities, or partial field measurements as guidance. The results illustrate the inherent flexibility of score-based generative models and explore the synergy between unconditional score-based generative models and the present physically-consistent sampling approach, emphasizing the power and flexibility in solving for and inverting physical fields governed by differential equations, and in other scientific machine learning tasks.

Easy attention: A simple self-attention mechanism for Transformers

To improve the robustness of transformer neural networks used for temporal-dynamics prediction of chaotic systems, we propose a novel attention mechanism called easy attention. Due to the fact that self attention only makes usage of the inner product of queries and keys, it is demonstrated that the keys, queries and softmax are not necessary for obtaining the attention score required to capture long-term dependencies in temporal sequences. Through implementing singular-value decomposition (SVD) on the softmax attention score, we further observe that the self attention compresses contribution from both queries and keys in the spanned space of the attention score. Therefore, our proposed easy-attention method directly treats the attention scores as learnable parameters. This approach produces excellent results when reconstructing and predicting the temporal dynamics of chaotic systems exhibiting more robustness and less complexity than the self attention or the widely-used long short-term memory (LSTM) network. Our results show great potential for applications in more complex high-dimensional dynamical systems.

On the lifting and reconstruction of dynamical systems with multiple attractors

The Koopman operator provides a linear perspective on non-linear dynamics by focusing on the evolution of observables in an invariant subspace. Observables of interest are typically linearly reconstructed from the Koopman eigenfunctions. Despite the broad use of Koopman operators over the past few years, there exist some misconceptions about the applicability of Koopman operators to dynamical systems with more than one fixed point. In this work, an explanation is provided for the mechanism of lifting for the Koopman operator of a dynamical system with multiple attractors. Considering the example of the Duffing oscillator, we show that by exploiting the inherent symmetry between the basins of attraction, a linear reconstruction with three degrees of freedom in the Koopman observable space is sufficient to globally linearize the system.

Conditionally Parameterized, Discretization-Aware Neural Networks for Mesh-Based Modeling of Physical Systems

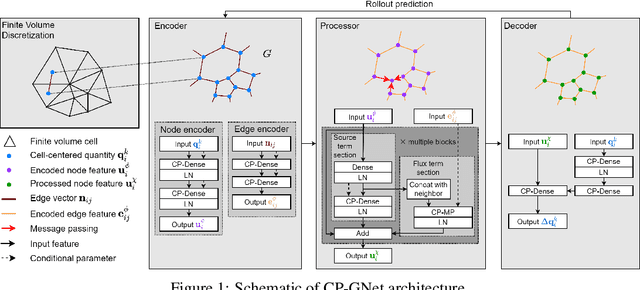
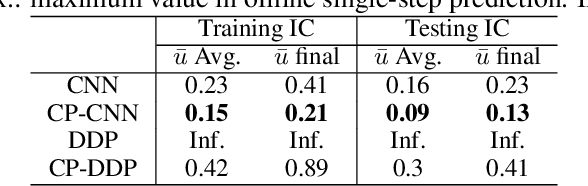
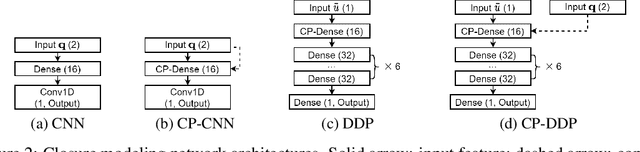
The numerical simulations of physical systems are heavily dependent on mesh-based models. While neural networks have been extensively explored to assist such tasks, they often ignore the interactions or hierarchical relations between input features, and process them as concatenated mixtures. In this work, we generalize the idea of conditional parametrization -- using trainable functions of input parameters to generate the weights of a neural network, and extend them in a flexible way to encode information critical to the numerical simulations. Inspired by discretized numerical methods, choices of the parameters include physical quantities and mesh topology features. The functional relation between the modeled features and the parameters are built into the network architecture. The method is implemented on different networks, which are applied to several frontier scientific machine learning tasks, including the discovery of unmodeled physics, super-resolution of coarse fields, and the simulation of unsteady flows with chemical reactions. The results show that the conditionally parameterized networks provide superior performance compared to their traditional counterparts. A network architecture named CP-GNet is also proposed as the first deep learning model capable of standalone prediction of reacting flows on irregular meshes.