Conditionally Parameterized, Discretization-Aware Neural Networks for Mesh-Based Modeling of Physical Systems
Paper and Code
Oct 08, 2021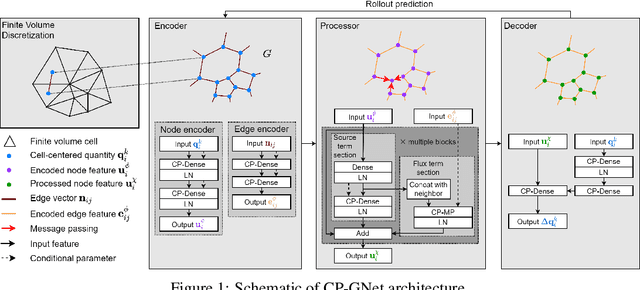
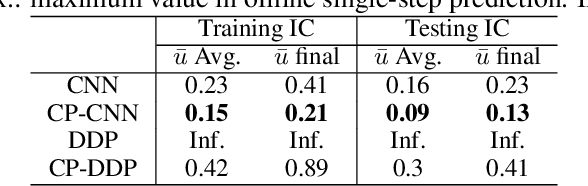
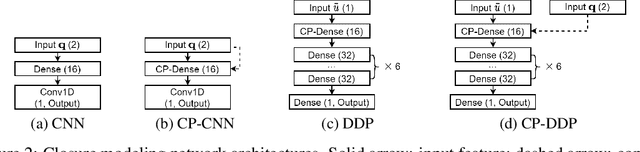

The numerical simulations of physical systems are heavily dependent on mesh-based models. While neural networks have been extensively explored to assist such tasks, they often ignore the interactions or hierarchical relations between input features, and process them as concatenated mixtures. In this work, we generalize the idea of conditional parametrization -- using trainable functions of input parameters to generate the weights of a neural network, and extend them in a flexible way to encode information critical to the numerical simulations. Inspired by discretized numerical methods, choices of the parameters include physical quantities and mesh topology features. The functional relation between the modeled features and the parameters are built into the network architecture. The method is implemented on different networks, which are applied to several frontier scientific machine learning tasks, including the discovery of unmodeled physics, super-resolution of coarse fields, and the simulation of unsteady flows with chemical reactions. The results show that the conditionally parameterized networks provide superior performance compared to their traditional counterparts. A network architecture named CP-GNet is also proposed as the first deep learning model capable of standalone prediction of reacting flows on irregular meshes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge