Deep Autoencoder with SVD-Like Convergence and Flat Minima

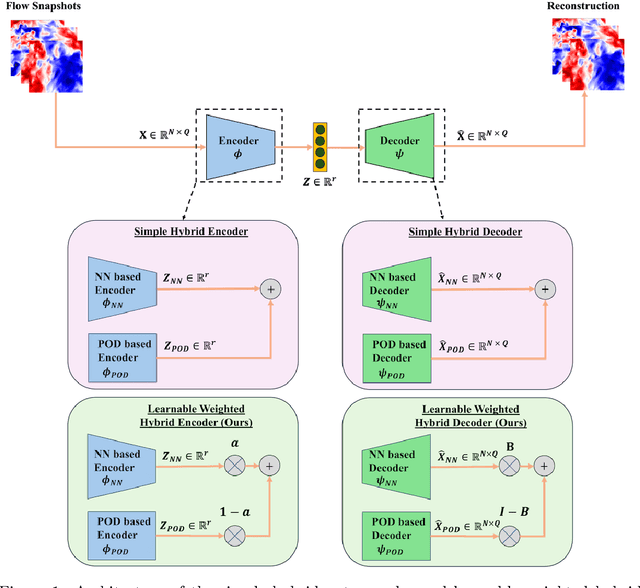
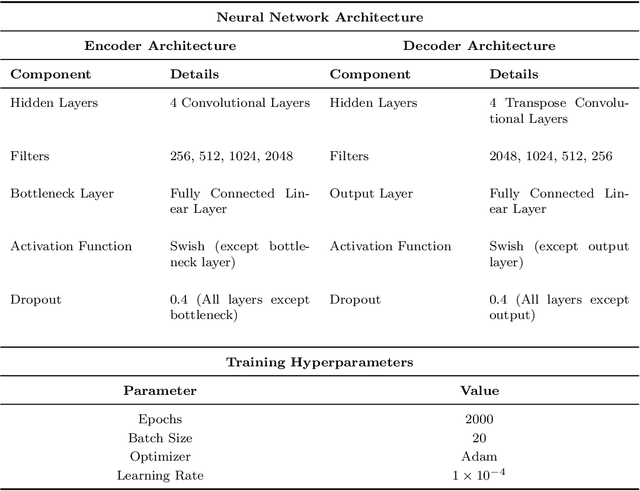
Representation learning for high-dimensional, complex physical systems aims to identify a low-dimensional intrinsic latent space, which is crucial for reduced-order modeling and modal analysis. To overcome the well-known Kolmogorov barrier, deep autoencoders (AEs) have been introduced in recent years, but they often suffer from poor convergence behavior as the rank of the latent space increases. To address this issue, we propose the learnable weighted hybrid autoencoder, a hybrid approach that combines the strengths of singular value decomposition (SVD) with deep autoencoders through a learnable weighted framework. We find that the introduction of learnable weighting parameters is essential - without them, the resulting model would either collapse into a standard POD or fail to exhibit the desired convergence behavior. Additionally, we empirically find that our trained model has a sharpness thousands of times smaller compared to other models. Our experiments on classical chaotic PDE systems, including the 1D Kuramoto-Sivashinsky and forced isotropic turbulence datasets, demonstrate that our approach significantly improves generalization performance compared to several competing methods, paving the way for robust representation learning of high-dimensional, complex physical systems.

Learning Noise-Robust Stable Koopman Operator for Control with Physics-Informed Observables

We propose a novel learning framework for Koopman operator of nonlinear dynamical systems that is informed by the governing equation and guarantees long-time stability and robustness to noise. In contrast to existing frameworks where either ad-hoc observables or blackbox neural networks are used to construct observables in the extended dynamic mode decomposition (EDMD), our observables are informed by governing equations via Polyflow. To improve the noise robustness and guarantee long-term stability, we designed a stable parameterization of the Koopman operator together with a progressive learning strategy for roll-out recurrent loss. To further improve model performance in the phase space, a simple iterative strategy of data augmentation was developed. Numerical experiments of prediction and control of classic nonlinear systems with ablation study showed the effectiveness of the proposed techniques over several state-of-the-art practices.

Grad-Shafranov equilibria via data-free physics informed neural networks

A large number of magnetohydrodynamic (MHD) equilibrium calculations are often required for uncertainty quantification, optimization, and real-time diagnostic information, making MHD equilibrium codes vital to the field of plasma physics. In this paper, we explore a method for solving the Grad-Shafranov equation by using Physics-Informed Neural Networks (PINNs). For PINNs, we optimize neural networks by directly minimizing the residual of the PDE as a loss function. We show that PINNs can accurately and effectively solve the Grad-Shafranov equation with several different boundary conditions. We also explore the parameter space by varying the size of the model, the learning rate, and boundary conditions to map various trade-offs such as between reconstruction error and computational speed. Additionally, we introduce a parameterized PINN framework, expanding the input space to include variables such as pressure, aspect ratio, elongation, and triangularity in order to handle a broader range of plasma scenarios within a single network. Parametrized PINNs could be used in future work to solve inverse problems such as shape optimization.

PyKoopman: A Python Package for Data-Driven Approximation of the Koopman Operator

PyKoopman is a Python package for the data-driven approximation of the Koopman operator associated with a dynamical system. The Koopman operator is a principled linear embedding of nonlinear dynamics and facilitates the prediction, estimation, and control of strongly nonlinear dynamics using linear systems theory. In particular, PyKoopman provides tools for data-driven system identification for unforced and actuated systems that build on the equation-free dynamic mode decomposition (DMD) and its variants. In this work, we provide a brief description of the mathematical underpinnings of the Koopman operator, an overview and demonstration of the features implemented in PyKoopman (with code examples), practical advice for users, and a list of potential extensions to PyKoopman. Software is available at http://github.com/dynamicslab/pykoopman

On the lifting and reconstruction of dynamical systems with multiple attractors

The Koopman operator provides a linear perspective on non-linear dynamics by focusing on the evolution of observables in an invariant subspace. Observables of interest are typically linearly reconstructed from the Koopman eigenfunctions. Despite the broad use of Koopman operators over the past few years, there exist some misconceptions about the applicability of Koopman operators to dynamical systems with more than one fixed point. In this work, an explanation is provided for the mechanism of lifting for the Koopman operator of a dynamical system with multiple attractors. Considering the example of the Duffing oscillator, we show that by exploiting the inherent symmetry between the basins of attraction, a linear reconstruction with three degrees of freedom in the Koopman observable space is sufficient to globally linearize the system.

Neural Implicit Flow: a mesh-agnostic dimensionality reduction paradigm of spatio-temporal data

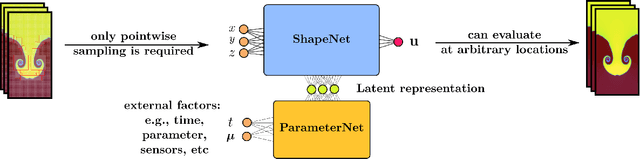
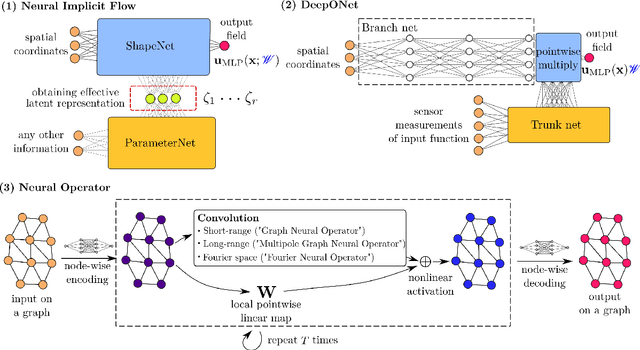
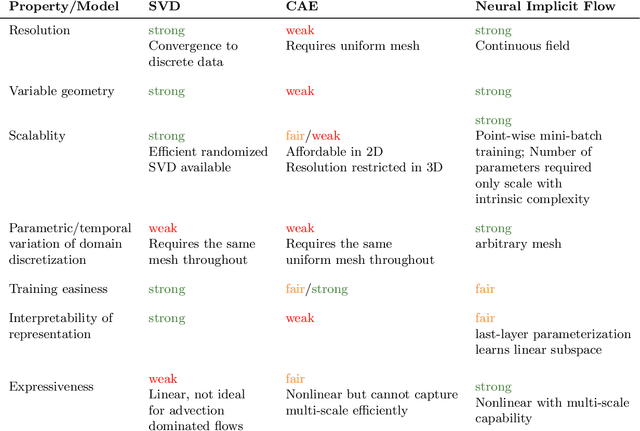
High-dimensional spatio-temporal dynamics can often be encoded in a low-dimensional subspace. Engineering applications for modeling, characterization, design, and control of such large-scale systems often rely on dimensionality reduction to make solutions computationally tractable in real-time. Common existing paradigms for dimensionality reduction include linear methods, such as the singular value decomposition (SVD), and nonlinear methods, such as variants of convolutional autoencoders (CAE). However, these encoding techniques lack the ability to efficiently represent the complexity associated with spatio-temporal data, which often requires variable geometry, non-uniform grid resolution, adaptive meshing, and/or parametric dependencies. To resolve these practical engineering challenges, we propose a general framework called Neural Implicit Flow (NIF) that enables a mesh-agnostic, low-rank representation of large-scale, parametric, spatial-temporal data. NIF consists of two modified multilayer perceptrons (MLPs): (i) ShapeNet, which isolates and represents the spatial complexity, and (ii) ParameterNet, which accounts for any other input complexity, including parametric dependencies, time, and sensor measurements. We demonstrate the utility of NIF for parametric surrogate modeling, enabling the interpretable representation and compression of complex spatio-temporal dynamics, efficient many-spatial-query tasks, and improved generalization performance for sparse reconstruction.

Non-linear Independent Dual System (NIDS) for Discretization-independent Surrogate Modeling over Complex Geometries

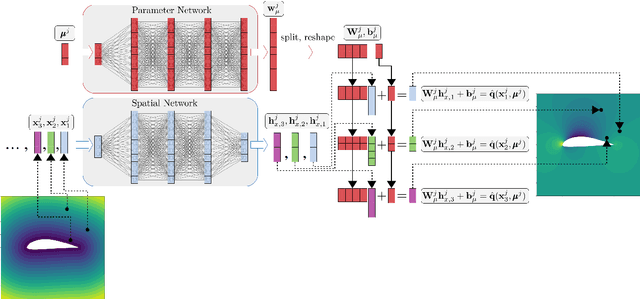
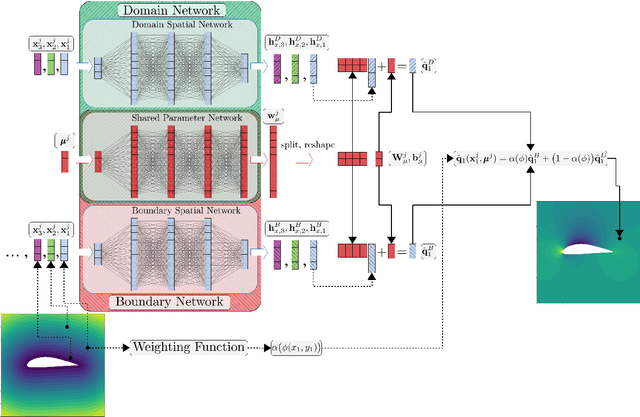
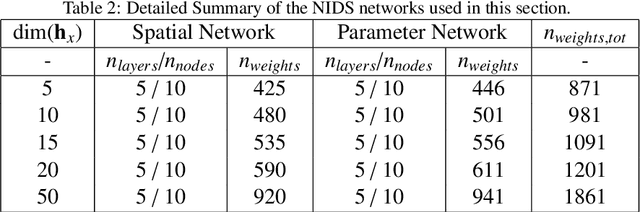
Numerical solutions of partial differential equations (PDEs) require expensive simulations, limiting their application in design optimization routines, model-based control, or solution of large-scale inverse problems. Existing Convolutional Neural Network-based frameworks for surrogate modeling require lossy pixelization and data-preprocessing, which is not suitable for realistic engineering applications. Therefore, we propose non-linear independent dual system (NIDS), which is a deep learning surrogate model for discretization-independent, continuous representation of PDE solutions, and can be used for prediction over domains with complex, variable geometries and mesh topologies. NIDS leverages implicit neural representations to develop a non-linear mapping between problem parameters and spatial coordinates to state predictions by combining evaluations of a case-wise parameter network and a point-wise spatial network in a linear output layer. The input features of the spatial network include physical coordinates augmented by a minimum distance function evaluation to implicitly encode the problem geometry. The form of the overall output layer induces a dual system, where each term in the map is non-linear and independent. Further, we propose a minimum distance function-driven weighted sum of NIDS models using a shared parameter network to enforce boundary conditions by construction under certain restrictions. The framework is applied to predict solutions around complex, parametrically-defined geometries on non-parametrically-defined meshes with solutions obtained many orders of magnitude faster than the full order models. Test cases include a vehicle aerodynamics problem with complex geometry and data scarcity, enabled by a training method in which more cases are gradually added as training progresses.

Sparsity-promoting algorithms for the discovery of informative Koopman invariant subspaces

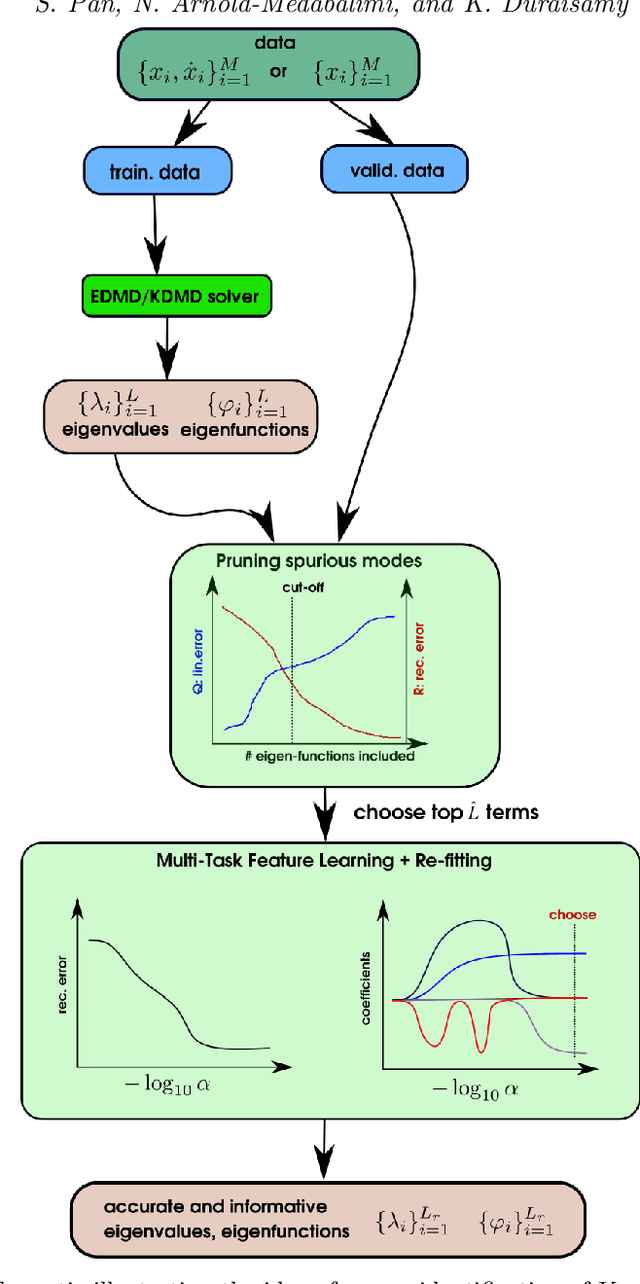
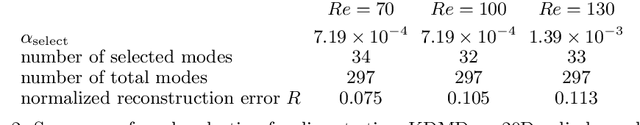
Koopman decomposition is a non-linear generalization of eigen decomposition, and is being increasingly utilized in the analysis of spatio-temporal dynamics. Well-known techniques such as the dynamic mode decomposition (DMD) and its variants provide approximations to the Koopman operator, and have been applied extensively in many fluid dynamic problems. Despite being endowed with a richer dictionary of nonlinear observables, nonlinear variants of the DMD, such as extended/kernel dynamic mode decomposition (EDMD/KDMD) are seldom applied to large-scale problems primarily due to the difficulty of discerning the Koopman invariant subspace from thousands of resulting Koopman triplets: eigenvalues, eigenvectors, and modes. To address this issue, we revisit the formulation of EDMD and KDMD, and propose an algorithm based on multi-task feature learning to extract the most informative Koopman invariant subspace by removing redundant and spurious Koopman triplets. These algorithms can be viewed as sparsity promoting extensions of EDMD/KDMD and are presented in an open-source package. Further, we extend KDMD to a continuous-time setting and show a relationship between the present algorithm, sparsity-promoting DMD and an empirical criterion from the viewpoint of non-convex optimization. The effectiveness of our algorithm is demonstrated on examples ranging from simple dynamical systems to two-dimensional cylinder wake flows at different Reynolds numbers and a three-dimensional turbulent ship air-wake flow. The latter two problems are designed such that very strong transients are present in the flow evolution, thus requiring accurate representation of decaying modes.

Particle reconstruction of volumetric particle image velocimetry with strategy of machine learning

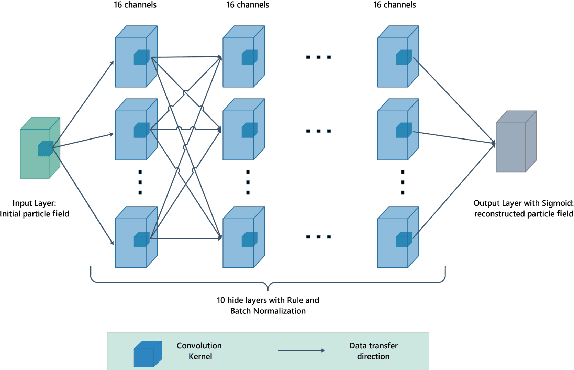
Three-dimensional particle reconstruction with limited two-dimensional projects is an underdetermined inverse problem that the exact solution is often difficulty to be obtained. In general, approximate solutions can be obtained by optimization methods. In the current work, a practical particle reconstruction method based on convolutional neural network (CNN) is proposed. The proposed technique can refine the particle reconstruction from a very coarse initial guess of particle distribution from any traditional algebraic reconstruction technique (ART) based methods. Compared with available ART-based algorithms, the novel technique makes significant improvements in terms of reconstruction quality and at least an order of magnitude faster with dense particle concentration.

Physics-Informed Probabilistic Learning of Linear Embeddings of Non-linear Dynamics With Guaranteed Stability

The Koopman operator has emerged as a powerful tool for the analysis of nonlinear dynamical systems as it provides coordinate transformations which can globally linearize the dynamics. Recent deep learning approaches such as Linearly-Recurrent Autoencoder Networks (LRAN) show great promise for discovering the Koopman operator for a general nonlinear dynamical system from a data-driven perspective, but several challenges remain. In this work, we formalize the problem of learning the continuous-time Koopman operator with deep neural nets in a measure-theoretic framework. This induces two forms of models: differential and recurrent form, the choice of which depends on the availability of the governing equation and data. We then enforce a structural parameterization that renders the realization of the Koopman operator provably stable. A new autoencoder architecture is constructed, such that only the residual of the dynamic mode decomposition is learned. Finally, we employ mean-field variational inference (MFVI) on the aforementioned framework in a hierarchical Bayesian setting to quantify uncertainties in the characterization and prediction of the dynamics of observables. The framework is evaluated on a simple polynomial system, the Duffing oscillator, and an unstable cylinder wake flow with noisy measurements.