PyKoopman: A Python Package for Data-Driven Approximation of the Koopman Operator

PyKoopman is a Python package for the data-driven approximation of the Koopman operator associated with a dynamical system. The Koopman operator is a principled linear embedding of nonlinear dynamics and facilitates the prediction, estimation, and control of strongly nonlinear dynamics using linear systems theory. In particular, PyKoopman provides tools for data-driven system identification for unforced and actuated systems that build on the equation-free dynamic mode decomposition (DMD) and its variants. In this work, we provide a brief description of the mathematical underpinnings of the Koopman operator, an overview and demonstration of the features implemented in PyKoopman (with code examples), practical advice for users, and a list of potential extensions to PyKoopman. Software is available at http://github.com/dynamicslab/pykoopman

Modern Koopman Theory for Dynamical Systems

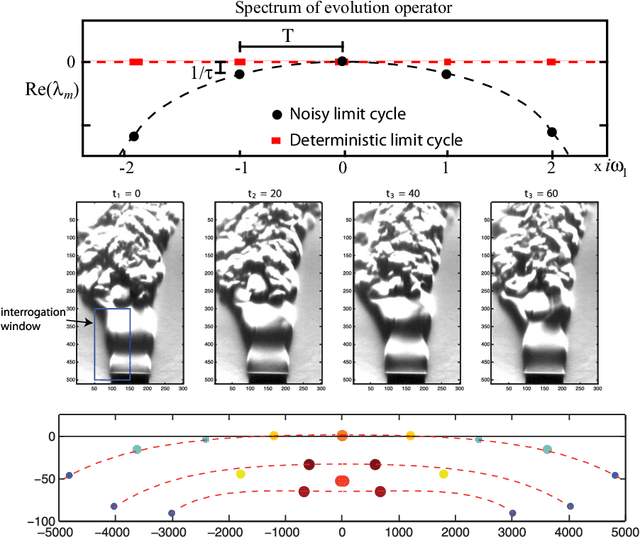
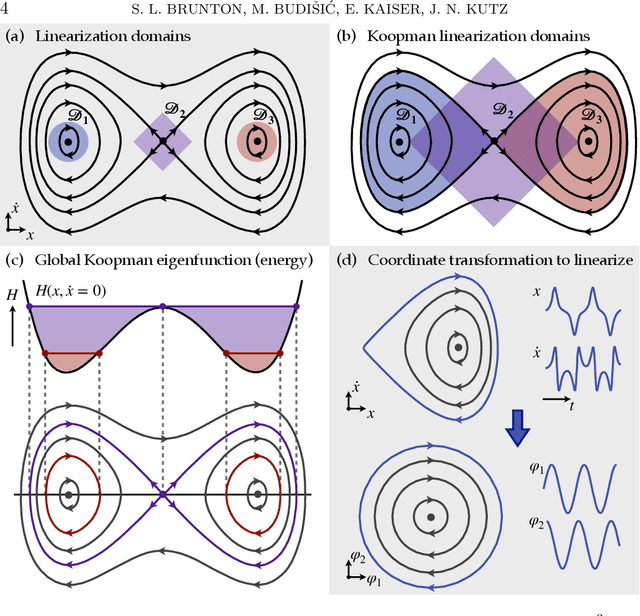
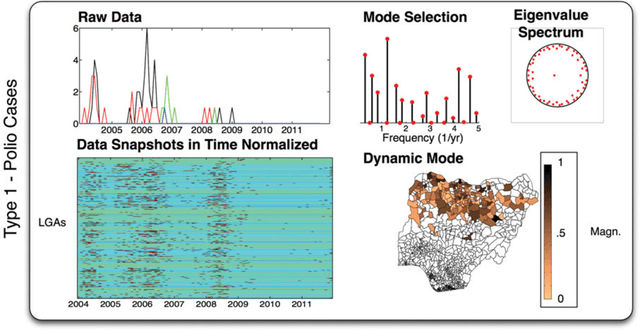
The field of dynamical systems is being transformed by the mathematical tools and algorithms emerging from modern computing and data science. First-principles derivations and asymptotic reductions are giving way to data-driven approaches that formulate models in operator theoretic or probabilistic frameworks. Koopman spectral theory has emerged as a dominant perspective over the past decade, in which nonlinear dynamics are represented in terms of an infinite-dimensional linear operator acting on the space of all possible measurement functions of the system. This linear representation of nonlinear dynamics has tremendous potential to enable the prediction, estimation, and control of nonlinear systems with standard textbook methods developed for linear systems. However, obtaining finite-dimensional coordinate systems and embeddings in which the dynamics appear approximately linear remains a central open challenge. The success of Koopman analysis is due primarily to three key factors: 1) there exists rigorous theory connecting it to classical geometric approaches for dynamical systems, 2) the approach is formulated in terms of measurements, making it ideal for leveraging big-data and machine learning techniques, and 3) simple, yet powerful numerical algorithms, such as the dynamic mode decomposition (DMD), have been developed and extended to reduce Koopman theory to practice in real-world applications. In this review, we provide an overview of modern Koopman operator theory, describing recent theoretical and algorithmic developments and highlighting these methods with a diverse range of applications. We also discuss key advances and challenges in the rapidly growing field of machine learning that are likely to drive future developments and significantly transform the theoretical landscape of dynamical systems.

Learning Discrepancy Models From Experimental Data

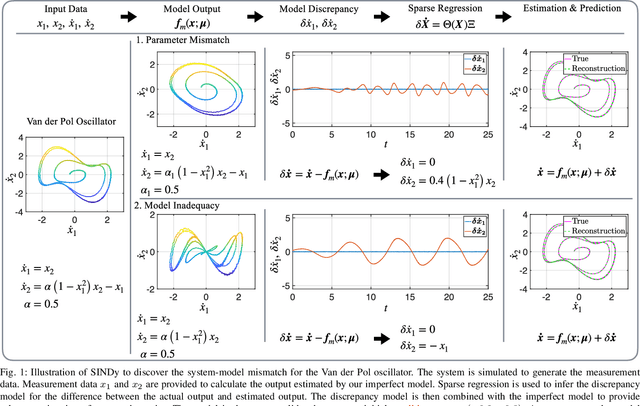
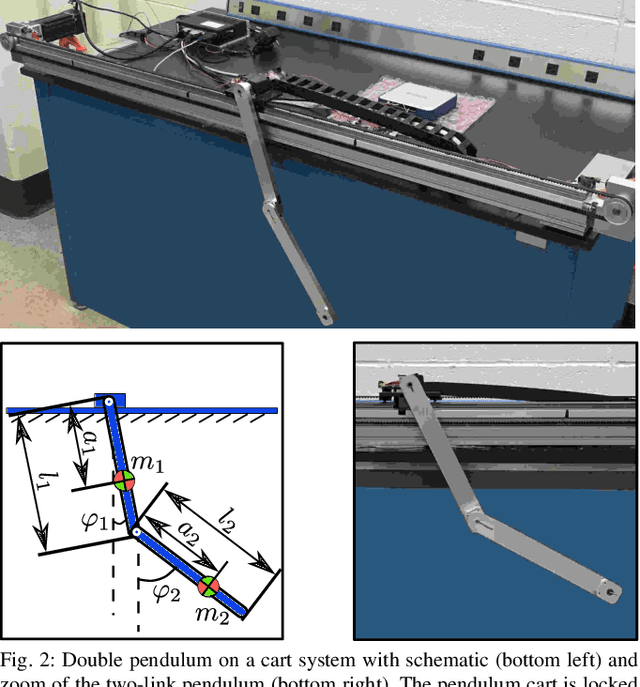
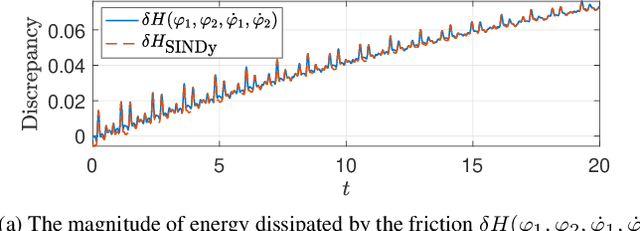
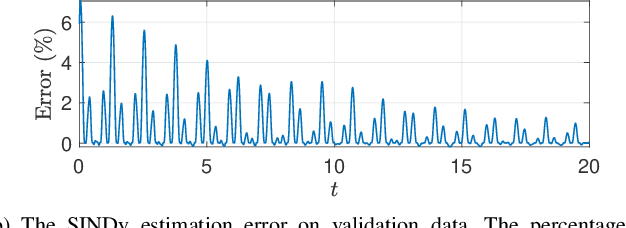
First principles modeling of physical systems has led to significant technological advances across all branches of science. For nonlinear systems, however, small modeling errors can lead to significant deviations from the true, measured behavior. Even in mechanical systems, where the equations are assumed to be well-known, there are often model discrepancies corresponding to nonlinear friction, wind resistance, etc. Discovering models for these discrepancies remains an open challenge for many complex systems. In this work, we use the sparse identification of nonlinear dynamics (SINDy) algorithm to discover a model for the discrepancy between a simplified model and measurement data. In particular, we assume that the model mismatch can be sparsely represented in a library of candidate model terms. We demonstrate the efficacy of our approach on several examples including experimental data from a double pendulum on a cart. We further design and implement a feed-forward controller in simulations, showing improvement with a discrepancy model.

Discovering conservation laws from data for control

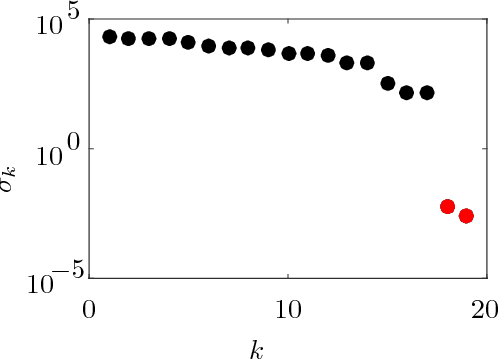
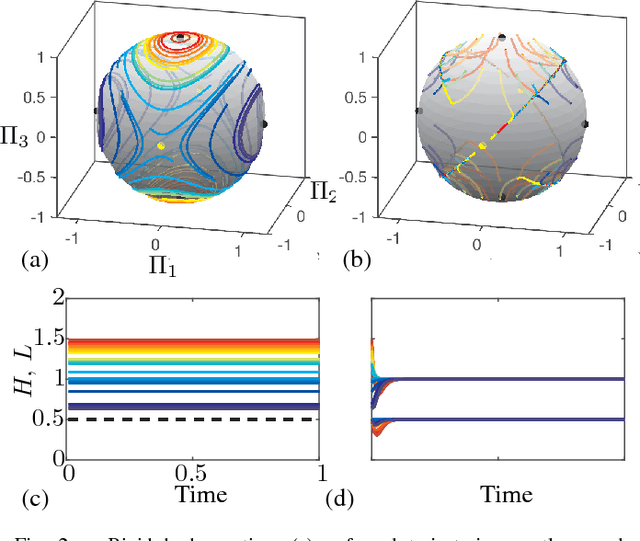
Conserved quantities, i.e. constants of motion, are critical for characterizing many dynamical systems in science and engineering. These quantities are related to underlying symmetries and they provide fundamental knowledge about physical laws, describe the evolution of the system, and enable system reduction. In this work, we formulate a data-driven architecture for discovering conserved quantities based on Koopman theory. The Koopman operator has emerged as a principled linear embedding of nonlinear dynamics, and its eigenfunctions establish intrinsic coordinates along which the dynamics behave linearly. Interestingly, eigenfunctions of the Koopman operator associated with vanishing eigenvalues correspond to conserved quantities of the underlying system. In this paper, we show that these invariants may be identified with data-driven regression and power series expansions, based on the infinitesimal generator of the Koopman operator. We further establish a connection between the Koopman framework, conserved quantities, and the Lie-Poisson bracket. This data-driven method for discovering conserved quantities is demonstrated on the three-dimensional rigid body equations, where we simultaneously discover the total energy and angular momentum and use these intrinsic coordinates to develop a model predictive controller to track a given reference value.