Modeling and LQR Control of Insect Sized Flapping Wing Robot

Flying insects can perform rapid, sophisticated maneuvers like backflips, sharp banked turns, and in-flight collision recovery. To emulate these in aerial robots weighing less than a gram, known as flying insect robots (FIRs), a fast and responsive control system is essential. To date, these have largely been, at their core, elaborations of proportional-integral-derivative (PID)-type feedback control. Without exception, their gains have been painstakingly tuned by hand. Aggressive maneuvers have further required task-specific tuning. Optimal control has the potential to mitigate these issues, but has to date only been demonstrated using approxiate models and receding horizon controllers (RHC) that are too computationally demanding to be carried out onboard the robot. Here we used a more accurate stroke-averaged model of forces and torques to implement the first demonstration of optimal control on an FIR that is computationally efficient enough to be performed by a microprocessor carried onboard. We took force and torque measurements from a 150 mg FIR, the UW Robofly, using a custom-built sensitive force-torque sensor, and validated them using motion capture data in free flight. We demonstrated stable hovering (RMS error of about 4 cm) and trajectory tracking maneuvers at translational velocities up to 25 cm/s using an optimal linear quadratic regulator (LQR). These results were enabled by a more accurate model and lay the foundation for future work that uses our improved model and optimal controller in conjunction with recent advances in low-power receding horizon control to perform accurate aggressive maneuvers without iterative, task-specific tuning.

The Experimental Multi-Arm Pendulum on a Cart: A Benchmark System for Chaos, Learning, and Control

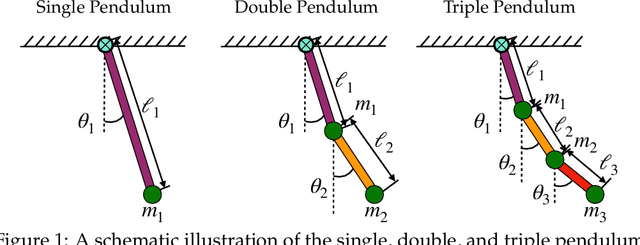
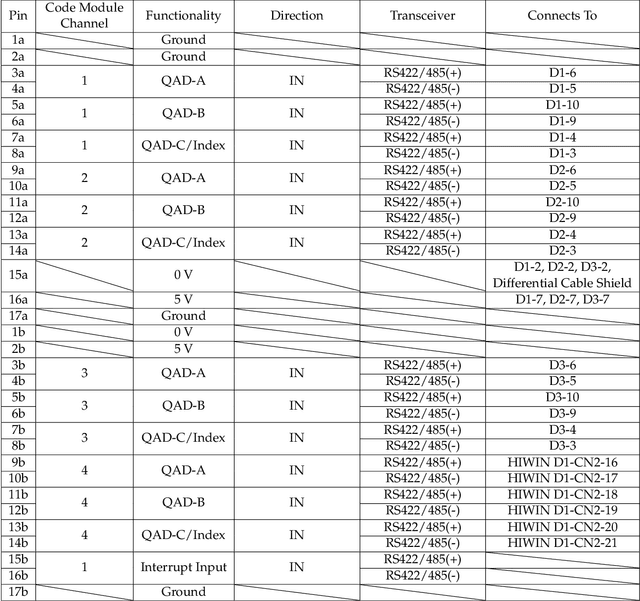
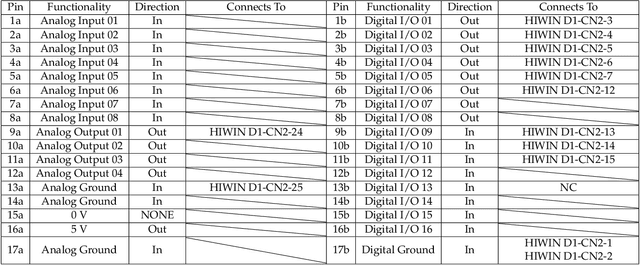
The single, double, and triple pendulum has served as an illustrative experimental benchmark system for scientists to study dynamical behavior for more than four centuries. The pendulum system exhibits a wide range of interesting behaviors, from simple harmonic motion in the single pendulum to chaotic dynamics in multi-arm pendulums. Under forcing, even the single pendulum may exhibit chaos, providing a simple example of a damped-driven system. All multi-armed pendulums are characterized by the existence of index-one saddle points, which mediate the transport of trajectories in the system, providing a simple mechanical analog of various complex transport phenomena, from biolocomotion to transport within the solar system. Further, pendulum systems have long been used to design and test both linear and nonlinear control strategies, with the addition of more arms making the problem more challenging. In this work, we provide extensive designs for the construction and operation of a high-performance, multi-link pendulum on a cart system. Although many experimental setups have been built to study the behavior of pendulum systems, such an extensive documentation on the design, construction, and operation is missing from the literature. The resulting experimental system is highly flexible, enabling a wide range of benchmark problems in dynamical systems modeling, system identification and learning, and control. To promote reproducible research, we have made our entire system open-source, including 3D CAD drawings, basic tutorial code, and data. Moreover, we discuss the possibility of extending our system capability to be operated remotely to enable researchers all around the world to use it, thus increasing access.

PySINDy: A comprehensive Python package for robust sparse system identification

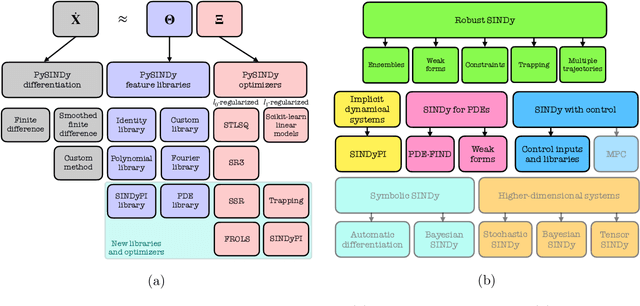
Automated data-driven modeling, the process of directly discovering the governing equations of a system from data, is increasingly being used across the scientific community. PySINDy is a Python package that provides tools for applying the sparse identification of nonlinear dynamics (SINDy) approach to data-driven model discovery. In this major update to PySINDy, we implement several advanced features that enable the discovery of more general differential equations from noisy and limited data. The library of candidate terms is extended for the identification of actuated systems, partial differential equations (PDEs), and implicit differential equations. Robust formulations, including the integral form of SINDy and ensembling techniques, are also implemented to improve performance for real-world data. Finally, we provide a range of new optimization algorithms, including several sparse regression techniques and algorithms to enforce and promote inequality constraints and stability. Together, these updates enable entirely new SINDy model discovery capabilities that have not been reported in the literature, such as constrained PDE identification and ensembling with different sparse regression optimizers.

Automatic Differentiation to Simultaneously Identify Nonlinear Dynamics and Extract Noise Probability Distributions from Data

The sparse identification of nonlinear dynamics (SINDy) is a regression framework for the discovery of parsimonious dynamic models and governing equations from time-series data. As with all system identification methods, noisy measurements compromise the accuracy and robustness of the model discovery procedure. In this work, we develop a variant of the SINDy algorithm that integrates automatic differentiation and recent time-stepping constrained motivated by Rudy et al. for simultaneously (i) denoising the data, (ii) learning and parametrizing the noise probability distribution, and (iii) identifying the underlying parsimonious dynamical system responsible for generating the time-series data. Thus within an integrated optimization framework, noise can be separated from signal, resulting in an architecture that is approximately twice as robust to noise as state-of-the-art methods, handling as much as 40% noise on a given time-series signal and explicitly parametrizing the noise probability distribution. We demonstrate this approach on several numerical examples, from Lotka-Volterra models to the spatio-temporal Lorenz 96 model. Further, we show the method can identify a diversity of probability distributions including Gaussian, uniform, Gamma, and Rayleigh.

SINDy-PI: A Robust Algorithm for Parallel Implicit Sparse Identification of Nonlinear Dynamics

Accurately modeling the nonlinear dynamics of a system from measurement data is a challenging yet vital topic. The sparse identification of nonlinear dynamics (SINDy) algorithm is one approach to discover dynamical systems models from data. Although extensions have been developed to identify implicit dynamics, or dynamics described by rational functions, these extensions are extremely sensitive to noise. In this work, we develop SINDy-PI (parallel, implicit), a robust variant of the SINDy algorithm to identify implicit dynamics and rational nonlinearities. The SINDy-PI framework includes multiple optimization algorithms and a principled approach to model selection. We demonstrate the ability of this algorithm to learn implicit ordinary and partial differential equations and conservation laws from limited and noisy data. In particular, we show that the proposed approach is several orders of magnitude more noise robust than previous approaches, and may be used to identify a class of complex ODE and PDE dynamics that were previously unattainable with SINDy, including for the double pendulum dynamics and the Belousov Zhabotinsky (BZ) reaction.

Learning Discrepancy Models From Experimental Data

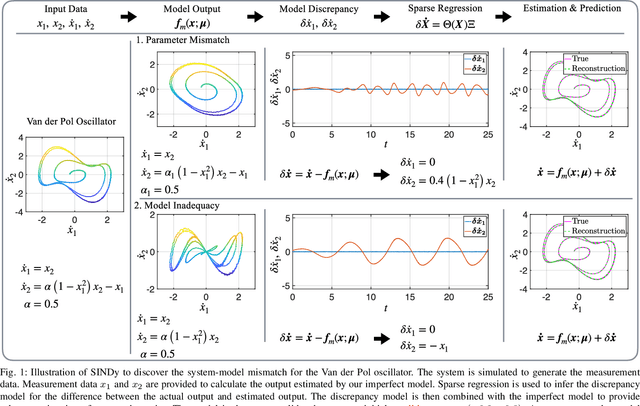
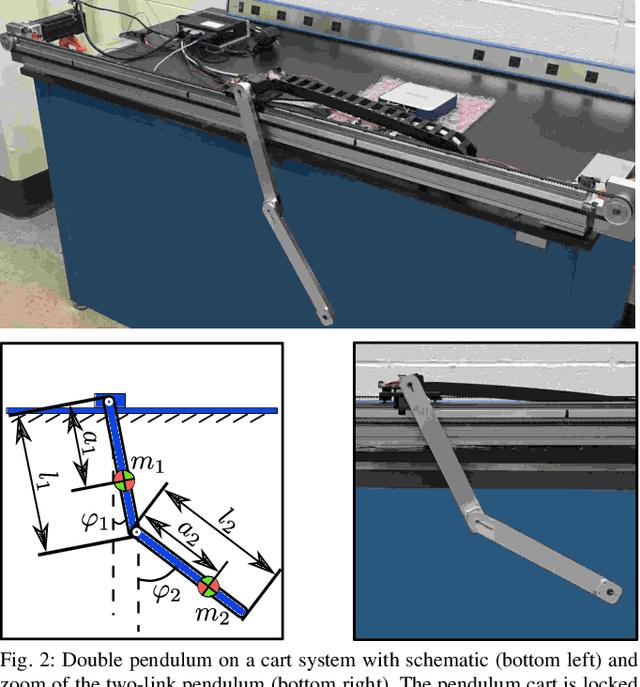
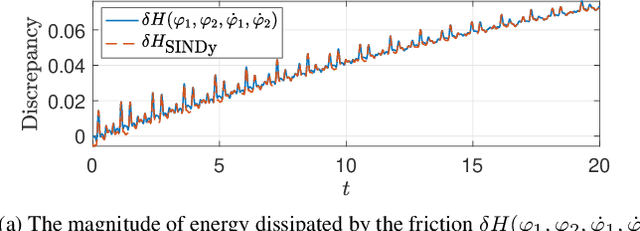
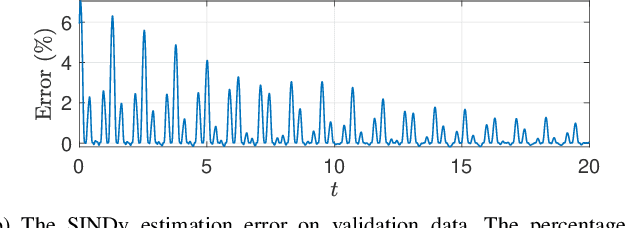
First principles modeling of physical systems has led to significant technological advances across all branches of science. For nonlinear systems, however, small modeling errors can lead to significant deviations from the true, measured behavior. Even in mechanical systems, where the equations are assumed to be well-known, there are often model discrepancies corresponding to nonlinear friction, wind resistance, etc. Discovering models for these discrepancies remains an open challenge for many complex systems. In this work, we use the sparse identification of nonlinear dynamics (SINDy) algorithm to discover a model for the discrepancy between a simplified model and measurement data. In particular, we assume that the model mismatch can be sparsely represented in a library of candidate model terms. We demonstrate the efficacy of our approach on several examples including experimental data from a double pendulum on a cart. We further design and implement a feed-forward controller in simulations, showing improvement with a discrepancy model.