Driving down Poisson error can offset classification error in clinical tasks

Medical machine learning algorithms are typically evaluated based on accuracy vs. a clinician-defined ground truth, a reasonable choice because trained clinicians are usually better classifiers than ML models. However, this metric does not fully reflect the clinical task: it neglects the fact that humans, even with perfect accuracy, are subject to sometimes significant error from the Poisson statistics of rare events, because clinical protocols often specify that a relatively small sample be examined. For example, to quantitate malaria on a thin blood film a clinician examines only 2000 red blood cells (0.0004 uL), which can yield large variation in actual number of parasites present due to Poisson variability, so that a perfect human's count can differ substantially from the true average load. In contrast, ML systems may be less accurate on an object level, but they also may have the option to examine more blood (e.g. 0.1 uL, or 250x). So while their accuracy as to parasite count in a particular sample is lower, the Poisson variability of their estimate is also lower due to larger sample size. Crucially, when an ML system moves out of the proof-of-concept stage and targets deployment in a clinical setting, its performance must match current standard of care. To this end, it may have the option to offset its lower accuracy by increasing sample size to reduce Poisson error, and thus attain the same net clinical performance as a perfectly accurate human limited by smaller sample size. In this paper, we analyze the mathematics of the trade-off between these two types of error, to enable teams developing ML systems to leverage a relative strength (larger sample sizes) to offset a relative weakness (classification accuracy). We illustrate the methods with two concrete examples: diagnosis and quantitation of malaria on blood films.

Use case-focused metrics to evaluate machine learning for diseases involving parasite loads

Communal hill-climbing, via comparison of algorithm performances, can greatly accelerate ML research. However, it requires task-relevant metrics. For diseases involving parasite loads, e.g., malaria and neglected tropical diseases (NTDs) such as schistosomiasis, the metrics currently reported in ML papers (e.g., AUC, F1 score) are ill-suited to the clinical task. As a result, the hill-climbing system is not enabling progress towards solutions that address these dire illnesses. Drawing on examples from malaria and NTDs, this paper highlights two gaps in current ML practice and proposes methods for improvement: (i) We describe aspects of ML development, and performance metrics in particular, that need to be firmly grounded in the clinical use case, and we offer methods for acquiring this domain knowledge. (ii) We describe in detail performance metrics to guide development of ML models for diseases involving parasite loads. We highlight the importance of a patient-level perspective, interpatient variability, false positive rates, limit of detection, and different types of error. We also discuss problems with ROC curves and AUC as commonly used in this context.

PySINDy: A comprehensive Python package for robust sparse system identification

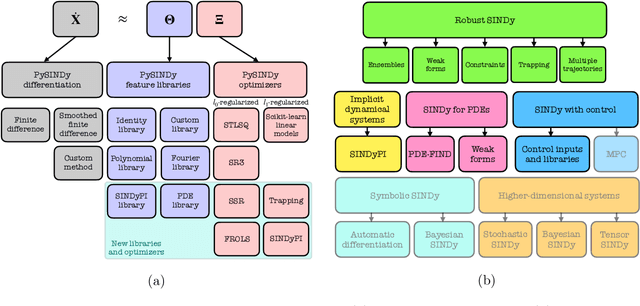
Automated data-driven modeling, the process of directly discovering the governing equations of a system from data, is increasingly being used across the scientific community. PySINDy is a Python package that provides tools for applying the sparse identification of nonlinear dynamics (SINDy) approach to data-driven model discovery. In this major update to PySINDy, we implement several advanced features that enable the discovery of more general differential equations from noisy and limited data. The library of candidate terms is extended for the identification of actuated systems, partial differential equations (PDEs), and implicit differential equations. Robust formulations, including the integral form of SINDy and ensembling techniques, are also implemented to improve performance for real-world data. Finally, we provide a range of new optimization algorithms, including several sparse regression techniques and algorithms to enforce and promote inequality constraints and stability. Together, these updates enable entirely new SINDy model discovery capabilities that have not been reported in the literature, such as constrained PDE identification and ensembling with different sparse regression optimizers.

A toolkit for data-driven discovery of governing equations in high-noise regimes

We consider the data-driven discovery of governing equations from time-series data in the limit of high noise. The algorithms developed describe an extensive toolkit of methods for circumventing the deleterious effects of noise in the context of the sparse identification of nonlinear dynamics (SINDy) framework. We offer two primary contributions, both focused on noisy data acquired from a system x' = f(x). First, we propose, for use in high-noise settings, an extensive toolkit of critically enabling extensions for the SINDy regression method, to progressively cull functionals from an over-complete library and yield a set of sparse equations that regress to the derivate x'. These innovations can extract sparse governing equations and coefficients from high-noise time-series data (e.g. 300% added noise). For example, it discovers the correct sparse libraries in the Lorenz system, with median coefficient estimate errors equal to 1% - 3% (for 50% noise), 6% - 8% (for 100% noise); and 23% - 25% (for 300% noise). The enabling modules in the toolkit are combined into a single method, but the individual modules can be tactically applied in other equation discovery methods (SINDy or not) to improve results on high-noise data. Second, we propose a technique, applicable to any model discovery method based on x' = f(x), to assess the accuracy of a discovered model in the context of non-unique solutions due to noisy data. Currently, this non-uniqueness can obscure a discovered model's accuracy and thus a discovery method's effectiveness. We describe a technique that uses linear dependencies among functionals to transform a discovered model into an equivalent form that is closest to the true model, enabling more accurate assessment of a discovered model's accuracy.

Fully-automated patient-level malaria assessment on field-prepared thin blood film microscopy images, including Supplementary Information

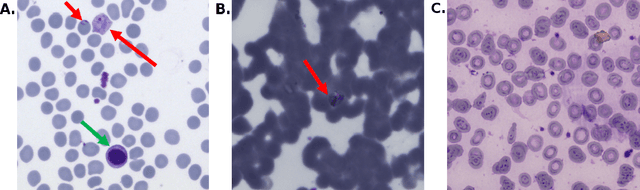
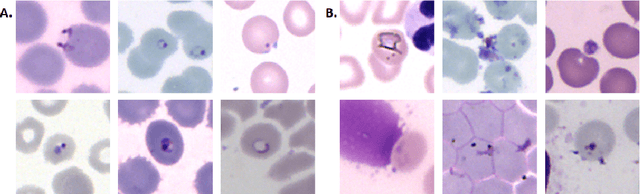
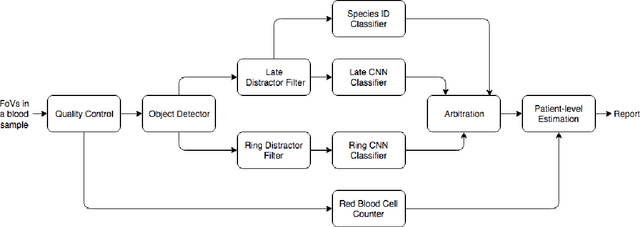
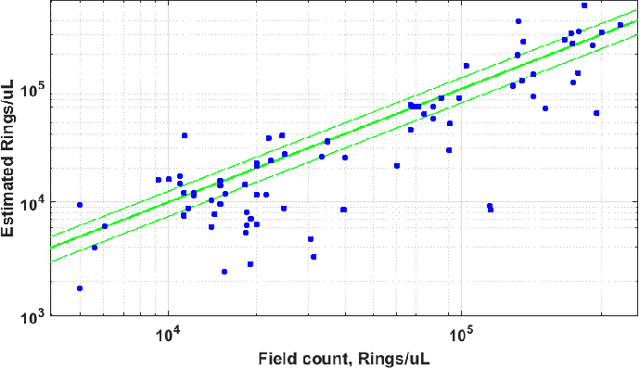
Malaria is a life-threatening disease affecting millions. Microscopy-based assessment of thin blood films is a standard method to (i) determine malaria species and (ii) quantitate high-parasitemia infections. Full automation of malaria microscopy by machine learning (ML) is a challenging task because field-prepared slides vary widely in quality and presentation, and artifacts often heavily outnumber relatively rare parasites. In this work, we describe a complete, fully-automated framework for thin film malaria analysis that applies ML methods, including convolutional neural nets (CNNs), trained on a large and diverse dataset of field-prepared thin blood films. Quantitation and species identification results are close to sufficiently accurate for the concrete needs of drug resistance monitoring and clinical use-cases on field-prepared samples. We focus our methods and our performance metrics on the field use-case requirements. We discuss key issues and important metrics for the application of ML methods to malaria microscopy.

Money on the Table: Statistical information ignored by Softmax can improve classifier accuracy

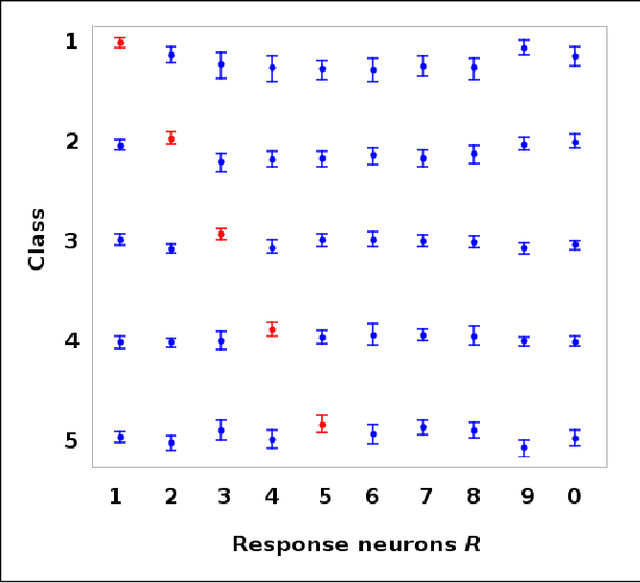
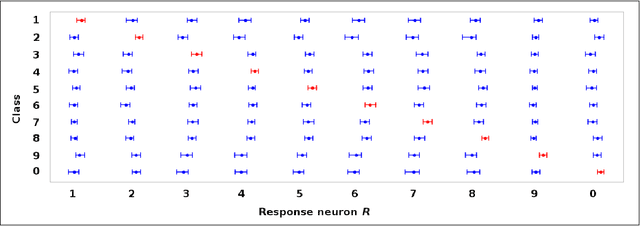
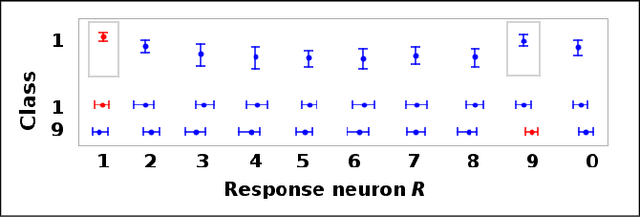
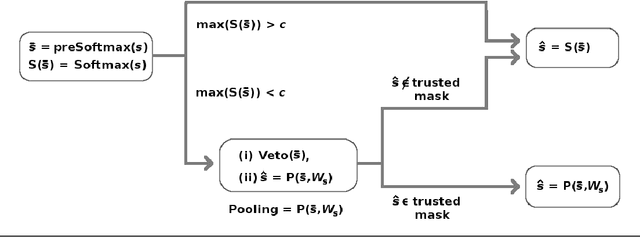
Softmax is a standard final layer used in Neural Nets (NNs) to summarize information encoded in the trained NN and return a prediction. However, Softmax leverages only a subset of the class-specific structure encoded in the trained model and ignores potentially valuable information: During training, models encode an array $D$ of class response distributions, where $D_{ij}$ is the distribution of the $j^{th}$ pre-Softmax readout neuron's responses to the $i^{th}$ class. Given a test sample, Softmax implicitly uses only the row of this array $D$ that corresponds to the readout neurons' responses to the sample's true class. Leveraging more of this array $D$ can improve classifier accuracy, because the likelihoods of two competing classes can be encoded in other rows of $D$. To explore this potential resource, we develop a hybrid classifier (Softmax-Pooling Hybrid, $SPH$) that uses Softmax on high-scoring samples, but on low-scoring samples uses a log-likelihood method that pools the information from the full array $D$. We apply $SPH$ to models trained on a vectorized MNIST dataset to varying levels of accuracy. $SPH$ replaces only the final Softmax layer in the trained NN, at test time only. All training is the same as for Softmax. Because the pooling classifier performs better than Softmax on low-scoring samples, $SPH$ reduces test set error by 6% to 23%, using the exact same trained model, whatever the baseline Softmax accuracy. This reduction in error reflects hidden capacity of the trained NN that is left unused by Softmax.

Putting a bug in ML: The moth olfactory network learns to read MNIST

We seek to (i) characterize the learning architectures exploited in biological neural networks for training on very few samples, and (ii) port these algorithmic structures to a machine learning context. The Moth Olfactory Network is among the simplest biological neural systems that can learn, and its architecture includes key structural elements widespread in biological neural nets, such as cascaded networks, competitive inhibition, high intrinsic noise, sparsity, reward mechanisms, and Hebbian plasticity. The interactions of these structural elements play a critical enabling role in rapid learning. We assign a computational model of the Moth Olfactory Network the task of learning to read the MNIST digits. This model, MothNet, is closely aligned with the moth's known biophysics and with in vivo electrode data, including data collected from moths learning new odors. We show that MothNet successfully learns to read given very few training samples (1 to 20 samples per class). In this few-samples regime, it substantially outperforms standard machine learning methods such as nearest-neighbors, support-vector machines, and convolutional neural networks (CNNs). The MothNet architecture illustrates how our proposed algorithmic structures, derived from biological brains, can be used to build alternative deep neural nets (DNNs) that may potentially avoid some of DNNs current learning rate limitations. This novel, bio-inspired neural network architecture offers a valuable complementary approach to DNN design.

Biological Mechanisms for Learning: A Computational Model of Olfactory Learning in the Manduca sexta Moth, with Applications to Neural Nets

The insect olfactory system, which includes the antennal lobe (AL), mushroom body (MB), and ancillary structures, is a relatively simple neural system capable of learning. Its structural features, which are widespread in biological neural systems, process olfactory stimuli through a cascade of networks where large dimension shifts occur from stage to stage and where sparsity and randomness play a critical role in coding. Learning is partly enabled by a neuromodulatory reward mechanism of octopamine stimulation of the AL, whose increased activity induces rewiring of the MB through Hebbian plasticity. Enforced sparsity in the MB focuses Hebbian growth on neurons that are the most important for the representation of the learned odor. Based upon current biophysical knowledge, we have constructed an end-to-end computational model of the Manduca sexta moth olfactory system which includes the interaction of the AL and MB under octopamine stimulation. Our model is able to robustly learn new odors, and our simulations of integrate-and-fire neurons match the statistical features of in-vivo firing rate data. From a biological perspective, the model provides a valuable tool for examining the role of neuromodulators, like octopamine, in learning, and gives insight into critical interactions between sparsity, Hebbian growth, and stimulation during learning. Our simulations also inform predictions about structural details of the olfactory system that are not currently well-characterized. From a machine learning perspective, the model yields bio-inspired mechanisms that are potentially useful in constructing neural nets for rapid learning from very few samples. These mechanisms include high-noise layers, sparse layers as noise filters, and a biologically-plausible optimization method to train the network based on octopamine stimulation, sparse layers, and Hebbian growth.