A proof-of-concept for automated AI-driven stellarator coil optimization with in-the-loop finite-element calculations

Finding feasible coils for stellarator fusion devices is a critical challenge of realizing this concept for future power plants. Years of research work can be put into the design of even a single reactor-scale stellarator design. To rapidly speed up and automate the workflow of designing stellarator coils, we have designed an end-to-end ``runner'' for performing stellarator coil optimization. The entirety of pre and post-processing steps have been automated; the user specifies only a few basic input parameters, and final coil solutions are updated on an open-source leaderboard. Two policies are available for performing non-stop automated coil optimizations through a genetic algorithm or a context-aware LLM. Lastly, we construct a novel in-the-loop optimization of Von Mises stresses in the coils, opening up important future capabilities for in-the-loop finite-element calculations.

Grad-Shafranov equilibria via data-free physics informed neural networks

A large number of magnetohydrodynamic (MHD) equilibrium calculations are often required for uncertainty quantification, optimization, and real-time diagnostic information, making MHD equilibrium codes vital to the field of plasma physics. In this paper, we explore a method for solving the Grad-Shafranov equation by using Physics-Informed Neural Networks (PINNs). For PINNs, we optimize neural networks by directly minimizing the residual of the PDE as a loss function. We show that PINNs can accurately and effectively solve the Grad-Shafranov equation with several different boundary conditions. We also explore the parameter space by varying the size of the model, the learning rate, and boundary conditions to map various trade-offs such as between reconstruction error and computational speed. Additionally, we introduce a parameterized PINN framework, expanding the input space to include variables such as pressure, aspect ratio, elongation, and triangularity in order to handle a broader range of plasma scenarios within a single network. Parametrized PINNs could be used in future work to solve inverse problems such as shape optimization.

Benchmarking sparse system identification with low-dimensional chaos

Sparse system identification is the data-driven process of obtaining parsimonious differential equations that describe the evolution of a dynamical system, balancing model complexity and accuracy. There has been rapid innovation in system identification across scientific domains, but there remains a gap in the literature for large-scale methodological comparisons that are evaluated on a variety of dynamical systems. In this work, we systematically benchmark sparse regression variants by utilizing the dysts standardized database of chaotic systems. In particular, we demonstrate how this open-source tool can be used to quantitatively compare different methods of system identification. To illustrate how this benchmark can be utilized, we perform a large comparison of four algorithms for solving the sparse identification of nonlinear dynamics (SINDy) optimization problem, finding strong performance of the original algorithm and a recent mixed-integer discrete algorithm. In all cases, we used ensembling to improve the noise robustness of SINDy and provide statistical comparisons. In addition, we show very compelling evidence that the weak SINDy formulation provides significant improvements over the traditional method, even on clean data. Lastly, we investigate how Pareto-optimal models generated from SINDy algorithms depend on the properties of the equations, finding that the performance shows no significant dependence on a set of dynamical properties that quantify the amount of chaos, scale separation, degree of nonlinearity, and the syntactic complexity.

PySINDy: A comprehensive Python package for robust sparse system identification

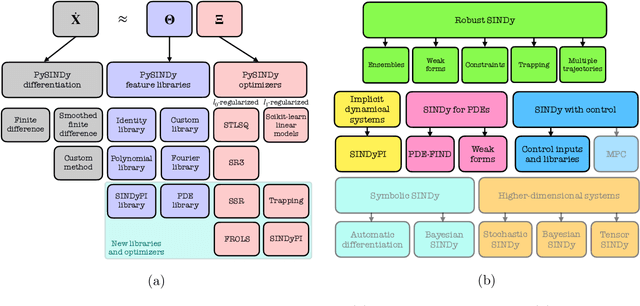
Automated data-driven modeling, the process of directly discovering the governing equations of a system from data, is increasingly being used across the scientific community. PySINDy is a Python package that provides tools for applying the sparse identification of nonlinear dynamics (SINDy) approach to data-driven model discovery. In this major update to PySINDy, we implement several advanced features that enable the discovery of more general differential equations from noisy and limited data. The library of candidate terms is extended for the identification of actuated systems, partial differential equations (PDEs), and implicit differential equations. Robust formulations, including the integral form of SINDy and ensembling techniques, are also implemented to improve performance for real-world data. Finally, we provide a range of new optimization algorithms, including several sparse regression techniques and algorithms to enforce and promote inequality constraints and stability. Together, these updates enable entirely new SINDy model discovery capabilities that have not been reported in the literature, such as constrained PDE identification and ensembling with different sparse regression optimizers.