The Experimental Multi-Arm Pendulum on a Cart: A Benchmark System for Chaos, Learning, and Control

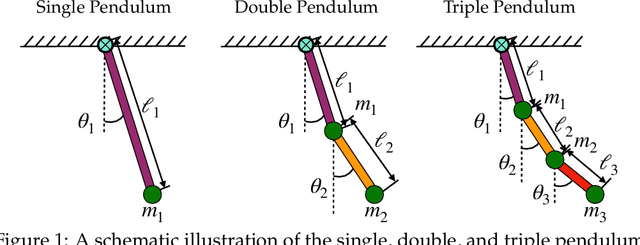
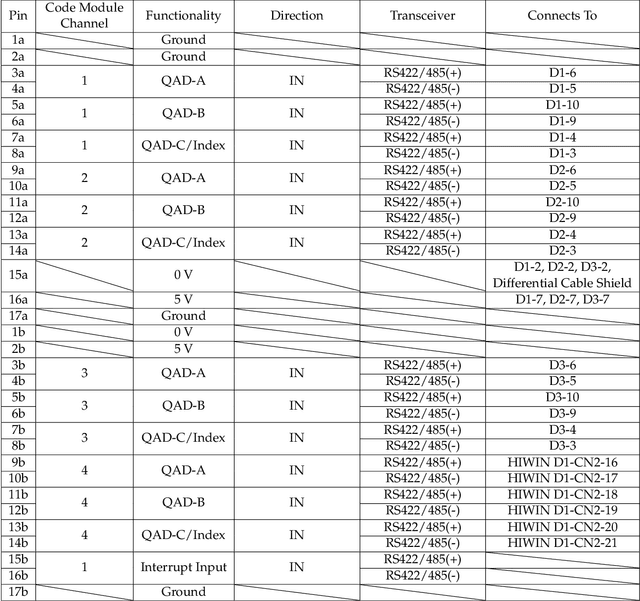
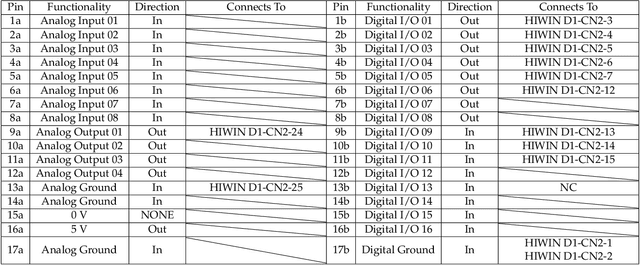
The single, double, and triple pendulum has served as an illustrative experimental benchmark system for scientists to study dynamical behavior for more than four centuries. The pendulum system exhibits a wide range of interesting behaviors, from simple harmonic motion in the single pendulum to chaotic dynamics in multi-arm pendulums. Under forcing, even the single pendulum may exhibit chaos, providing a simple example of a damped-driven system. All multi-armed pendulums are characterized by the existence of index-one saddle points, which mediate the transport of trajectories in the system, providing a simple mechanical analog of various complex transport phenomena, from biolocomotion to transport within the solar system. Further, pendulum systems have long been used to design and test both linear and nonlinear control strategies, with the addition of more arms making the problem more challenging. In this work, we provide extensive designs for the construction and operation of a high-performance, multi-link pendulum on a cart system. Although many experimental setups have been built to study the behavior of pendulum systems, such an extensive documentation on the design, construction, and operation is missing from the literature. The resulting experimental system is highly flexible, enabling a wide range of benchmark problems in dynamical systems modeling, system identification and learning, and control. To promote reproducible research, we have made our entire system open-source, including 3D CAD drawings, basic tutorial code, and data. Moreover, we discuss the possibility of extending our system capability to be operated remotely to enable researchers all around the world to use it, thus increasing access.

Learning Discrepancy Models From Experimental Data

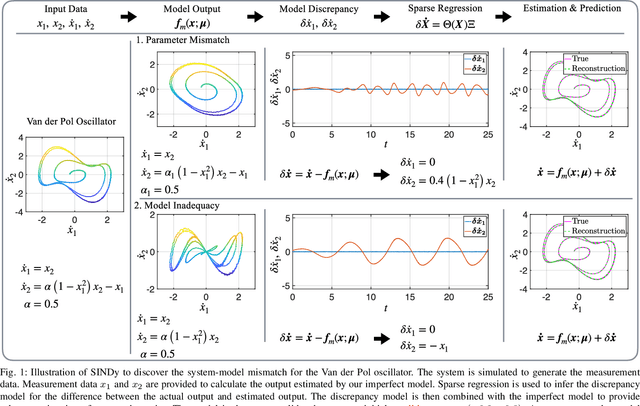
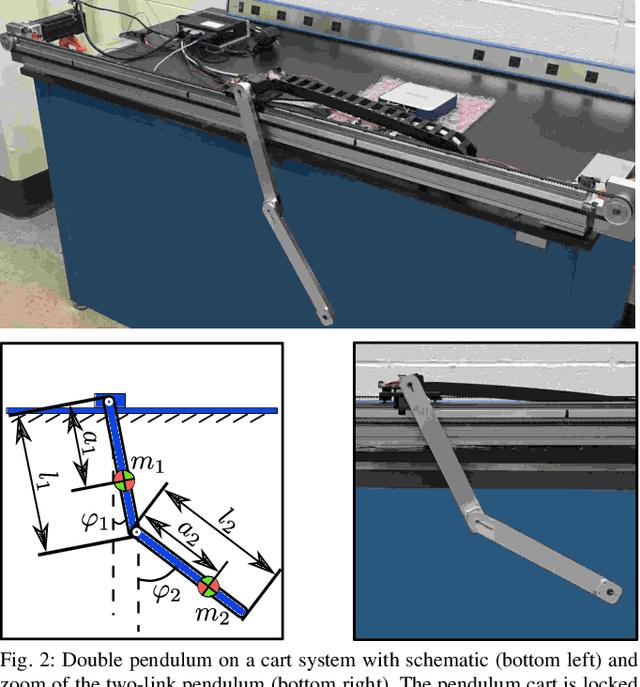
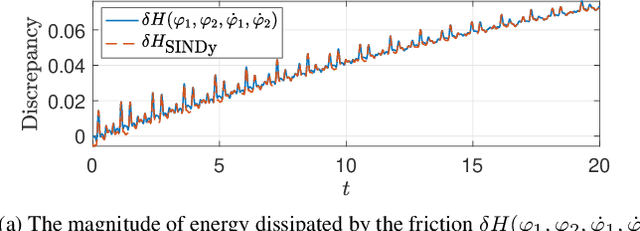
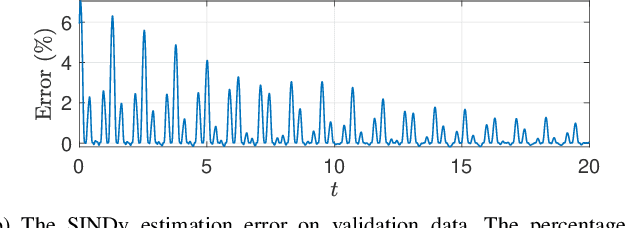
First principles modeling of physical systems has led to significant technological advances across all branches of science. For nonlinear systems, however, small modeling errors can lead to significant deviations from the true, measured behavior. Even in mechanical systems, where the equations are assumed to be well-known, there are often model discrepancies corresponding to nonlinear friction, wind resistance, etc. Discovering models for these discrepancies remains an open challenge for many complex systems. In this work, we use the sparse identification of nonlinear dynamics (SINDy) algorithm to discover a model for the discrepancy between a simplified model and measurement data. In particular, we assume that the model mismatch can be sparsely represented in a library of candidate model terms. We demonstrate the efficacy of our approach on several examples including experimental data from a double pendulum on a cart. We further design and implement a feed-forward controller in simulations, showing improvement with a discrepancy model.