Real-Time Motion Detection Using Dynamic Mode Decomposition

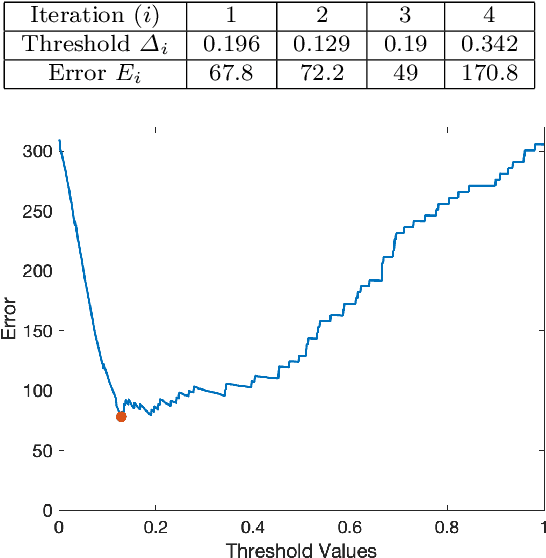
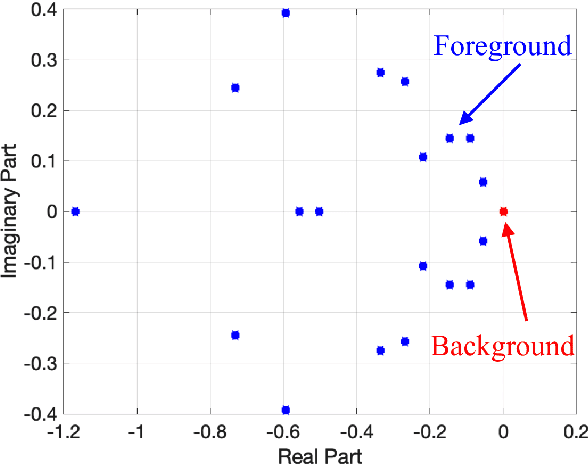
Dynamic Mode Decomposition (DMD) is a numerical method that seeks to fit timeseries data to a linear dynamical system. In doing so, DMD decomposes dynamic data into spatially coherent modes that evolve in time according to exponential growth/decay or with a fixed frequency of oscillation. A prolific application of DMD has been to video, where one interprets the high-dimensional pixel space evolving through time as the video plays. In this work, we propose a simple and interpretable motion detection algorithm for streaming video data rooted in DMD. Our method leverages the fact that there exists a correspondence between the evolution of important video features, such as foreground motion, and the eigenvalues of the matrix which results from applying DMD to segments of video. We apply the method to a database of test videos which emulate security footage under varying realistic conditions. Effectiveness is analyzed using receiver operating characteristic curves, while we use cross-validation to optimize the threshold parameter that identifies movement.

Transferability of Graph Neural Networks using Graphon and Sampling Theories

Graph neural networks (GNNs) have become powerful tools for processing graph-based information in various domains. A desirable property of GNNs is transferability, where a trained network can swap in information from a different graph without retraining and retain its accuracy. A recent method of capturing transferability of GNNs is through the use of graphons, which are symmetric, measurable functions representing the limit of large dense graphs. In this work, we contribute to the application of graphons to GNNs by presenting an explicit two-layer graphon neural network (WNN) architecture. We prove its ability to approximate bandlimited signals within a specified error tolerance using a minimal number of network weights. We then leverage this result, to establish the transferability of an explicit two-layer GNN over all sufficiently large graphs in a sequence converging to a graphon. Our work addresses transferability between both deterministic weighted graphs and simple random graphs and overcomes issues related to the curse of dimensionality that arise in other GNN results. The proposed WNN and GNN architectures offer practical solutions for handling graph data of varying sizes while maintaining performance guarantees without extensive retraining.

Auxiliary Functions as Koopman Observables: Data-Driven Polynomial Optimization for Dynamical Systems

We present a flexible data-driven method for dynamical system analysis that does not require explicit model discovery. The method is rooted in well-established techniques for approximating the Koopman operator from data and is implemented as a semidefinite program that can be solved numerically. The method is agnostic of whether data is generated through a deterministic or stochastic process, so its implementation requires no prior adjustments by the user to accommodate these different scenarios. Rigorous convergence results justify the applicability of the method, while also extending and uniting similar results from across the literature. Examples on discovering Lyapunov functions and on performing ergodic optimization for both deterministic and stochastic dynamics exemplify these convergence results and demonstrate the performance of the method.

The Experimental Multi-Arm Pendulum on a Cart: A Benchmark System for Chaos, Learning, and Control

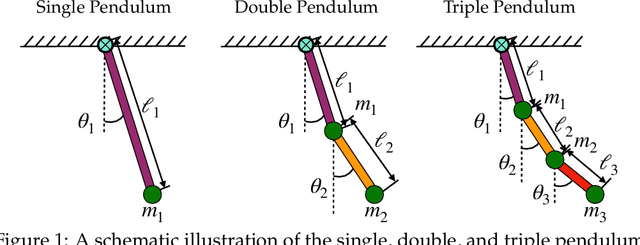
The single, double, and triple pendulum has served as an illustrative experimental benchmark system for scientists to study dynamical behavior for more than four centuries. The pendulum system exhibits a wide range of interesting behaviors, from simple harmonic motion in the single pendulum to chaotic dynamics in multi-arm pendulums. Under forcing, even the single pendulum may exhibit chaos, providing a simple example of a damped-driven system. All multi-armed pendulums are characterized by the existence of index-one saddle points, which mediate the transport of trajectories in the system, providing a simple mechanical analog of various complex transport phenomena, from biolocomotion to transport within the solar system. Further, pendulum systems have long been used to design and test both linear and nonlinear control strategies, with the addition of more arms making the problem more challenging. In this work, we provide extensive designs for the construction and operation of a high-performance, multi-link pendulum on a cart system. Although many experimental setups have been built to study the behavior of pendulum systems, such an extensive documentation on the design, construction, and operation is missing from the literature. The resulting experimental system is highly flexible, enabling a wide range of benchmark problems in dynamical systems modeling, system identification and learning, and control. To promote reproducible research, we have made our entire system open-source, including 3D CAD drawings, basic tutorial code, and data. Moreover, we discuss the possibility of extending our system capability to be operated remotely to enable researchers all around the world to use it, thus increasing access.

Deep Learning of Conjugate Mappings

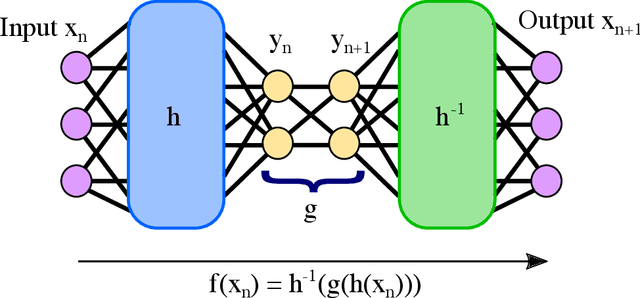
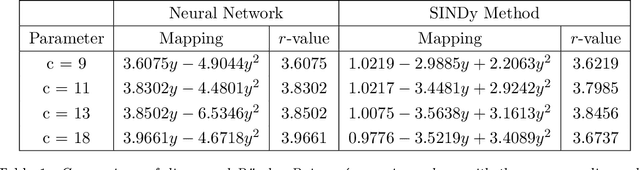
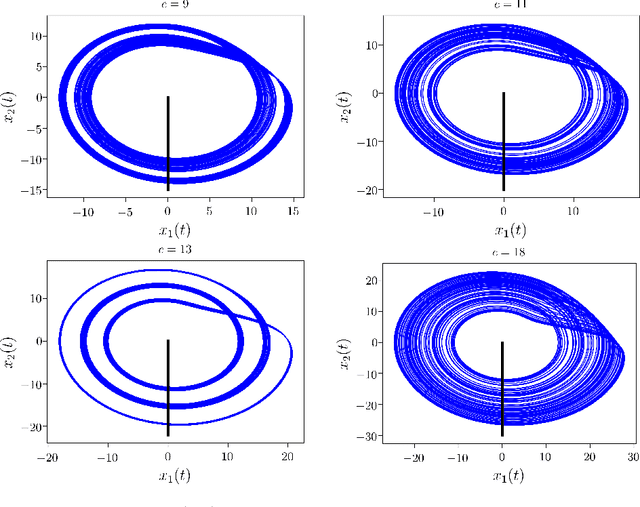
Despite many of the most common chaotic dynamical systems being continuous in time, it is through discrete time mappings that much of the understanding of chaos is formed. Henri Poincar\'e first made this connection by tracking consecutive iterations of the continuous flow with a lower-dimensional, transverse subspace. The mapping that iterates the dynamics through consecutive intersections of the flow with the subspace is now referred to as a Poincar\'e map, and it is the primary method available for interpreting and classifying chaotic dynamics. Unfortunately, in all but the simplest systems, an explicit form for such a mapping remains outstanding. This work proposes a method for obtaining explicit Poincar\'e mappings by using deep learning to construct an invertible coordinate transformation into a conjugate representation where the dynamics are governed by a relatively simple chaotic mapping. The invertible change of variable is based on an autoencoder, which allows for dimensionality reduction, and has the advantage of classifying chaotic systems using the equivalence relation of topological conjugacies. Indeed, the enforcement of topological conjugacies is the critical neural network regularization for learning the coordinate and dynamics pairing. We provide expository applications of the method to low-dimensional systems such as the R\"ossler and Lorenz systems, while also demonstrating the utility of the method on infinite-dimensional systems, such as the Kuramoto--Sivashinsky equation.

Sparse Identification of Slow Timescale Dynamics

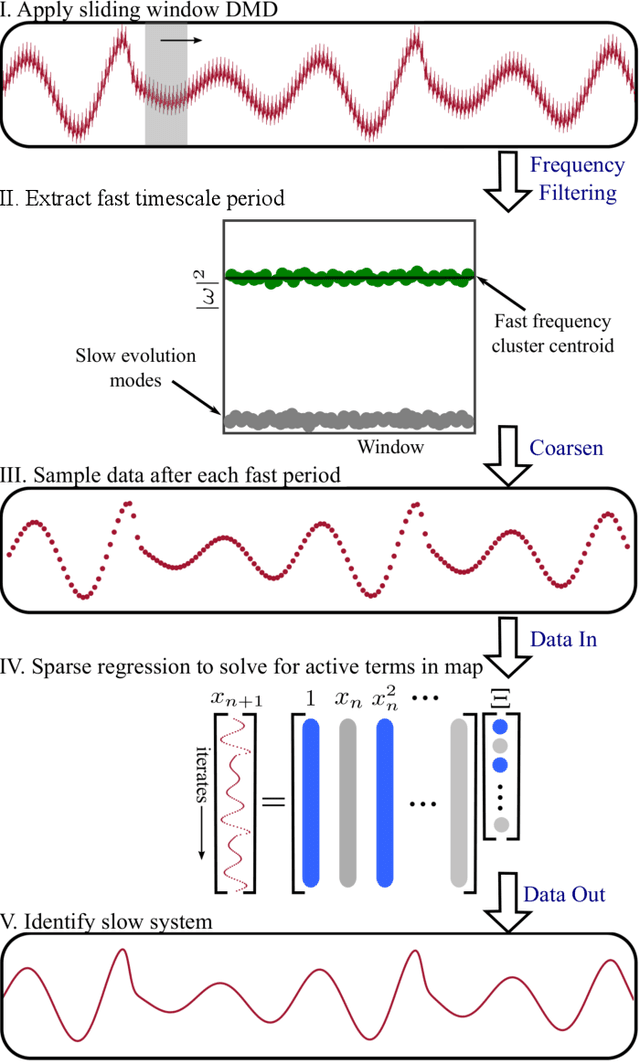
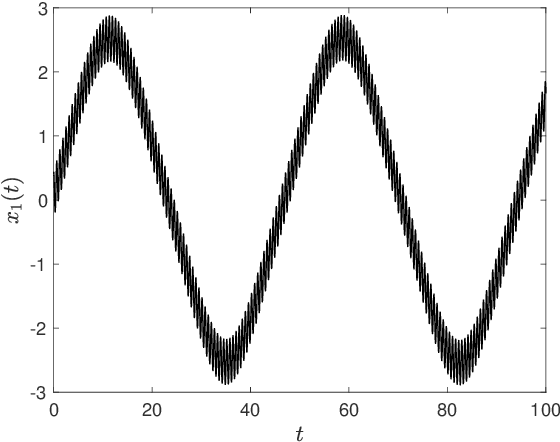
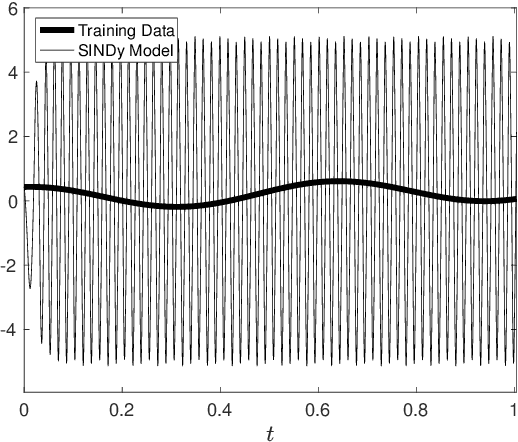
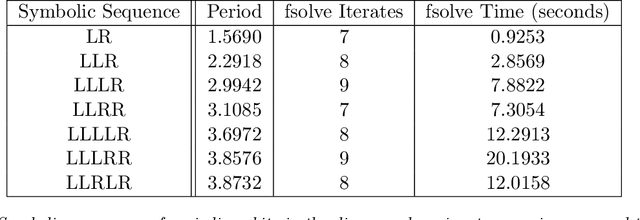
Multiscale phenomena that evolve on multiple distinct timescales are prevalent throughout the sciences. It is often the case that the governing equations of the persistent and approximately periodic fast scales are prescribed, while the emergent slow scale evolution is unknown. Yet the course-grained, slow scale dynamics is often of greatest interest in practice. In this work we present an accurate and efficient method for extracting the slow timescale dynamics from a signal exhibiting multiple timescales. The method relies on tracking the signal at evenly-spaced intervals with length given by the period of the fast timescale, which is discovered using clustering techniques in conjunction with the dynamic mode decomposition. Sparse regression techniques are then used to discover a mapping which describes iterations from one data point to the next. We show that for sufficiently disparate timescales this discovered mapping can be used to discover the continuous-time slow dynamics, thus providing a novel tool for extracting dynamics on multiple timescales.