Sparse Identification of Slow Timescale Dynamics

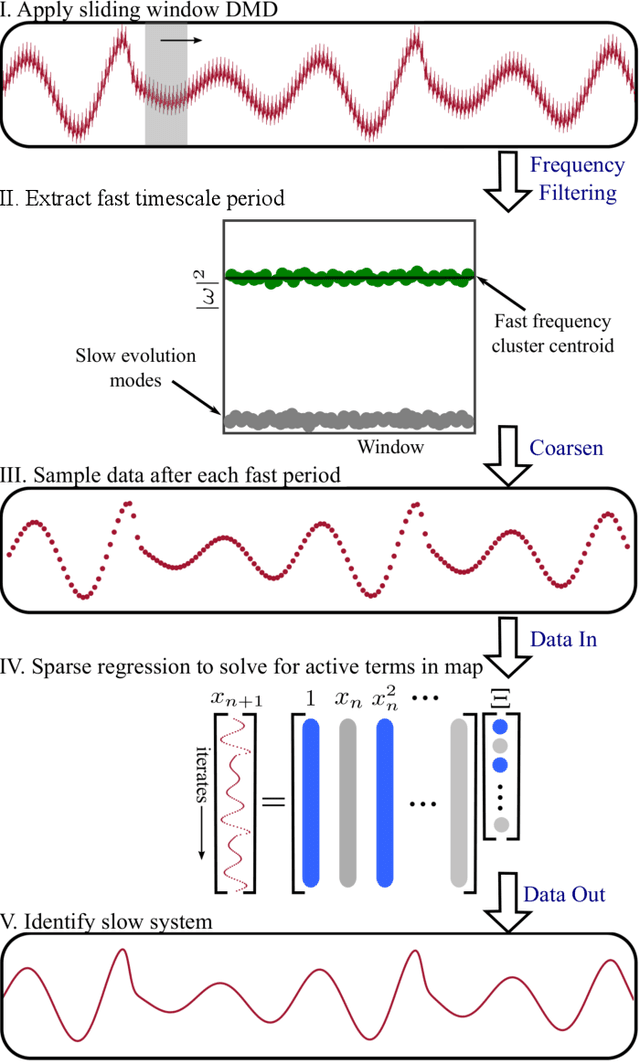
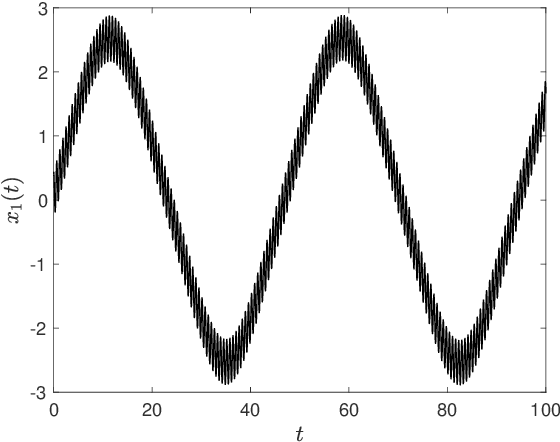
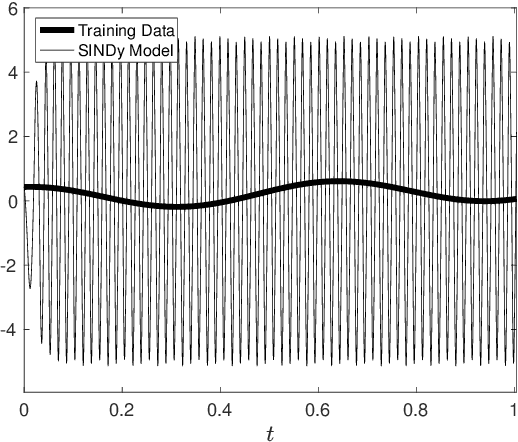
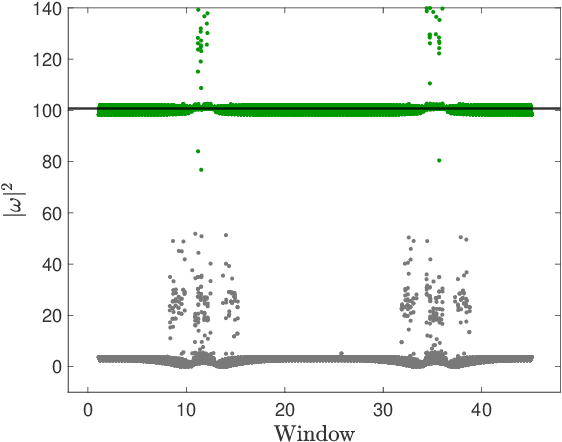
Multiscale phenomena that evolve on multiple distinct timescales are prevalent throughout the sciences. It is often the case that the governing equations of the persistent and approximately periodic fast scales are prescribed, while the emergent slow scale evolution is unknown. Yet the course-grained, slow scale dynamics is often of greatest interest in practice. In this work we present an accurate and efficient method for extracting the slow timescale dynamics from a signal exhibiting multiple timescales. The method relies on tracking the signal at evenly-spaced intervals with length given by the period of the fast timescale, which is discovered using clustering techniques in conjunction with the dynamic mode decomposition. Sparse regression techniques are then used to discover a mapping which describes iterations from one data point to the next. We show that for sufficiently disparate timescales this discovered mapping can be used to discover the continuous-time slow dynamics, thus providing a novel tool for extracting dynamics on multiple timescales.