Efficient Learning Using Spiking Neural Networks Equipped With Affine Encoders and Decoders

We study the learning problem associated with spiking neural networks. Specifically, we consider hypothesis sets of spiking neural networks with affine temporal encoders and decoders and simple spiking neurons having only positive synaptic weights. We demonstrate that the positivity of the weights continues to enable a wide range of expressivity results, including rate-optimal approximation of smooth functions or approximation without the curse of dimensionality. Moreover, positive-weight spiking neural networks are shown to depend continuously on their parameters which facilitates classical covering number-based generalization statements. Finally, we observe that from a generalization perspective, contrary to feedforward neural networks or previous results for general spiking neural networks, the depth has little to no adverse effect on the generalization capabilities.

Digital Computers Break the Curse of Dimensionality: Adaptive Bounds via Finite Geometry

Many of the foundations of machine learning rely on the idealized premise that all input and output spaces are infinite, e.g.~$\mathbb{R}^d$. This core assumption is systematically violated in practice due to digital computing limitations from finite machine precision, rounding, and limited RAM. In short, digital computers operate on finite grids in $\mathbb{R}^d$. By exploiting these discrete structures, we show the curse of dimensionality in statistical learning is systematically broken when models are implemented on real computers. Consequentially, we obtain new generalization bounds with dimension-free rates for kernel and deep ReLU MLP regressors, which are implemented on real-world machines. Our results are derived using a new non-asymptotic concentration of measure result between a probability measure over any finite metric space and its empirical version associated with $N$ i.i.d. samples when measured in the $1$-Wasserstein distance. Unlike standard concentration of measure results, the concentration rates in our bounds do not hold uniformly for all sample sizes $N$; instead, our rates can adapt to any given $N$. This yields significantly tighter bounds for realistic sample sizes while achieving the optimal worst-case rate of $\mathcal{O}(1/N^{1/2})$ for massive. Our results are built on new techniques combining metric embedding theory with optimal transport

Transferability of Graph Neural Networks using Graphon and Sampling Theories

Graph neural networks (GNNs) have become powerful tools for processing graph-based information in various domains. A desirable property of GNNs is transferability, where a trained network can swap in information from a different graph without retraining and retain its accuracy. A recent method of capturing transferability of GNNs is through the use of graphons, which are symmetric, measurable functions representing the limit of large dense graphs. In this work, we contribute to the application of graphons to GNNs by presenting an explicit two-layer graphon neural network (WNN) architecture. We prove its ability to approximate bandlimited signals within a specified error tolerance using a minimal number of network weights. We then leverage this result, to establish the transferability of an explicit two-layer GNN over all sufficiently large graphs in a sequence converging to a graphon. Our work addresses transferability between both deterministic weighted graphs and simple random graphs and overcomes issues related to the curse of dimensionality that arise in other GNN results. The proposed WNN and GNN architectures offer practical solutions for handling graph data of varying sizes while maintaining performance guarantees without extensive retraining.

Graph Laplacians on Shared Nearest Neighbor graphs and graph Laplacians on $k$-Nearest Neighbor graphs having the same limit

A Shared Nearest Neighbor (SNN) graph is a type of graph construction using shared nearest neighbor information, which is a secondary similarity measure based on the rankings induced by a primary $k$-nearest neighbor ($k$-NN) measure. SNN measures have been touted as being less prone to the curse of dimensionality than conventional distance measures, and thus methods using SNN graphs have been widely used in applications, particularly in clustering high-dimensional data sets and in finding outliers in subspaces of high dimensional data. Despite this, the theoretical study of SNN graphs and graph Laplacians remains unexplored. In this pioneering work, we make the first contribution in this direction. We show that large scale asymptotics of an SNN graph Laplacian reach a consistent continuum limit; this limit is the same as that of a $k$-NN graph Laplacian. Moreover, we show that the pointwise convergence rate of the graph Laplacian is linear with respect to $(k/n)^{1/m}$ with high probability.

Superiority of GNN over NN in generalizing bandlimited functions

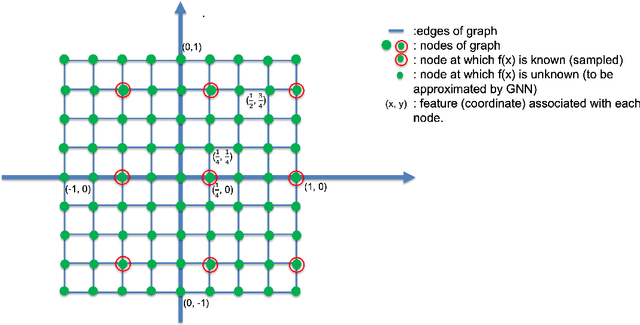
We constructively show, via rigorous mathematical arguments, that GNN architectures outperform those of NN in approximating bandlimited functions on compact $d$-dimensional Euclidean grids. We show that the former only need $\mathcal{M}$ sampled functional values in order to achieve a uniform approximation error of $O_{d}(2^{-\mathcal{M}^{1/d}})$ and that this error rate is optimal, in the sense that, NNs might achieve worse.