Superiority of GNN over NN in generalizing bandlimited functions
Paper and Code
Jun 13, 2022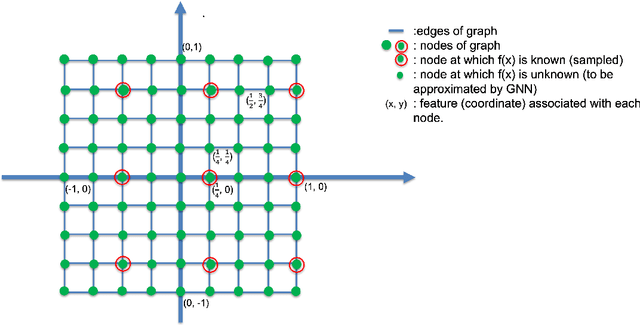
We constructively show, via rigorous mathematical arguments, that GNN architectures outperform those of NN in approximating bandlimited functions on compact $d$-dimensional Euclidean grids. We show that the former only need $\mathcal{M}$ sampled functional values in order to achieve a uniform approximation error of $O_{d}(2^{-\mathcal{M}^{1/d}})$ and that this error rate is optimal, in the sense that, NNs might achieve worse.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge