Consistency of augmentation graph and network approximability in contrastive learning

Contrastive learning leverages data augmentation to develop feature representation without relying on large labeled datasets. However, despite its empirical success, the theoretical foundations of contrastive learning remain incomplete, with many essential guarantees left unaddressed, particularly the realizability assumption concerning neural approximability of an optimal spectral contrastive loss solution. In this work, we overcome these limitations by analyzing the pointwise and spectral consistency of the augmentation graph Laplacian. We establish that, under specific conditions for data generation and graph connectivity, as the augmented dataset size increases, the augmentation graph Laplacian converges to a weighted Laplace-Beltrami operator on the natural data manifold. These consistency results ensure that the graph Laplacian spectrum effectively captures the manifold geometry. Consequently, they give way to a robust framework for establishing neural approximability, directly resolving the realizability assumption in a current paradigm.

Universal Facial Encoding of Codec Avatars from VR Headsets

Faithful real-time facial animation is essential for avatar-mediated telepresence in Virtual Reality (VR). To emulate authentic communication, avatar animation needs to be efficient and accurate: able to capture both extreme and subtle expressions within a few milliseconds to sustain the rhythm of natural conversations. The oblique and incomplete views of the face, variability in the donning of headsets, and illumination variation due to the environment are some of the unique challenges in generalization to unseen faces. In this paper, we present a method that can animate a photorealistic avatar in realtime from head-mounted cameras (HMCs) on a consumer VR headset. We present a self-supervised learning approach, based on a cross-view reconstruction objective, that enables generalization to unseen users. We present a lightweight expression calibration mechanism that increases accuracy with minimal additional cost to run-time efficiency. We present an improved parameterization for precise ground-truth generation that provides robustness to environmental variation. The resulting system produces accurate facial animation for unseen users wearing VR headsets in realtime. We compare our approach to prior face-encoding methods demonstrating significant improvements in both quantitative metrics and qualitative results.

Spectral Neural Networks: Approximation Theory and Optimization Landscape

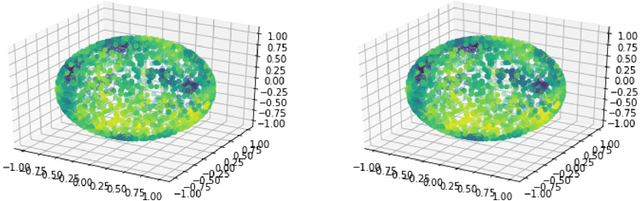
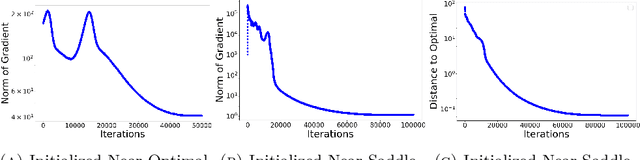
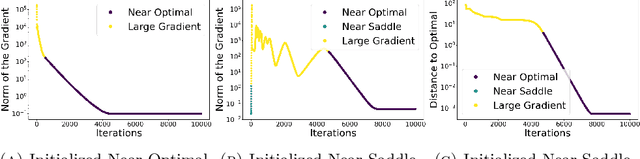
There is a large variety of machine learning methodologies that are based on the extraction of spectral geometric information from data. However, the implementations of many of these methods often depend on traditional eigensolvers, which present limitations when applied in practical online big data scenarios. To address some of these challenges, researchers have proposed different strategies for training neural networks as alternatives to traditional eigensolvers, with one such approach known as Spectral Neural Network (SNN). In this paper, we investigate key theoretical aspects of SNN. First, we present quantitative insights into the tradeoff between the number of neurons and the amount of spectral geometric information a neural network learns. Second, we initiate a theoretical exploration of the optimization landscape of SNN's objective to shed light on the training dynamics of SNN. Unlike typical studies of convergence to global solutions of NN training dynamics, SNN presents an additional complexity due to its non-convex ambient loss function.

Auto-CARD: Efficient and Robust Codec Avatar Driving for Real-time Mobile Telepresence

Real-time and robust photorealistic avatars for telepresence in AR/VR have been highly desired for enabling immersive photorealistic telepresence. However, there still exists one key bottleneck: the considerable computational expense needed to accurately infer facial expressions captured from headset-mounted cameras with a quality level that can match the realism of the avatar's human appearance. To this end, we propose a framework called Auto-CARD, which for the first time enables real-time and robust driving of Codec Avatars when exclusively using merely on-device computing resources. This is achieved by minimizing two sources of redundancy. First, we develop a dedicated neural architecture search technique called AVE-NAS for avatar encoding in AR/VR, which explicitly boosts both the searched architectures' robustness in the presence of extreme facial expressions and hardware friendliness on fast evolving AR/VR headsets. Second, we leverage the temporal redundancy in consecutively captured images during continuous rendering and develop a mechanism dubbed LATEX to skip the computation of redundant frames. Specifically, we first identify an opportunity from the linearity of the latent space derived by the avatar decoder and then propose to perform adaptive latent extrapolation for redundant frames. For evaluation, we demonstrate the efficacy of our Auto-CARD framework in real-time Codec Avatar driving settings, where we achieve a 5.05x speed-up on Meta Quest 2 while maintaining a comparable or even better animation quality than state-of-the-art avatar encoder designs.

A Fast Scale-Invariant Algorithm for Non-negative Least Squares with Non-negative Data

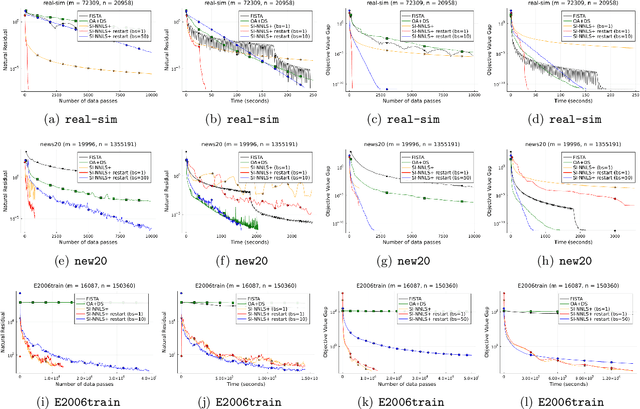
Nonnegative (linear) least square problems are a fundamental class of problems that is well-studied in statistical learning and for which solvers have been implemented in many of the standard programming languages used within the machine learning community. The existing off-the-shelf solvers view the non-negativity constraint in these problems as an obstacle and, compared to unconstrained least squares, perform additional effort to address it. However, in many of the typical applications, the data itself is nonnegative as well, and we show that the nonnegativity in this case makes the problem easier. In particular, while the oracle complexity of unconstrained least squares problems necessarily scales with one of the data matrix constants (typically the spectral norm) and these problems are solved to additive error, we show that nonnegative least squares problems with nonnegative data are solvable to multiplicative error and with complexity that is independent of any matrix constants. The algorithm we introduce is accelerated and based on a primal-dual perspective. We further show how to provably obtain linear convergence using adaptive restart coupled with our method and demonstrate its effectiveness on large-scale data via numerical experiments.

Large sample spectral analysis of graph-based multi-manifold clustering

In this work we study statistical properties of graph-based algorithms for multi-manifold clustering (MMC). In MMC the goal is to retrieve the multi-manifold structure underlying a given Euclidean data set when this one is assumed to be obtained by sampling a distribution on a union of manifolds $\mathcal{M} = \mathcal{M}_1 \cup\dots \cup \mathcal{M}_N$ that may intersect with each other and that may have different dimensions. We investigate sufficient conditions that similarity graphs on data sets must satisfy in order for their corresponding graph Laplacians to capture the right geometric information to solve the MMC problem. Precisely, we provide high probability error bounds for the spectral approximation of a tensorized Laplacian on $\mathcal{M}$ with a suitable graph Laplacian built from the observations; the recovered tensorized Laplacian contains all geometric information of all the individual underlying manifolds. We provide an example of a family of similarity graphs, which we call annular proximity graphs with angle constraints, satisfying these sufficient conditions. We contrast our family of graphs with other constructions in the literature based on the alignment of tangent planes. Extensive numerical experiments expand the insights that our theory provides on the MMC problem.