A Fast Scale-Invariant Algorithm for Non-negative Least Squares with Non-negative Data
Paper and Code
Mar 08, 2022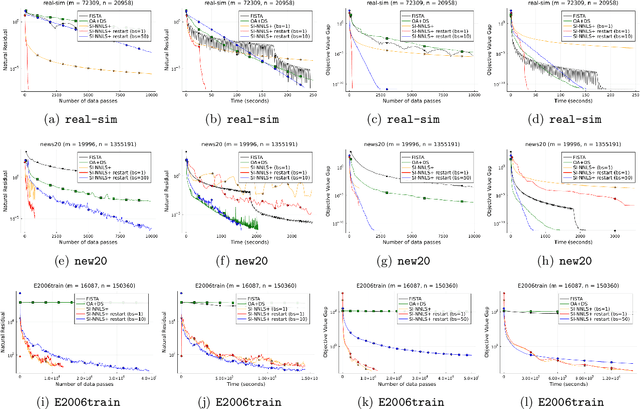
Nonnegative (linear) least square problems are a fundamental class of problems that is well-studied in statistical learning and for which solvers have been implemented in many of the standard programming languages used within the machine learning community. The existing off-the-shelf solvers view the non-negativity constraint in these problems as an obstacle and, compared to unconstrained least squares, perform additional effort to address it. However, in many of the typical applications, the data itself is nonnegative as well, and we show that the nonnegativity in this case makes the problem easier. In particular, while the oracle complexity of unconstrained least squares problems necessarily scales with one of the data matrix constants (typically the spectral norm) and these problems are solved to additive error, we show that nonnegative least squares problems with nonnegative data are solvable to multiplicative error and with complexity that is independent of any matrix constants. The algorithm we introduce is accelerated and based on a primal-dual perspective. We further show how to provably obtain linear convergence using adaptive restart coupled with our method and demonstrate its effectiveness on large-scale data via numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge