Accelerated Cyclic Coordinate Dual Averaging with Extrapolation for Composite Convex Optimization

Exploiting partial first-order information in a cyclic way is arguably the most natural strategy to obtain scalable first-order methods. However, despite their wide use in practice, cyclic schemes are far less understood from a theoretical perspective than their randomized counterparts. Motivated by a recent success in analyzing an extrapolated cyclic scheme for generalized variational inequalities, we propose an Accelerated Cyclic Coordinate Dual Averaging with Extrapolation (A-CODER) method for composite convex optimization, where the objective function can be expressed as the sum of a smooth convex function accessible via a gradient oracle and a convex, possibly nonsmooth, function accessible via a proximal oracle. We show that A-CODER attains the optimal convergence rate with improved dependence on the number of blocks compared to prior work. Furthermore, for the setting where the smooth component of the objective function is expressible in a finite sum form, we introduce a variance-reduced variant of A-CODER, VR-A-CODER, with state-of-the-art complexity guarantees. Finally, we demonstrate the effectiveness of our algorithms through numerical experiments.

Cyclic Block Coordinate Descent With Variance Reduction for Composite Nonconvex Optimization

Nonconvex optimization is central in solving many machine learning problems, in which block-wise structure is commonly encountered. In this work, we propose cyclic block coordinate methods for nonconvex optimization problems with non-asymptotic gradient norm guarantees. Our convergence analysis is based on a gradient Lipschitz condition with respect to a Mahalanobis norm, inspired by a recent progress on cyclic block coordinate methods. In deterministic settings, our convergence guarantee matches the guarantee of (full-gradient) gradient descent, but with the gradient Lipschitz constant being defined w.r.t.~the Mahalanobis norm. In stochastic settings, we use recursive variance reduction to decrease the per-iteration cost and match the arithmetic operation complexity of current optimal stochastic full-gradient methods, with a unified analysis for both finite-sum and infinite-sum cases. We further prove the faster, linear convergence of our methods when a Polyak-{\L}ojasiewicz (P{\L}) condition holds for the objective function. To the best of our knowledge, our work is the first to provide variance-reduced convergence guarantees for a cyclic block coordinate method. Our experimental results demonstrate the efficacy of the proposed variance-reduced cyclic scheme in training deep neural nets.

A Stochastic Halpern Iteration with Variance Reduction for Stochastic Monotone Inclusion Problems

We study stochastic monotone inclusion problems, which widely appear in machine learning applications, including robust regression and adversarial learning. We propose novel variants of stochastic Halpern iteration with recursive variance reduction. In the cocoercive -- and more generally Lipschitz-monotone -- setup, our algorithm attains $\epsilon$ norm of the operator with $\mathcal{O}(\frac{1}{\epsilon^3})$ stochastic operator evaluations, which significantly improves over state of the art $\mathcal{O}(\frac{1}{\epsilon^4})$ stochastic operator evaluations required for existing monotone inclusion solvers applied to the same problem classes. We further show how to couple one of the proposed variants of stochastic Halpern iteration with a scheduled restart scheme to solve stochastic monotone inclusion problems with ${\mathcal{O}}(\frac{\log(1/\epsilon)}{\epsilon^2})$ stochastic operator evaluations under additional sharpness or strong monotonicity assumptions. Finally, we argue via reductions between different problem classes that our stochastic oracle complexity bounds are tight up to logarithmic factors in terms of their $\epsilon$-dependence.

A Fast Scale-Invariant Algorithm for Non-negative Least Squares with Non-negative Data

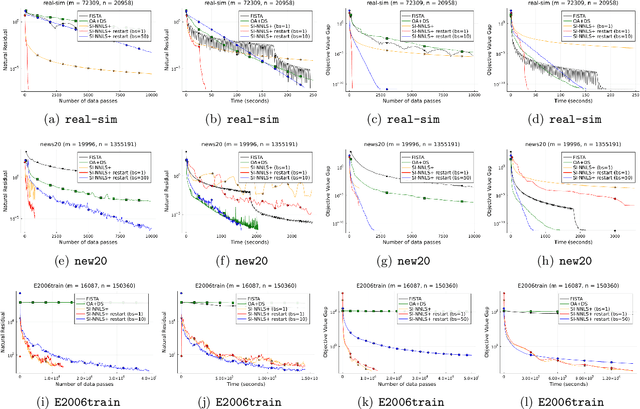
Nonnegative (linear) least square problems are a fundamental class of problems that is well-studied in statistical learning and for which solvers have been implemented in many of the standard programming languages used within the machine learning community. The existing off-the-shelf solvers view the non-negativity constraint in these problems as an obstacle and, compared to unconstrained least squares, perform additional effort to address it. However, in many of the typical applications, the data itself is nonnegative as well, and we show that the nonnegativity in this case makes the problem easier. In particular, while the oracle complexity of unconstrained least squares problems necessarily scales with one of the data matrix constants (typically the spectral norm) and these problems are solved to additive error, we show that nonnegative least squares problems with nonnegative data are solvable to multiplicative error and with complexity that is independent of any matrix constants. The algorithm we introduce is accelerated and based on a primal-dual perspective. We further show how to provably obtain linear convergence using adaptive restart coupled with our method and demonstrate its effectiveness on large-scale data via numerical experiments.

Coordinate Linear Variance Reduction for Generalized Linear Programming

We study a class of generalized linear programs (GLP) in a large-scale setting, which includes possibly simple nonsmooth convex regularizer and simple convex set constraints. By reformulating GLP as an equivalent convex-concave min-max problem, we show that the linear structure in the problem can be used to design an efficient, scalable first-order algorithm, to which we give the name \emph{Coordinate Linear Variance Reduction} (\textsc{clvr}; pronounced "clever"). \textsc{clvr} is an incremental coordinate method with implicit variance reduction that outputs an \emph{affine combination} of the dual variable iterates. \textsc{clvr} yields improved complexity results for (GLP) that depend on the max row norm of the linear constraint matrix in (GLP) rather than the spectral norm. When the regularization terms and constraints are separable, \textsc{clvr} admits an efficient lazy update strategy that makes its complexity bounds scale with the number of nonzero elements of the linear constraint matrix in (GLP) rather than the matrix dimensions. We show that Distributionally Robust Optimization (DRO) problems with ambiguity sets based on both $f$-divergence and Wasserstein metrics can be reformulated as (GLPs) by introducing sparsely connected auxiliary variables. We complement our theoretical guarantees with numerical experiments that verify our algorithm's practical effectiveness, both in terms of wall-clock time and number of data passes.

Variance Reduction via Primal-Dual Accelerated Dual Averaging for Nonsmooth Convex Finite-Sums

We study structured nonsmooth convex finite-sum optimization that appears widely in machine learning applications, including support vector machines and least absolute deviation. For the primal-dual formulation of this problem, we propose a novel algorithm called \emph{Variance Reduction via Primal-Dual Accelerated Dual Averaging (\vrpda)}. In the nonsmooth and general convex setting, \vrpda~has the overall complexity $O(nd\log\min \{1/\epsilon, n\} + d/\epsilon )$ in terms of the primal-dual gap, where $n$ denotes the number of samples, $d$ the dimension of the primal variables, and $\epsilon$ the desired accuracy. In the nonsmooth and strongly convex setting, the overall complexity of \vrpda~becomes $O(nd\log\min\{1/\epsilon, n\} + d/\sqrt{\epsilon})$ in terms of both the primal-dual gap and the distance between iterate and optimal solution. Both these results for \vrpda~improve significantly on state-of-the-art complexity estimates, which are $O(nd\log \min\{1/\epsilon, n\} + \sqrt{n}d/\epsilon)$ for the nonsmooth and general convex setting and $O(nd\log \min\{1/\epsilon, n\} + \sqrt{n}d/\sqrt{\epsilon})$ for the nonsmooth and strongly convex setting, in a much more simple and straightforward way. Moreover, both complexities are better than \emph{lower} bounds for general convex finite sums that lack the particular (common) structure that we consider. Our theoretical results are supported by numerical experiments, which confirm the competitive performance of \vrpda~compared to state-of-the-art.

Fast Cyclic Coordinate Dual Averaging with Extrapolation for Generalized Variational Inequalities

We propose the \emph{Cyclic cOordinate Dual avEraging with extRapolation (CODER)} method for generalized variational inequality problems. Such problems are fairly general and include composite convex minimization and min-max optimization as special cases. CODER is the first cyclic block coordinate method whose convergence rate is independent of the number of blocks, which fills the significant gap between cyclic coordinate methods and randomized ones that remained open for many years. Moreover, CODER provides the first theoretical guarantee for cyclic coordinate methods for solving generalized variational inequality problems under only monotonicity and Lipschitz continuity assumptions. To remove the dependence on the number of blocks, the analysis of CODER is based on a novel Lipschitz condition with respect to a Mahalanobis norm rather than the commonly used coordinate-wise Lipschitz condition; to be applicable to general variational inequalities, CODER leverages an extrapolation strategy inspired by the recent developments in primal-dual methods. Our theoretical results are complemented by numerical experiments, which demonstrate competitive performance of CODER compared to other coordinate methods.

Stochastic Variance Reduction via Accelerated Dual Averaging for Finite-Sum Optimization

In this paper, we introduce a simplified and unified method for finite-sum convex optimization, named \emph{Stochastic Variance Reduction via Accelerated Dual Averaging (SVR-ADA)}. In the nonstrongly convex and smooth setting, SVR-ADA can attain an $O\big(\frac{1}{n}\big)$-accurate solution in $O(n\log\log n)$ number of stochastic gradient evaluations, where $n$ is the number of samples; meanwhile, SVR-ADA matches the lower bound of this setting up to a $\log\log n$ factor. In the strongly convex and smooth setting, SVR-ADA matches the lower bound in the regime $n\le O(\kappa)$ while it improves the rate in the regime $n\gg \kappa$ to $O(n\log\log n +\frac{n\log(1/(n\epsilon))}{\log(n/\kappa)})$, where $\kappa$ is the condition number. SVR-ADA improves complexity of the best known methods without use of any additional strategy such as optimal black-box reduction, and it leads to a unified convergence analysis and simplified algorithm for both the nonstrongly convex and strongly convex settings. Through experiments on real datasets, we also show the superior performance of SVR-ADA over existing methods for large-scale machine learning problems.

Learning Diverse and Discriminative Representations via the Principle of Maximal Coding Rate Reduction

To learn intrinsic low-dimensional structures from high-dimensional data that most discriminate between classes, we propose the principle of Maximal Coding Rate Reduction ($\text{MCR}^2$), an information-theoretic measure that maximizes the coding rate difference between the whole dataset and the sum of each individual class. We clarify its relationships with most existing frameworks such as cross-entropy, information bottleneck, information gain, contractive and contrastive learning, and provide theoretical guarantees for learning diverse and discriminative features. The coding rate can be accurately computed from finite samples of degenerate subspace-like distributions and can learn intrinsic representations in supervised, self-supervised, and unsupervised settings in a unified manner. Empirically, the representations learned using this principle alone are significantly more robust to label corruptions in classification than those using cross-entropy, and can lead to state-of-the-art results in clustering mixed data from self-learned invariant features.

Towards Unified Acceleration of High-Order Algorithms under Hölder Continuity and Uniform Convexity

In this paper, through a very intuitive {\em vanilla proximal method} perspective, we derive accelerated high-order optimization algorithms for minimizing a convex function that has H\"{o}lder continuous derivatives. In this general convex setting, we propose a {\em unified acceleration algorithm} with an iteration complexity that matches the lower iteration complexity bound given in \cite{grapiglia2019tensor}. If the function is further uniformly convex, we propose a {\em general restart scheme}. The iteration complexity of the algorithm matches existing lower bounds in most important cases. For practical implementation, we introduce a new and effective heuristic that significantly simplifies the binary search procedure required by the algorithm, which makes the algorithm in general settings as efficient as the special case \cite{grapiglia2019tensor}. On large-scale classification datasets, our algorithm demonstrates clear and consistent advantages of high-order acceleration methods over first-order ones, in terms of run-time complexity. Our formulation considers the more general composite setting in which the objective function may contain a second possibly non-smooth convex term. Our analysis and proofs are also applicable to the general case in which the high-order smoothness conditions are with respect to non-Euclidean norms.