VICON: Vision In-Context Operator Networks for Multi-Physics Fluid Dynamics Prediction

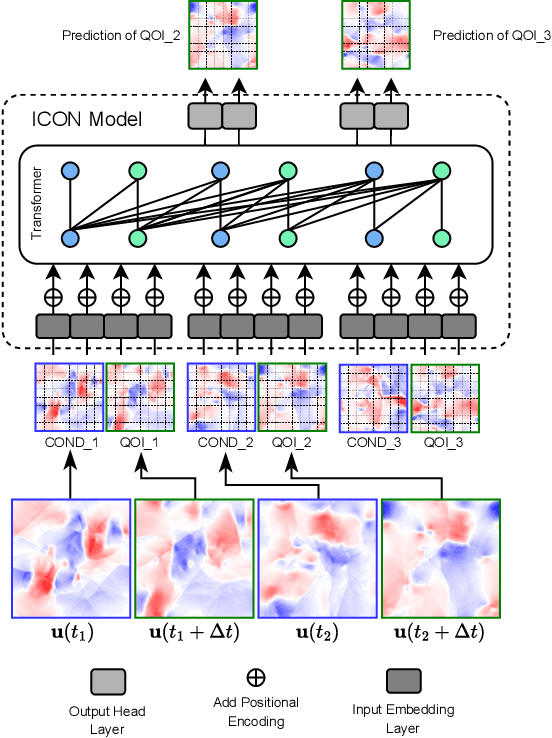
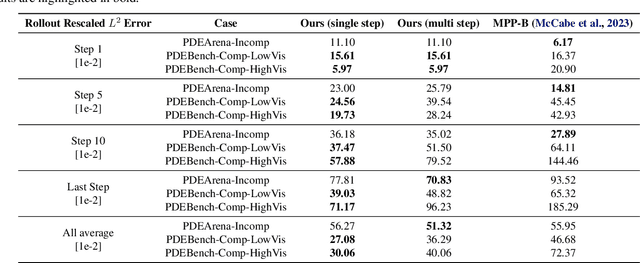
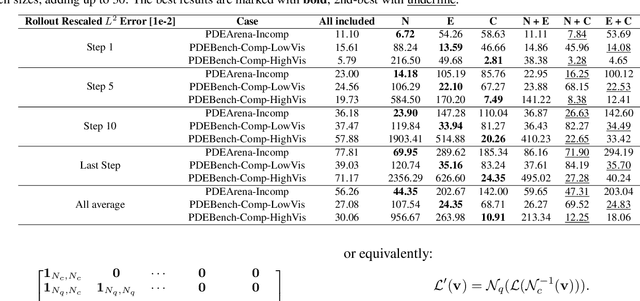
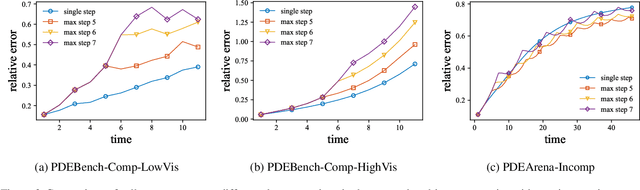
In-Context Operator Networks (ICONs) are models that learn operators across different types of PDEs using a few-shot, in-context approach. Although they show successful generalization to various PDEs, existing methods treat each data point as a single token, and suffer from computational inefficiency when processing dense data, limiting their application in higher spatial dimensions. In this work, we propose Vision In-Context Operator Networks (VICON), incorporating a vision transformer architecture that efficiently processes 2D functions through patch-wise operations. We evaluated our method on three fluid dynamics datasets, demonstrating both superior performance (reducing scaled $L^2$ error by $40\%$ and $61.6\%$ for two benchmark datasets for compressible flows, respectively) and computational efficiency (requiring only one-third of the inference time per frame) in long-term rollout predictions compared to the current state-of-the-art sequence-to-sequence model with fixed timestep prediction: Multiple Physics Pretraining (MPP). Compared to MPP, our method preserves the benefits of in-context operator learning, enabling flexible context formation when dealing with insufficient frame counts or varying timestep values.

Graph Fourier Neural ODEs: Bridging Spatial and Temporal Multiscales in Molecular Dynamics

Molecular dynamics simulations are crucial for understanding complex physical, chemical, and biological processes at the atomic level. However, accurately capturing interactions across multiple spatial and temporal scales remains a significant challenge. We present a novel framework that jointly models spatial and temporal multiscale interactions in molecular dynamics. Our approach leverages Graph Fourier Transforms to decompose molecular structures into different spatial scales and employs Neural Ordinary Differential Equations to model the temporal dynamics in a curated manner influenced by the spatial modes. This unified framework links spatial structures with temporal evolution in a flexible manner, enabling more accurate and comprehensive simulations of molecular systems. We evaluate our model on the MD17 dataset, demonstrating consistent performance improvements over state-of-the-art baselines across multiple molecules, particularly under challenging conditions such as irregular timestep sampling and long-term prediction horizons. Ablation studies confirm the significant contributions of both spatial and temporal multiscale modeling components. Our method advances the simulation of complex molecular systems, potentially accelerating research in computational chemistry, drug discovery, and materials science.

Adapting While Learning: Grounding LLMs for Scientific Problems with Intelligent Tool Usage Adaptation

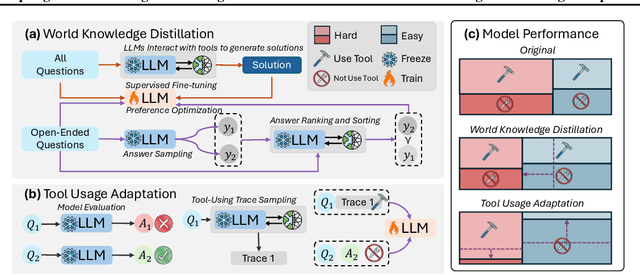
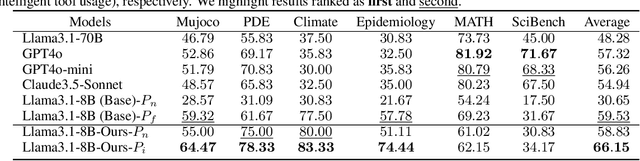
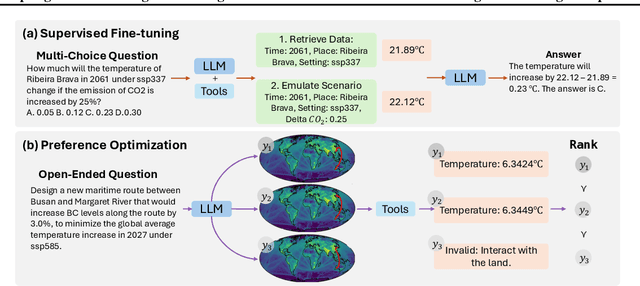
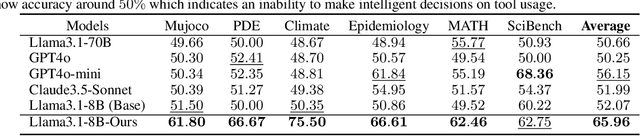
Large Language Models (LLMs) demonstrate promising capabilities in solving simple scientific problems but often produce hallucinations for complex ones. While integrating LLMs with tools can increase reliability, this approach typically results in over-reliance on tools, diminishing the model's ability to solve simple problems through basic reasoning. In contrast, human experts first assess problem complexity using domain knowledge before choosing an appropriate solution approach. Inspired by this human problem-solving process, we propose a novel two-component fine-tuning method. In the first component World Knowledge Distillation (WKD), LLMs learn directly from solutions generated using tool's information to internalize domain knowledge. In the second component Tool Usage Adaptation (TUA), we partition problems into easy and hard categories based on the model's direct answering accuracy. While maintaining the same alignment target for easy problems as in WKD, we train the model to intelligently switch to tool usage for more challenging problems. We validate our method on six scientific benchmark datasets, spanning mathematics, climate science and epidemiology. On average, our models demonstrate a 28.18% improvement in answer accuracy and a 13.89% increase in tool usage precision across all datasets, surpassing state-of-the-art models including GPT-4o and Claude-3.5.

Physics-Informed Regularization for Domain-Agnostic Dynamical System Modeling

Learning complex physical dynamics purely from data is challenging due to the intrinsic properties of systems to be satisfied. Incorporating physics-informed priors, such as in Hamiltonian Neural Networks (HNNs), achieves high-precision modeling for energy-conservative systems. However, real-world systems often deviate from strict energy conservation and follow different physical priors. To address this, we present a framework that achieves high-precision modeling for a wide range of dynamical systems from the numerical aspect, by enforcing Time-Reversal Symmetry (TRS) via a novel regularization term. It helps preserve energies for conservative systems while serving as a strong inductive bias for non-conservative, reversible systems. While TRS is a domain-specific physical prior, we present the first theoretical proof that TRS loss can universally improve modeling accuracy by minimizing higher-order Taylor terms in ODE integration, which is numerically beneficial to various systems regardless of their properties, even for irreversible systems. By integrating the TRS loss within neural ordinary differential equation models, the proposed model TREAT demonstrates superior performance on diverse physical systems. It achieves a significant 11.5% MSE improvement in a challenging chaotic triple-pendulum scenario, underscoring TREAT's broad applicability and effectiveness.

DELTA: Dual Consistency Delving with Topological Uncertainty for Active Graph Domain Adaptation

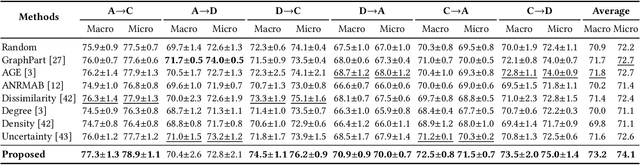
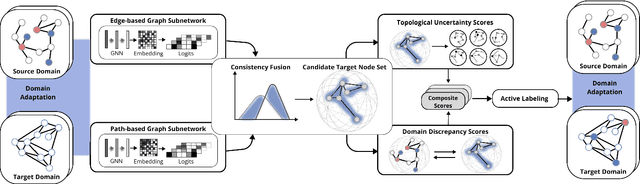
Graph domain adaptation has recently enabled knowledge transfer across different graphs. However, without the semantic information on target graphs, the performance on target graphs is still far from satisfactory. To address the issue, we study the problem of active graph domain adaptation, which selects a small quantitative of informative nodes on the target graph for extra annotation. This problem is highly challenging due to the complicated topological relationships and the distribution discrepancy across graphs. In this paper, we propose a novel approach named Dual Consistency Delving with Topological Uncertainty (DELTA) for active graph domain adaptation. Our DELTA consists of an edge-oriented graph subnetwork and a path-oriented graph subnetwork, which can explore topological semantics from complementary perspectives. In particular, our edge-oriented graph subnetwork utilizes the message passing mechanism to learn neighborhood information, while our path-oriented graph subnetwork explores high-order relationships from substructures. To jointly learn from two subnetworks, we roughly select informative candidate nodes with the consideration of consistency across two subnetworks. Then, we aggregate local semantics from its K-hop subgraph based on node degrees for topological uncertainty estimation. To overcome potential distribution shifts, we compare target nodes and their corresponding source nodes for discrepancy scores as an additional component for fine selection. Extensive experiments on benchmark datasets demonstrate that DELTA outperforms various state-of-the-art approaches.

Recent Advances on Machine Learning for Computational Fluid Dynamics: A Survey

This paper explores the recent advancements in enhancing Computational Fluid Dynamics (CFD) tasks through Machine Learning (ML) techniques. We begin by introducing fundamental concepts, traditional methods, and benchmark datasets, then examine the various roles ML plays in improving CFD. The literature systematically reviews papers in recent five years and introduces a novel classification for forward modeling: Data-driven Surrogates, Physics-Informed Surrogates, and ML-assisted Numerical Solutions. Furthermore, we also review the latest ML methods in inverse design and control, offering a novel classification and providing an in-depth discussion. Then we highlight real-world applications of ML for CFD in critical scientific and engineering disciplines, including aerodynamics, combustion, atmosphere & ocean science, biology fluid, plasma, symbolic regression, and reduced order modeling. Besides, we identify key challenges and advocate for future research directions to address these challenges, such as multi-scale representation, physical knowledge encoding, scientific foundation model and automatic scientific discovery. This review serves as a guide for the rapidly expanding ML for CFD community, aiming to inspire insights for future advancements. We draw the conclusion that ML is poised to significantly transform CFD research by enhancing simulation accuracy, reducing computational time, and enabling more complex analyses of fluid dynamics. The paper resources can be viewed at https://github.com/WillDreamer/Awesome-AI4CFD.

TANGO: Time-Reversal Latent GraphODE for Multi-Agent Dynamical Systems

Learning complex multi-agent system dynamics from data is crucial across many domains, such as in physical simulations and material modeling. Extended from purely data-driven approaches, existing physics-informed approaches such as Hamiltonian Neural Network strictly follow energy conservation law to introduce inductive bias, making their learning more sample efficiently. However, many real-world systems do not strictly conserve energy, such as spring systems with frictions. Recognizing this, we turn our attention to a broader physical principle: Time-Reversal Symmetry, which depicts that the dynamics of a system shall remain invariant when traversed back over time. It still helps to preserve energies for conservative systems and in the meanwhile, serves as a strong inductive bias for non-conservative, reversible systems. To inject such inductive bias, in this paper, we propose a simple-yet-effective self-supervised regularization term as a soft constraint that aligns the forward and backward trajectories predicted by a continuous graph neural network-based ordinary differential equation (GraphODE). It effectively imposes time-reversal symmetry to enable more accurate model predictions across a wider range of dynamical systems under classical mechanics. In addition, we further provide theoretical analysis to show that our regularization essentially minimizes higher-order Taylor expansion terms during the ODE integration steps, which enables our model to be more noise-tolerant and even applicable to irreversible systems. Experimental results on a variety of physical systems demonstrate the effectiveness of our proposed method. Particularly, it achieves an MSE improvement of 11.5 % on a challenging chaotic triple-pendulum systems.

Bi-Stride Multi-Scale Graph Neural Network for Mesh-Based Physical Simulation

Learning physical systems on unstructured meshes by flat Graph neural networks (GNNs) faces the challenge of modeling the long-range interactions due to the scaling complexity w.r.t. the number of nodes, limiting the generalization under mesh refinement. On regular grids, the convolutional neural networks (CNNs) with a U-net structure can resolve this challenge by efficient stride, pooling, and upsampling operations. Nonetheless, these tools are much less developed for graph neural networks (GNNs), especially when GNNs are employed for learning large-scale mesh-based physics. The challenges arise from the highly irregular meshes and the lack of effective ways to construct the multi-level structure without losing connectivity. Inspired by the bipartite graph determination algorithm, we introduce Bi-Stride Multi-Scale Graph Neural Network (BSMS-GNN) by proposing \textit{bi-stride} as a simple pooling strategy for building the multi-level GNN. \textit{Bi-stride} pools nodes by striding every other BFS frontier; it 1) works robustly on any challenging mesh in the wild, 2) avoids using a mesh generator at coarser levels, 3) avoids the spatial proximity for building coarser levels, and 4) uses non-parametrized aggregating/returning instead of MLPs during pooling and unpooling. Experiments show that our framework significantly outperforms the state-of-the-art method's computational efficiency in representative physics-based simulation cases.